1. 背景
目前各个安全厂商都开始积极地挖掘情报数据的价值,研究威胁情报分析与共享技术。越来越多的安全厂商开始提供威胁情报服务,众多企业的安全应急响应中心也开始接收威胁情报,威胁情报的受重视程度日益变高。根据SANS 发布的全球企业的威胁情报调查报告(The SANS State of Cyber Threat Intelligence Survey: CTI Important and Maturing),94% 的受访企业表示目前已有威胁情报项目,70% 企业采了用威胁情报供应商的商业源。
依托腾讯近20年的安全能力建设和安全实践经验,依托覆盖全网海量安全大数据,大约每日2万亿安全日志,通过数据归一、清洗、建模、分类、知识图谱化,快速的跟踪和识别出海量数据中威胁要素,依托腾讯强大的机器学习平台和专业的安全运营能力,将威胁要素生产运营成实时有效,具有丰富上下文信息的威胁情报。
目前腾讯威胁情报的自产率占整体情报的90%,跟踪了全网超3000个黑灰产团伙,近百个APT组织。其中一系列关键技术就是从海量数据中进行恶意域名的挖掘及家族的识别,本文将对图分析技术在恶意域名和家族恶意域名挖掘的应用进行详细介绍。
2. 恶意域名挖掘简介
上一篇文章《腾讯安全威胁情报中心“明厨亮灶”工程:自动化恶意域名检测揭密》介绍了一种利用有监督的机器学习模型检测恶意域名的方法。本文将介绍一种基于图分析技术的半监督和无监督的恶意域名挖掘算法。本方法不仅能够识别恶意域名,进一步还能够挖掘恶意家族域名。
图模型能够很好表示安全实体与实体之间的关联关系,在图模型中可以作相关概率推导或者图挖掘方法。本文主要利用图模型中的两种方法挖掘恶意域名:概率图模型和图聚类算法。概率图模型(Probability Graphic Model,PGM)是机器学习中一个重要的分支,把变量建模成图节点,关系建模成图的边。通过观察变量(observed state)已经关系推导出未知变量状态的概率。概率图模型成功应用于医学、图像处理等领域。概率图模型分为两种,一种是有向图模型,又称为贝叶斯模型,另一种是无向图模型,又称为马尔科夫网络。图聚类是利用图的关系对图的节点按照节点之间紧密程度划分成不同的类簇。
本文首先利用海量数据构造图,把域名关系建模成图模型:1)使用图推导(Graph Inference)推断恶意域名为恶意的概率;2)利用无监督的图聚类方法挖掘家族恶意域名。
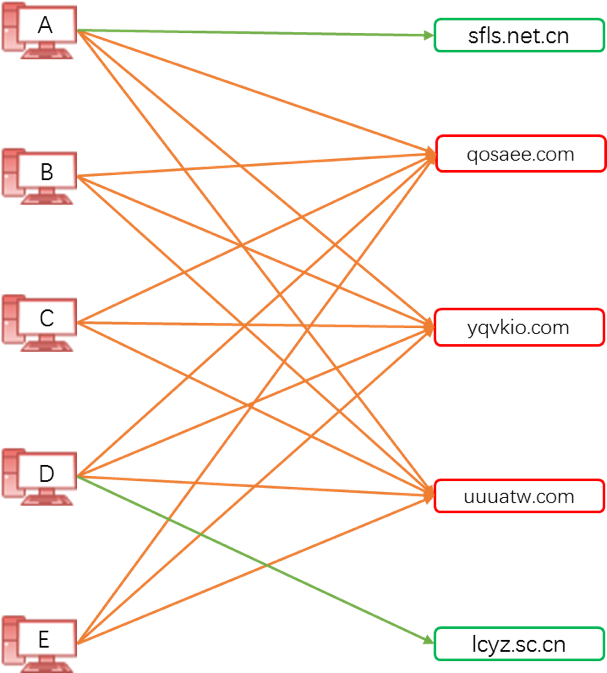
利用域名数据,构建主机与域名的访问关系二分图。如果蜜罐主机H发起了域名D的DNS请求,在域名-主机二分图添加一条边连接主机H与域名D。如果两个域名D1和D2属于相同家族F,那么感染家族F的主机很高概率会同时访问家族F的域名D1和D2。感染相同家族的主机会访问相同家族的C2域名,相同家族的C2域名会被感染主机同时访问。根据Guilt by association的理论,如果一个主机访问了恶意域名,那么这个主机访问的域名是恶意的概率会变得更高。并且感染相同家族的主机会访问相同家族的C2域名,相同家族的C2域名会被感染主机同时访问。 如图 1所示,中间三个红色域名是相同家族域名,绿色域名表示两个高中学校官方网站;左边5台红色主机表示感染了该家族恶意软件的主机。从概率上来说,红色域名被5台主机同时访问的概率较高。而两个绿色域名在随机条件下同时被大量主机访问的概率较低。因此可以用域名的共同访问主机数量来衡量域名关系的强度。假设访问域名d1的主机集合为S1,访问域名d2的主机集合为S2,如果S1与S2的交集包含元素越多说明d1和d2的关系越紧密。除白名单域名以外,例如,google.com、qq.com、baidu.com、taobao.com等著名域名,通常情况下大部分主机都访问这些著名域名,其交集包含元素非常多,而这类域名对挖掘恶意域名并没有影响。在处理时需要对数据降噪。
处理域名与域名关系时,使用交集包含的元素数量并不十分合理。如果使用交集,域名关系强度会被域名访问频次占主导,恶意域名访问频次并不总是高频次,此外,如果交集,在计算时必须两两计算,计算开销巨大。因此本文使用Jaccard Similarity更为合理,这样能够把不同广度域名用一种方式衡量。集合A与集合B的Jaccard Similarity定义为:

那么域名d1和d2的关系,可以定义为:

其中S1是访问域名d1的主机集合,S2是访问域名d2的主机集合。

域名数量有千万级别,如果要计算所有域名对的Jaccard相似度,计算复杂度是百万亿级,且可扩展性比较差。如果非要计算所有域名两两之间的Jaccard相似度,则没有任何办法去提升计算效率。但如果只关心那些Jaccard相似度较高的域名对,而jaccard相似度很低的域名对没有必要关联起来。那么局部敏感哈希(Local Sensitive Hashing,LSH)算法可以大幅提升计算效率并保留域名的关联性。
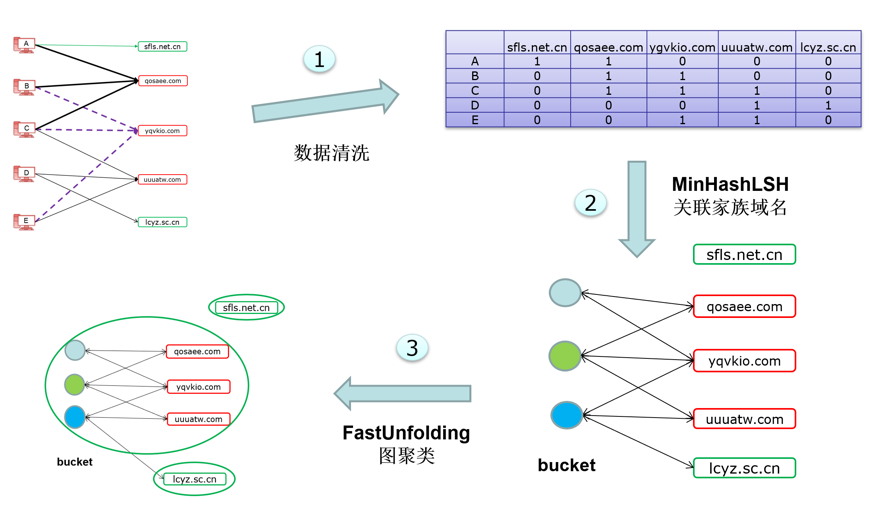
使用局部敏感哈希算法把域名映射到哈希桶,在同一个哈希桶的域名,它们的Jaccard相似度较高。把域名-主机访问关系二分图通过LSH算法转换成domain-bucket二分图。根据LSH算法的特点,域名与域名的Jaccard相似度越高,它们会以高概率落到更多的哈希桶,域名关系可以通过bucket的数量来衡量。方法流程如图 2所示,利用少量已知的恶意域名和正常域名,使用Belief propagation算法推导domain-bucket二分图上未知域名为恶意的概率。除了对domain-bucket二分图做概率推导,还可以对domain-bucket做无监督的图聚类方法,聚类结果可以作为相同家族的恶意域名。无监督聚类方法流程如图 3所示。
3. 方法详细描述
二分图转换——MinHashing与LSH算法
域名-主机二分图非常稀疏,域名与域名的关系如果不经过主机的“好坏”信息,恶意域名的标签很难通过稀疏二分图传播到未知域名。此外,要根据少量已知的恶意域名和白名单域名,在稀疏图中推导未知恶意域名为恶意概率非常困难。
因此把域名-主机二分图转换成domain-bucket二分图。
A. MinHashing
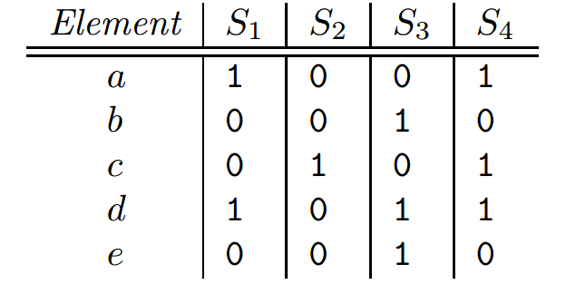
有四个集合,分别有S1、S2、S3、S4,这里可以看做是四个域名,集合有5个元素,这里可以认为是5个域名a、b、c、d、e。域名a和d访问了S1域名,依次类推。domain-host的关系可以用矩阵来表示,如图 4所示,4个域名5台主机的关系矩阵,在真实环境中domain-host关系矩阵大约为千万级*亿级的矩阵。
MinHashing的目的是找到集合的签名,但是又得保持集合两两之间的相似性。
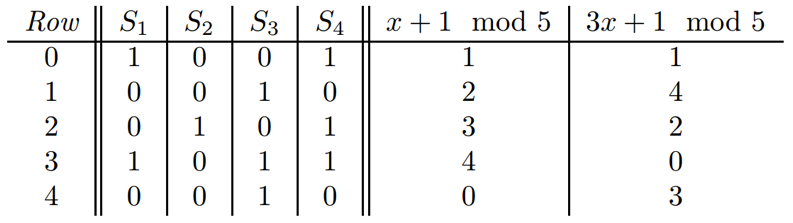
对行重新排列(repermutation),得到一个新的矩阵关系,重排后的关系矩阵与原始关系矩阵表示的内容完全一致。如图 5所示

Minhashing对重排的关系矩阵做一个简单的哈希,哈希值是排列的第一个“出现的”域名。h(S1) = a, h(S2) = c, h(S3) = b, h(S4) = a。可以证明任意两个集合的哈希值相同的概率等于这两个集合的Jaccard相似度(证明参考Mining of Massive Datasets[2])。因此使用多个排列并取其哈希值则可以作为集合的签名。

通常情况下使用几百个哈希表示集合的签名,签名保持了集合的Jaccard相似度的特性。如果域名相似度越高,签名相同元素越多。
集合使用minhashing签名表示虽然更简单,但是如果使用暴力算法计算集合之间的Jaccard相似度还是需要平方级别复杂度。因此,为了能够较大概率把相似度较高的集合找到,需要用到LSH算法。
B. 局部敏感哈希算法
局部敏感哈希算法能够把Jaccard相似度较高的域名映射到一个bucket中,获取相似域名只需要在同一个bucket中寻找即可,不需要对所有集合两两计算,大幅降低了相似域名的计算负责度。

如表 1所示,包含3个域名d1,d2,d3,包含6个Minhashing的签名,表中出现了8台主机h1, …, h8,把6个minhashing值分成3个band,每个band包含两个hash值。每一个band中,该band里所有的minhashing值相同(也可以用哈希函数替代)则放到同一个bucket中。
如表 1所示,band3中d2和d3的两个minhashing都是h7与h6,因此d2和d3在相同的bucket中,d1则单独在一个bucket中。需要说明,不同的band中计算哈希可以用相同的哈希算法,但是需要不同的bucket,即不同band,如果minhashing相同也不会映射到同一个bucket。如果存在一个bucket包含两个域名,那么这两个域名的相似度则不会漏掉。
只要域名相似度概率大于一定阈值,则这两个域名至少会落在某个bucket中,被取出来,为什么?

因此可以调整r和b来调整期望的召回率(期望Jaccard相似度大于多少的时候能够捕获到这样的域名对)

详细的minhashing与LSH算法参考Mining of Massive Datasets[2]
C. 构建domain-bucket二分图
通过局部敏感哈希算法把域名映射到相同的bucket中,如何构建域名与域名的关系图呢?两种选择,一种是域名与域名直接相连的图,只要存在两个域名存在于某一个bucket中,则添加一条边。构成一个域名与域名相互连接的图;另一种是构建二分图,一边为域名,另一边为bucket。如果域名存在于某个bucket,则相应域名和bucket添加一条边。构造的domain-bucket二分图有两方面特点:1)相似度大的域名通过bucket关联(同家族高概率关联);2)相似度小的域名无关联(不同家族低概率关联)
本方法选择第二种方式构建二分图,如图 3所示。因为第一种构建方法复杂度高;第二种方法能够通过bucket间接关联相似度高的域名。能够间接从已知域名推导未知域名。也能够通过图聚类方法挖掘家族恶意域名。
D. 执行度传播算法(Belief Propagation)
置信度传播算法是一种近似计算非观察变量概率的算法。domain-bucket二分图是无向图,域名有两个状态(malicious或者benign),bucket也有两个状态。如果域名为恶意,那么这个域名所在的bucket为恶意的概率会相应增加;如果bucket的状态为“恶意”,那么bucket所连接的域名为恶意的概率相应增加。
置信度传播算法在线性时间复杂度内近似估计了未观察变量(未知域名)的边缘概率分布。能够有效计算未知域名为恶意的概率。
具体置信度传播算法参考[3]
E. 图聚类算法
Fast unfolding算法是一种层次贪心算法优化图的模块度。模块度也称模块化度量值,是目前常用的一种衡量网络社区结构强度的方法。模块度定义如下:



该算法包括两个阶段并不停重复这两个阶段直到算法收敛:
第一阶段合并社区,算法将每个结点当作一个社区,基于模块度增量最大化标准决定你哪些邻居社区应该被合并。经过一轮扫描后开始第二阶段,算法将第一阶段发现的所有社区重新看成结点,构建新的网络,在新网络上重复进行第一阶段,这两个阶段重复运行,直到网络社区划分的模块度不再增长,得到网络的社区近似最优划分。
这个简单算法具有一下两方面优点:
1) 算法的步骤比较直观并且易于实现,时间复杂度低
2) 算法不需要提前设定网络的社区数,并且该算法可以呈现网络的完整的分层社区结构,能够发现在线社交网络的分层的虚拟社区结构,获得不同分辨率的虚拟社区;不需要提前设定社区数这一点在比较重,因为我们根本无法提前知道所抽取的子图有多少个社团
F. 参数选择
局部敏感哈希算法需要确定Jaccard相似度大于多少位相似的域名。由于主机访问域名的稀疏性,大部分主机除了共同域名会访问较大量其他的域名。因此Jaccard similarity不会非常高,因此设定jaccard similarity大于0.25左右的时候就认为是相似的域名。根据jaccard similarity阈值选择相应的band数目以及每个band的minhashing数量。选择band b数为150,每个band数r为4。jaccard相似度s与至少存在同一个bucket的概率的关系如图 10所示。

G. 过滤domain-bucket图
因为置信度传播算法需要从已知域名(观察变量,observed variable)推导(计算边缘概率,marginal probability)未知域名(未观察变量,unobserved variable)为恶意的概率。在domain-bucket二分图中,如果一个连通分量仅仅包含未知域名或者仅仅包含已知域名,那么这个连通分量不会推导出任何有意义的数据,过滤掉这样的节点。
4. 发现的恶意域名
本方法主要能够发现以下几类:
A. Mykings的dga家族,mykings家族的dga大约1个月生成一次,一次大约100个左右,tld包括pw等。
B. 多种已知僵尸网络家族,如dorkbot、virut、chinad、conficker等
C. 色情、菠菜网站,动态域名。由于色情和菠菜网站用户基本固定,并且色情网站为了逃逸黑名单检测,经常更换站点域名
D. 通过概率图模型的方法,把御见威胁情报中的域名,作为种子,每天推导发现与这些相关联的恶意域名。
E. 噪声,由于随机访问的关系,聚类不总是聚类出来都是同一个家族或者强关联的,这一部分数据需要进一步通过安全规则进行去噪,例如访问文件、解析域名等关系进一步确认。
5. 方法优缺点及其改进方向
方案优缺点:
通过概率图模型建模域名与域名的关系,通过已知域名的“好坏”推导未知域名“好坏”的概率。这种方法能够有效地从数据集中通过少量已知域名推导关联域名的“好坏”。能够有效地识别恶意软件连接控制服务器域名的变种。
但是这种方法也存在一定缺陷,如果一个连通分量没有标记域名,则这个连通分量里的所有未知域名算法不能够感知到。
未来恶意域名分析点:
domain-host转为为domain-bucket的方法是通过共同访问主机比例衡量域名与域名之间的关系。此外,还可以通过域名解析到的IP地址来衡量域名与域名的关系。

[1] Guilt by Association: Large Scale Malware Detection by Mining File-relation Graphs
[2] http://www.mmds.org
[3] Factor Graphs and the sum-product Algorithm
[4] Blondel V D, Guillaume J L, Lambiotte R;. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics: Theory and Experiment. 2008