下面以最经典的AlexNet模型为例子,计算感受野,模型计算量和大小(内存)。下面这张图是AlexNet的结构图,看起来比较直观。
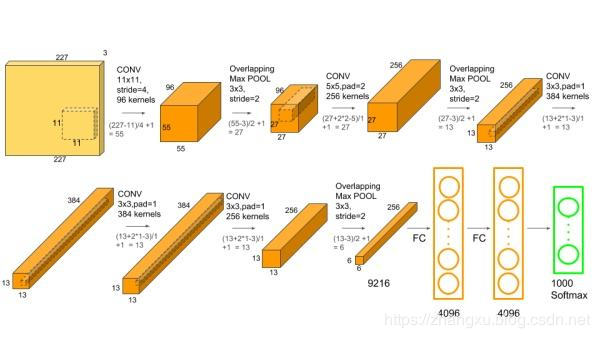
感受野
感受野是检测和分割任务中比较重要的指标,它是一个逐层叠加的过程,计算到最后一层的卷积特征图输出上,它的计算公式是:
RFi=RFi−1+(kernelsize−1)×stride,RF0=1RF_{i}=RF_{i-1}+(kernelsize-1)\times stride,RF_{0}=1RFi=RFi−1+(kernelsize−1)×stride,RF0=1
其中RF0RF_{0}RF0默认是输入层,感受野为1。所以AlexNet的感受野计算为:
- 第一层,卷积:RF1=1+(11−1)×4=41RF_{1}=1+(11-1)\times 4=41RF1=1+(11−1)×4=41
- 第二层,池化:RF2=41+(3−1)×2=45RF_{2}=41+(3-1)\times 2=45RF2=41+(3−1)×2=45
- 第三层,卷积:RF3=45+(5−1)×2=53RF_{3}=45+(5-1)\times 2=53RF3=45+(5−1)×2=53
- 第四层,池化:RF2=53+(3−1)×2=57RF_{2}=53+(3-1)\times 2=57RF2=53+(3−1)×2=57
- 第五层,卷积:RF2=57+(3−1)×1=59RF_{2}=57+(3-1)\times 1=59RF2=57+(3−1)×1=59
- 第六层,卷积:RF2=59+(3−1)×1=61RF_{2}=59+(3-1)\times 1=61RF2=59+(3−1)×1=61
- 第七层,卷积:RF2=61+(3−1)×1=63RF_{2}=61+(3-1)\times 1=63RF2=61+(3−1)×1=63
- 第八层,池化:RF2=63+(3−1)×2=67RF_{2}=63+(3-1)\times 2=67RF2=63+(3−1)×2=67
第八层的输出就是6×6×2566\times6\times2566×6×256,感受野的计算就结束了。
计算量
计算量是评价一个模型重要的标准之一,其实在模型的计算量统计时有两点简化的地方:
- 模型的不同层中,卷积层和全连接层是占据了绝大多数的计算量,所以下面我们只关注这两个层的计算;
- 卷积层和全连接层都有对应的“+”操作,而这些“+”操作也被忽略掉了(一般情况下,是忽略“+”操作的,但是也会有例外,比如YOLOv3在计算主干网络算力的时候)。
卷积层
对于一个w1×h1×c1w_{1}\times h_{1}\times c_{1}w1×h1×c1的输入特征图,经过3×33\times33×3的卷积核,输出w2×h2×c2w_{2}\times h_{2}\times c_{2}w2×h2×c2的特征图,那么卷积一次将输出一个值,计算量为:
Fo=3×3×c1+1F_{o}=3\times3\times c_{1}+1Fo=3×3×c1+1
其中这个1是每个卷积核对应的偏置,它也要做一次乘运算,然后,卷积完一张特征图w2×h2w_{2}\times h_{2}w2×h2计算量为:
Fc=Fo×w2×h2F_{c}=F_{o}\times w_{2}\times h_{2}Fc=Fo×w2×h2
最后需要c2c_{2}c2个卷积核才能完成w2×h2×c2w_{2}\times h_{2}\times c_{2}w2×h2×c2的输出:
Fa=Fc×c2F_{a}=F_{c}\times c_{2}Fa=Fc×c2
全连接层
全连接层的计算量分析就更简单了,因为它没有滑动,就只输入相乘相加为一个输出,假设输出维度为o1o_{1}o1,输出维度为o2o_{2}o2,那么计算量为:
F=(o1+1)×o2F=(o_{1}+1)\times o_{2}F=(o1+1)×o2
AlexNet逐层计算计算量的话太多了,下面偷个懒,只算下第一层举个例子吧。

这是AlexNet的的参数数量和计算量分布图,第一层卷积的计算量是105M FLOPs,FLOPs是“每秒浮点运算次数”,在作为计算量是,就是浮点运算次数,那么105MFLOPs就应该是105×106105\times10^6105×106次浮点运算。
套用上面公式就是:
(11×11×3+1)×55×55×96=105705600=105M(11\times11\times3+1)\times55\times55\times96= 105705600=105M (11×11×3+1)×55×55×96=105705600=105M
模型大小
模型的大小完全由模型的参数数量和参数的存储形式决定:
卷积层
卷积层的参数数量就是一个卷积核的参数乘上卷积核的个数:
Pn=(w×h×ci+1)×coP_{n}=(w\times h\times c_{i}+1)\times c_{o}Pn=(w×h×ci+1)×co
www,hhh和 c_{i}是卷积核的尺寸,coc_{o}co是卷积核个数,也就是输出通道数,1是偏置。
全连接层
全连接层的参数数量输入输出的神经元连接的那个权重:
Pn=(o1+1)×o2P_{n}=(o_{1}+1)\times o_{2}Pn=(o1+1)×o2
o1o_{1}o1是输入神经元个数,和o2o_{2}o2是输出神经元个数,1是偏置。
AlexNet的参数数量由60M个,也就是六千万个,参数只在卷积层和全连接层出现,下面还是只计算第一层卷积的参数:
96×11×11×3+96=34944=35K96\times11\times11\times3+96=34944=35K96×11×11×3+96=34944=35K
最后还剩下一个转换就是参数的数量,怎么转成存储的大小,一般情况下模型的参数是按照float形式存储的,占4个字节,AlexNet模型大小是238147KB:
60M×4=240000000B=234375KB60M\times4=240000000B=234375KB60M×4=240000000B=234375KB
因为60M这个数是一个约等,所以计算出来是234375KB,而实际上是238147KB。