小云今年大三在一家互联网公司实习,今天下班回到寝室闷闷不乐,小帅见状关心到:怎么了?碰到什么不开心的事了吗?
小云叹了口气:今天我写的程序中涉及到小数计算,出了个bug,被测试的人笑了,说我居然0.1+02都不会算。
小帅忍不住笑了:0.1+0.2 =0.3 这你也能算错?
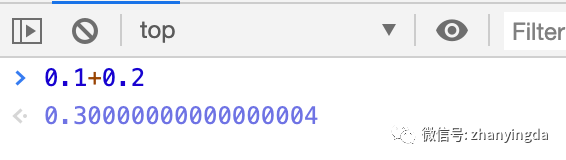
小云不服道:这不能怪我,谁知道计算机那么傻,居然不能精确计算0.1+0.2,不信你看,结果居然是0.30000000000000004,0.3后面还有一长串00000。
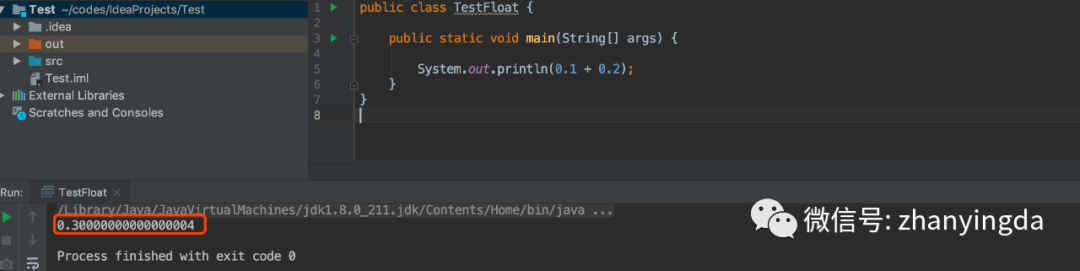
小帅会心一笑:老师上课讲浮点数的时候,你是不是翘课打游戏去了啊。
小云不好意思的说:当时上课的时候,不小心笔掉地上了,我弯腰捡了起来,漏听了几句话,后面就再也听不懂了。。。
小帅:。。。
那我就重新给你讲讲,计算机是二进制的世界,所有的数据都是二进制表示的,例如:十进制的5用二进制表示就是101,
计算过程如下:
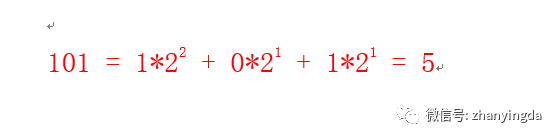
小云:那十进制的小数是怎么表示的呢?
小帅:这个问题问的有深度,是如下形式
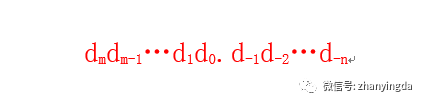
其中d的取值范围是0~9,小数点左边的数代表整数,小数点右边的数代表小数。例如十进制的23.45表示如下:

类似的二进制的数取值范围是0~1,小数点左边的数代表整数,小数点右边的数代表小数。例如二进制的101.11转换成十进制如下:
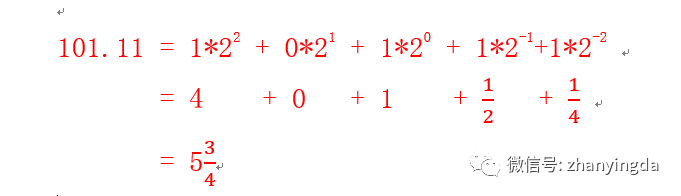
现在我们试着用二进制表示0.3看看,先找个比较接近的数二进制0.01
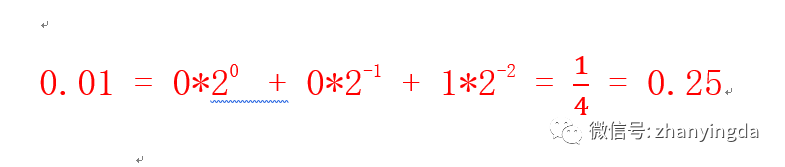
0.25太小了
那我们多加一位二进制数试试,
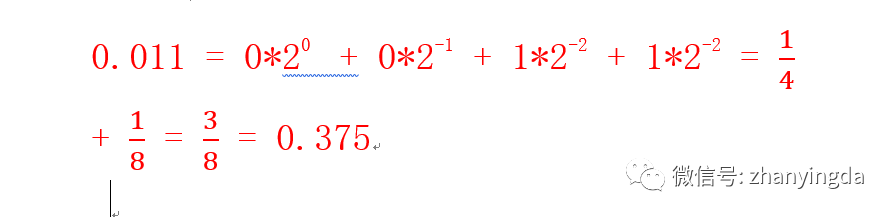
0.375太大了
这次缩小点试试
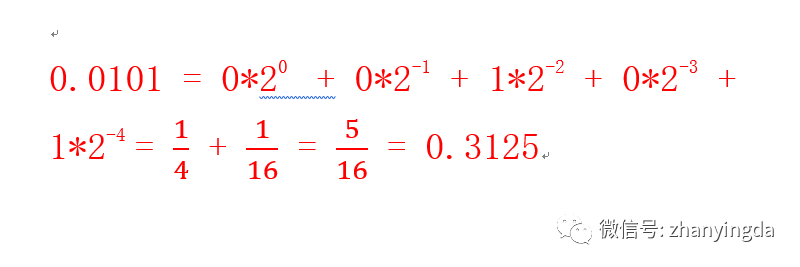
0.3125还是太大
我去,我继续试试试

事实证明,二进制数无法精确表示0.3,就像十进制无法精确表示1/3一样:

所以二进制表示0.3只能用近似值,再转换成十进制就表示成 0.30000000000000004 了
小云豁然开朗:那计算机里小数点的浮点计算怎么处理呢?
小帅在电脑前面啪啪啪的敲了一会代码,显示出了程序员应有的成熟与稳重,指着屏幕说:
java可以用 BigDecimal 类来进行浮点数计算

(BigDecimal没有减法运算方法,减法就是加上一个负数)计算结果如下:

python 中也有Decimal类
直接计算同样有问题
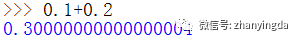
用Decimal计算正确

JavaScript 没有Decimal,直接计算也同样有问题
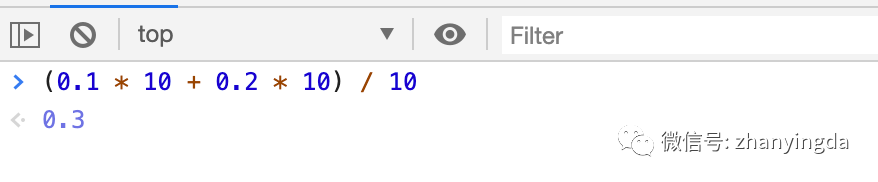
js中浮点数计算要先转换成整数,然后在计算,最后转换回小数
最后,涉及到浮点数计算,要特别小心,如果是不需要很精确的计算直接运算就行,如果系统涉及到金额计算,一定要用Decimal类或者放大成整数后计算,还有比较常见的一种做法是,以分为单位,比如100表示1元,10表示1角,1表示1分,这样就避免了计算小数,整数计算是没有这种精度问题的,这也算一种小技巧。
小云崇拜得看着小帅从电脑桌前站起来,小帅脸上露出了纯洁的微笑,一本《深入理解计算机系统》的书不小心从电脑桌上滑落,小云刚好瞄到第二章二进制小数的介绍。。。