12 Julia科学计算

发布于

科学计算

科学计算必备DataFrames

DataFrames基本操作

跟Python中的pandas的用法很像，相信用过Pandas的朋友上手应该无压力

DataFrame定义

新建一个DataFrame并增加4列内容

代码语言：javascript
复制
using DataFrames
df1 = DataFrame()
df1[:clo1] = Array([1.0,2.0,3.0])
df1[:clo2] = Array([4.0,5.0,6.0])
df1[:clo3] = Array([7.0,8.0,9.0])
df1[:ID] = Array(['a','b','c'])
show(df1)
>>3×4 DataFrame
│ Row │ clo1    │ clo2    │ clo3    │ ID   │
│     │ Float64 │ Float64 │ Float64 │ Char │
├─────┼─────────┼─────────┼─────────┼──────┤
│ 1   │ 1.0     │ 4.0     │ 7.0     │ 'a'  │
│ 2   │ 2.0     │ 5.0     │ 8.0     │ 'b'  │
│ 3   │ 3.0     │ 6.0     │ 9.0     │ 'c'  │

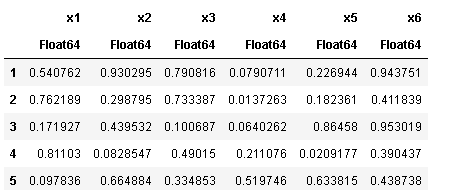
如果没有指定列名，则默认是x1,x2...

代码语言：javascript
复制
df2 = DataFrame(rand(5,6))

image

在DataFrame定义时直接指定内容

代码语言：javascript
复制
df3 = DataFrame([collect(1:3),collect(4:6)], [:A, :B])
>>    A   B
  Int64    Int64
1    1   4
2    2   5
3    3   6

DataFrame合并

代码语言：javascript
复制
df2 = DataFrame()
df2[:clo1] = Array([11.0,12.0,13.0])
df2[:clo2] = Array([14.0,15.0,16.0])
df2[:clo3] = Array([17.0,18.0,19.0])
df2[:ID] = Array(['a','b','c'])
show(df2)
>>3×4 DataFrame
│ Row │ clo1    │ clo2    │ clo3    │ ID   │
│     │ Float64 │ Float64 │ Float64 │ Char │
├─────┼─────────┼─────────┼─────────┼──────┤
│ 1   │ 11.0    │ 14.0    │ 17.0    │ 'a'  │
│ 2   │ 12.0    │ 15.0    │ 18.0    │ 'b'  │
│ 3   │ 13.0    │ 16.0    │ 19.0    │ 'c'  │

合并df1和df2

代码语言：javascript
复制
df3 = join(df1, df2, on=:ID)

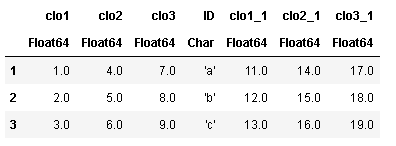
列重命名

代码语言：javascript
复制
rename!(df1, :clo1, :cool1)

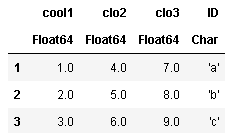
索引

代码语言：javascript
复制
df = DataFrame(rand(5,6))
show(df)

5×6 DataFrame

│ Row │ x1        │ x2       │ x3       │ x4       │ x5       │ x6        │

│     │ Float64   │ Float64  │ Float64  │ Float64  │ Float64  │ Float64   │

├─────┼───────────┼──────────┼──────────┼──────────┼──────────┼───────────┤

│ 1   │ 0.678851  │ 0.514764 │ 0.829835 │ 0.996105 │ 0.427939 │ 0.163515  │

│ 2   │ 0.366487  │ 0.834486 │ 0.588859 │ 0.398066 │ 0.45738  │ 0.577453  │

│ 3   │ 0.0945619 │ 0.231903 │ 0.715664 │ 0.538696 │ 0.813534 │ 0.100683  │

│ 4   │ 0.102987  │ 0.269429 │ 0.292984 │ 0.719276 │ 0.756749 │ 0.705312  │

│ 5   │ 0.328692  │ 0.420872 │ 0.545552 │ 0.793303 │ 0.670403 │ 0.0619233 │

用索引取值，取24列

代码语言：javascript
复制
df[2:4]

>>       x2          x3          x4

Float64        Float64     Float64

1    0.514764    0.829835    0.996105

2    0.834486    0.588859    0.398066

3    0.231903    0.715664    0.538696

4    0.269429    0.292984    0.719276

5    0.420872    0.545552    0.793303

用名称取值

代码语言：javascript
复制
df.x1

>>5-element Array{Float64,1}:

0.6788506862994854

0.366486647281848

0.09456191069734388

0.10298681965872736

0.32869200293154477

取24行，x1,x3列

代码语言：javascript
复制
df[2:4, [:x1, :x3]]

>>      x1          x3

Float64      Float64

1    0.366487    0.588859

2    0.0945619   0.715664

3    0.102987    0.292984

for循环遍历

代码语言：javascript
复制
for row in eachrow(df)

println(row)

end

查看df的描述信息

代码语言：javascript
复制
describe(df)

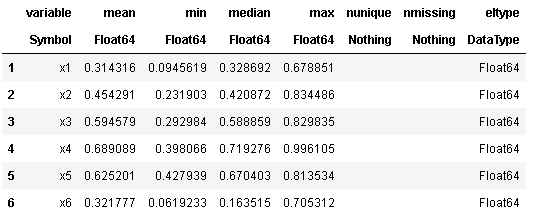
排序

代码语言：javascript
复制
sort!(df, cols = [:x1])

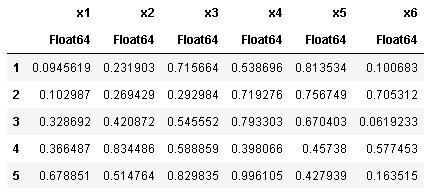
DataFrame的csv文件操作

代码语言：javascript
复制
using CSV

df = DataFrame(rand(5,6))

show(df)

>>5×6 DataFrame

│ Row │ x1       │ x2       │ x3        │ x4       │ x5        │ x6        │

│     │ Float64  │ Float64  │ Float64   │ Float64  │ Float64   │ Float64   │

├─────┼──────────┼──────────┼───────────┼──────────┼───────────┼───────────┤

│ 1   │ 0.173904 │ 0.981004 │ 0.997001  │ 0.742527 │ 0.816245  │ 0.950086  │

│ 2   │ 0.946748 │ 0.661713 │ 0.0734147 │ 0.181932 │ 0.175604  │ 0.0550761 │

│ 3   │ 0.638618 │ 0.30026  │ 0.926336  │ 0.427942 │ 0.803738  │ 0.481783  │

│ 4   │ 0.156693 │ 0.943436 │ 0.0614211 │ 0.35279  │ 0.0692527 │ 0.417888  │

│ 5   │ 0.351843 │ 0.64204  │ 0.934611  │ 0.910804 │ 0.715309  │ 0.3677    │

写文件

代码语言：javascript
复制
CSV.write("df123.csv",df)

读文件

代码语言：javascript
复制
data = CSV.read("df123.csv")

DataFrame中的宏

@where

代码语言：javascript
复制
using DataFramesMeta

@where(df, :x1 .> 0.2)

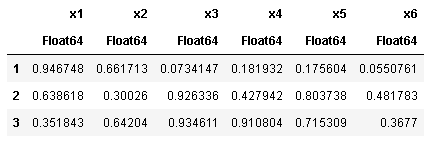
image

@with

代码语言：javascript
复制
@with(df, :x2 .+ 1)

>>5-element Array{Float64,1}:

1.9810036040861598

1.6617132284630372

1.3002596213068984

1.9434355174941438

1.6420398463078156

@select

代码语言：javascript
复制
@select(df, :x3)

>>   x3

Float64

1    0.997001

2    0.0734147

3    0.926336

4    0.0614211

5    0.934611
代码语言：javascript
复制
@select(df, p = 2 * :x1, :x2)

>>     p         x2

Float64        Float64

1    0.347808    0.981004

2    1.8935      0.661713

3    1.27724     0.30026

4    0.313385    0.943436

5    0.703686    0.64204

RDatasets

RDatasets是Julia中的一个数据集，里面包含了很多可以学习和验证的数据，其中就包括iris数据集。

iris数据集介绍

在机器学习领域，有大量的公开数据集。iris就是其中非常重要的一个。

Iris Data Set（鸢尾属植物数据集）是一个历史很悠久的数据集，它首次出现在著名的英国统计学家和生物学家Ronald Fisher 1936年的论文《The use of multiple measurements in taxonomic problems》中，被用来介绍线性判别式分析。在这个数据集中，包括了三类不同的鸢尾属植物：Iris Setosa，Iris Versicolour，Iris Virginica。每类收集了50个样本，因此这个数据集一共包含了150个样本。

该数据集测量了所有150个样本的4个特征，分别是：

  • sepal length（花萼长度）
  • sepal width（花萼宽度）
  • petal length（花瓣长度）
  • petal width（花瓣宽度）

以上四个特征的单位都是厘米（cm）。

通常使用m表示样本量的大小，n表示每个样本所具有的特征数。

代码语言：javascript
复制
using RDatasets
代码语言：javascript
复制
iris = dataset("datasets", "iris")
代码语言：javascript
复制
features = convert(Array, iris[:, 1:4])

labels = convert(Array, iris[:, 5])

Gadfly绘图

代码语言：javascript
复制
p = plot(iris, x=:SepalLength, y=:SepalWidth, Geom.point)

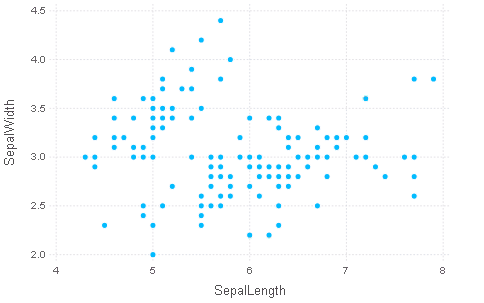
把图片输出到文件

代码语言：javascript
复制
img = SVG("iris_plot.SVG", 10cm, 8cm)

draw(img, p)

用线连接起来

代码语言：javascript
复制
p = plot(iris, x=:SepalLength, y=:SepalWidth, Geom.point, Geom.line)

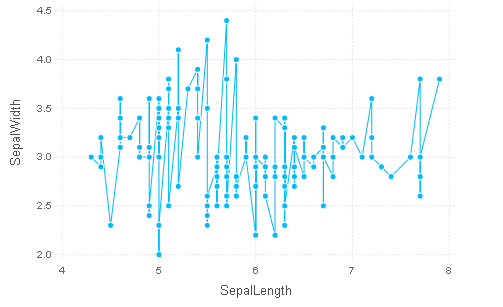
以Species作为颜色依据

代码语言：javascript
复制
p = plot(iris, x=:SepalLength, y=:SepalWidth, Geom.point, color=:Species)

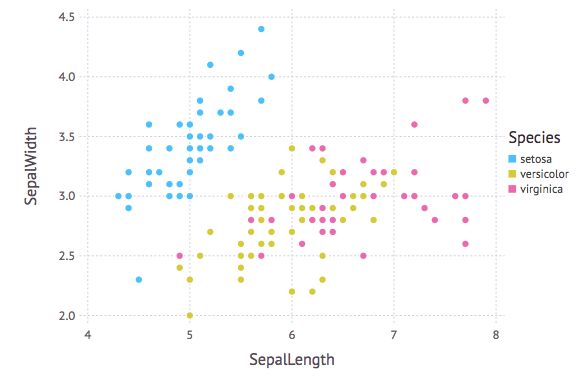
在图中加上lable

代码语言：javascript
复制
p = plot(iris, x=:SepalLength, y=:SepalWidth, label=:Species,  color=:Species, Geom.point, Geom.label)

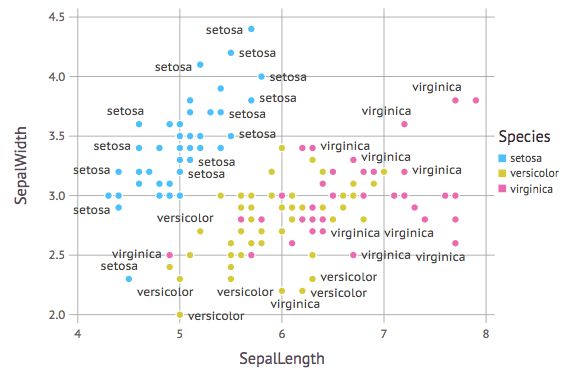
柱状图

代码语言：javascript
复制
fig1a = plot(iris, x="SepalLength", y="SepalWidth", Geom.point)

fig1b = plot(iris, x="SepalWidth", Geom.bar)

fig1 = hstack(fig1a, fig1b)

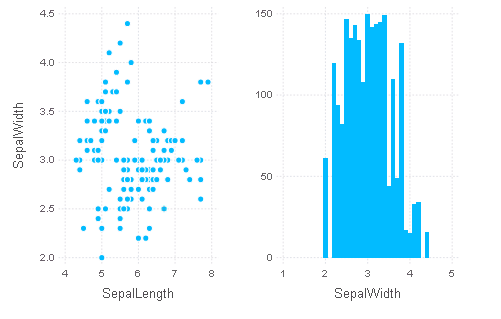
概率分布

代码语言：javascript
复制
using Distributions

生成均值20，标准差2.0的正态分布模型

代码语言：javascript
复制
n1 = Normal(20,2.0)


params(n1)

>>(20,2.0)


fieldnames(typeof(n1))

>>(:μ, :σ)

Normal的类型是UnionAll

代码语言：javascript
复制
typeof(Normal)

>>UnionAll

生成满足n1模型的随机数

代码语言：javascript
复制
rand(n1,100)

二项分布

代码语言：javascript
复制
b = Binomial(20, 0.8)

rand(b, 1000)

概率密度

代码语言：javascript
复制
n = Normal()

pdf(n, 0.4)

>>0.36827014030332333


pdf(n, 0)      #标准正态分布在x=0处的概率密度为0.3989...

>>0.3989422804014327

分布函数

代码语言：javascript
复制
cdf(n, 0.4)

>>0.6554217416103242

分位数

代码语言：javascript
复制
quantile.(n, [0.25, 0.5, 0.95])

>>3-element Array{Float64,1}:

-0.6744897501960818

0.0

1.6448536269514717

对于随机数rand(10),按Normal分布分析它的参数值

代码语言：javascript
复制
fit(Normal, rand(10))

>>Normal{Float64}(μ=0.41375573240875224, σ=0.25565343114046984)

StatsBase库:里面也包含了统计学的常用函数

代码语言：javascript
复制
using StatsBase
代码语言：javascript
复制
a = collect(1:6)

b = collect(4:9)

countne(a,b) #按顺序对比  1!=4  2!=5 ... 6!=9

>>6
代码语言：javascript
复制
a = [1,2,3,4,5]

b = [4,1,3,2,5]

counteq(a,b) # 按顺序对比 两个向量中相等元素的个数

>>2
代码语言：javascript
复制
L1dist(a,b) # abs(a[1]-b[1]) + ... + abs(a[n]-b[n])

>>6.0


L2dist(a, b)  # sqrt((a[1] - b[1])^2 + ... + (a[n] - b[n])^2)


meanad(a, b) # mean absolute deviation L1dist(a,b)/n

>>1.2
代码语言：javascript
复制
sample(a)  # 从a中采样一次数据
代码语言：javascript
复制
sample(a, 3) # 从a中采样3次数据，返回1维Array

>>3-element Array{Int64,1}:

3

2

3
代码语言：javascript
复制
a1 = [1, 10, 20, 30]

a2 = [100, 200, 300]

sample!(a1, a2) # 从a1中，按照a2的类型取出length(a2)次数据

>>3-element Array{Int64,1}:

20

10

30
代码语言：javascript
复制
a1 = [1, 10, 20, 30]

a2 = [100.0, 200.0, 300.0]

sample!(a1, a2)

>>3-element Array{Float64,1}:

1.0

30.0

1.0

其他常用函数

代码语言：javascript
复制
x = [1.0, 2.0, 3.0, 4.0]

autocov(x)

autocov(x, [2,3])

autocor(x)

autocor(x, [2,3])

y = [3. , 4., 5., 6.]

crosscov(x, y)

crosscov(x, y, [2,3])

时间序列

代码语言：javascript
复制
using TimeSeries

新建Date变量

代码语言：javascript
复制
dates = collect(Date(2018, 1,1) :Day(1): Date(2018, 12, 31))

dates[1:20]

新建TimeArray

代码语言：javascript
复制
ta = TimeArray(dates, rand(length(dates),2))

>>365×2 TimeArray{Float64,2,Date,Array{Float64,2}} 2018-01-01 to 2018-12-31

│            │ A      │ B      │

├────────────┼────────┼────────┤

│ 2018-01-01 │ 0.7933 │ 0.4359 │

│ 2018-01-02 │ 0.6347 │ 0.7234 │

│ 2018-01-03 │ 0.2454 │ 0.6826 │

│ 2018-01-04 │ 0.767  │ 0.9007 │

│ 2018-01-05 │ 0.1884 │ 0.5429 │

│ 2018-01-06 │ 0.7809 │ 0.2292 │

│ 2018-01-07 │ 0.9329 │ 0.0098 │

│ 2018-01-08 │ 0.0032 │ 0.7566 │

│ 2018-01-09 │ 0.1355 │ 0.8986 │

│ 2018-01-10 │ 0.9274 │ 0.6022 │

│ 2018-01-11 │ 0.6483 │ 0.53   │

│ 2018-01-12 │ 0.8594 │ 0.0237 │

⋮

│ 2018-12-21 │ 0.7245 │ 0.5286 │

│ 2018-12-22 │ 0.9374 │ 0.8508 │

│ 2018-12-23 │ 0.0528 │ 0.1361 │

│ 2018-12-24 │ 0.1184 │ 0.6156 │

│ 2018-12-25 │ 0.3645 │ 0.7896 │

│ 2018-12-26 │ 0.023  │ 0.8259 │

│ 2018-12-27 │ 0.0942 │ 0.9326 │

│ 2018-12-28 │ 0.6124 │ 0.3102 │

│ 2018-12-29 │ 0.5602 │ 0.3305 │

│ 2018-12-30 │ 0.273  │ 0.7611 │

│ 2018-12-31 │ 0.7595 │ 0.1093 │

取出时间戳

代码语言：javascript
复制
timestamp(ta::TimeArray)

取值

代码语言：javascript
复制
values(ta::TimeArray)

取列名

代码语言：javascript
复制
colnames(ta::TimeArray)

机器学习

MLBase

代码语言：javascript
复制
using MLBase

机器学习基础库，不包含任何机器学习的算法，但为机器学习提供很多的必要工具，比如Cross validation等

先来看下MLBase中几个做简单数据处理的函数

代码语言：javascript
复制
repeach(1:3, 2)

>>6-element Array{Int64,1}:

1

1

2

2

3

3


repeach(["a", "b", "c"], 2)

>>6-element Array{String,1}:

"a"

"a"

"b"

"b"

"c"

"c"


repeach(["a", "b", "c"], [1, 2, 3])

>>6-element Array{String,1}:

"a"

"b"

"b"

"c"

"c"

"c"
代码语言：javascript
复制
A = reshape(collect(1:6), 2, 3)

repeachcol(A, 2)

>>2×6 Array{Int64,2}:

1  1  3  3  5  5

2  2  4  4  6  6
代码语言：javascript
复制
repeachrow(A, 2)

>>4×3 Array{Int64,2}:

1  3  5

1  3  5

2  4  6

2  4  6
代码语言：javascript
复制
labels = labelmap(['a', 'b', 'b', 'c', 'c', 'c'])

>>LabelMap (with 3 labels):

[1] a

[2] b

[3] c
代码语言：javascript
复制
labelencode(labels, ['b', 'c', 'c', 'a'])

>>4-element Array{Int64,1}:

2

3

3

1

决策树

使用iris数据集

代码语言：javascript
复制
using RDatasets

iris = dataset("datasets", "iris")

features = convert(Array, iris[:, 1:4])

labels = convert(Array, iris[:, 5])

调用决策树

代码语言：javascript
复制
using DecisionTree

在该库中，包含了

  • Decision Tree Classifier
  • Random Forest Classifier
  • Adaptive-Boosted Decision Stumps Classifier
  • Regression Tree
  • Regression Random Forest

我们这里只介绍分类模型，即前三种算法模型

代码语言：javascript
复制
model = build_tree(labels, features)

>>Decision Tree

Leaves: 9

Depth:  5
代码语言：javascript
复制
model = prune_tree(model, 0.9)

>>Decision Tree

Leaves: 8

Depth:  5
代码语言：javascript
复制
print_tree(model, 5)

>>Feature 3, Threshold 2.45

L-> setosa : 50/50

R-> Feature 4, Threshold 1.75

L-> Feature 3, Threshold 4.95

L-> versicolor : 47/48

R-> Feature 4, Threshold 1.55

L-> virginica : 3/3

R-> Feature 3, Threshold 5.449999999999999

L-> versicolor : 2/2

R-> virginica : 1/1

R-> Feature 3, Threshold 4.85

L-> Feature 2, Threshold 3.1

L-> virginica : 2/2

R-> versicolor : 1/1

R-> virginica : 43/43
代码语言：javascript
复制
print_tree(model, 3)

>>Feature 3, Threshold 2.45

L-> setosa : 50/50

R-> Feature 4, Threshold 1.75

L-> Feature 3, Threshold 4.95

L-> versicolor : 47/48

R->

R-> Feature 3, Threshold 4.85

L->

R-> virginica : 43/43

按照下面的方式

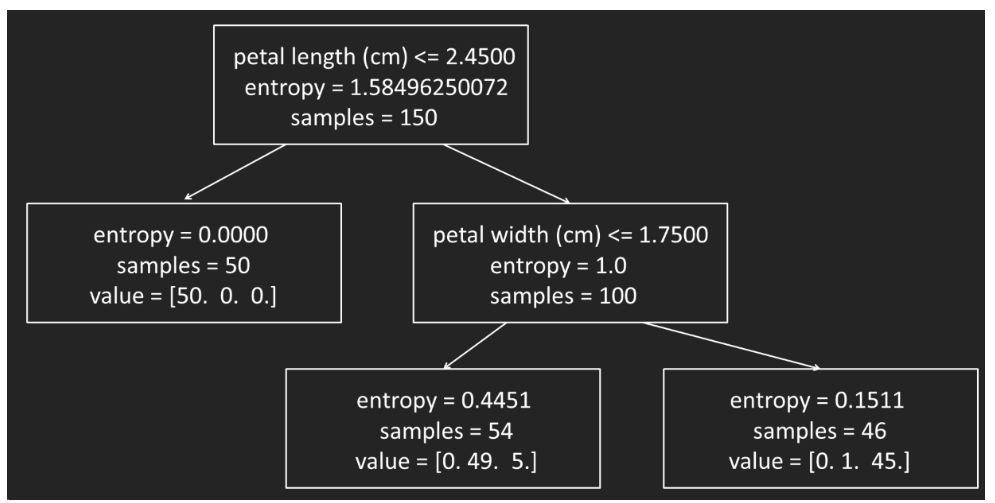
用决策树模型做判断

代码语言：javascript
复制
apply_tree(model, [5.9, 3.0, 5.1, 1.9])

>>"virginica"

apply_tree(model, [1.9, 2.0, 2.1, 1.9])

>>"setosa"

nfold cross validation for pruned tree

代码语言：javascript
复制
n_folds=3

accuracy = nfoldCV_tree(labels, features, n_folds, 0.9)

>>3×3 Array{Int64,2}:

24   0   0

0  13   0

0   0  13

3×3 Array{Int64,2}:

12   0   0

0  17   0

0   0  21

3×3 Array{Int64,2}:

14   0   0

0  20   0

0   1  15


Fold 1

Classes:  ["setosa", "versicolor", "virginica"]

Matrix:

Accuracy: 1.0

Kappa:    1.0


Fold 2

Classes:  ["setosa", "versicolor", "virginica"]

Matrix:

Accuracy: 1.0

Kappa:    1.0


Fold 3

Classes:  ["setosa", "versicolor", "virginica"]

Matrix:

Accuracy: 0.98

Kappa:    0.9695863746958637


Mean Accuracy: 0.9933333333333333

3-element Array{Float64,1}:

1.0

1.0

0.98

adaptive boosting

构造adaboost_stumps模型

代码语言：javascript
复制
model, coeffs = build_adaboost_stumps(labels, features, 10)

>>(Ensemble of Decision Trees

Trees:      10

Avg Leaves: 2.0

Avg Depth:  1.0, [0.346574, 0.255413, 0.264577, 0.335749, 0.288846, 0.258287, 0.356882, 0.298766, 0.242485, 0.349976])

应用模型判断

代码语言：javascript
复制
apply_adaboost_stumps(model, coeffs, [5.9, 3.0, 5.1, 1.9])

>>"virginica"

adaboost nfold cross-validation

代码语言：javascript
复制
# 3 folds, 8 iteration

accuracy = nfoldCV_stumps(labels, features, 3, 8)

随机森林

构造随机森林模型

代码语言：javascript
复制
# 2 random features, 10 trees, 0.5 portion of samples

model = build_forest(labels, features, 2, 10, 0.5)

>>Ensemble of Decision Trees

Trees:      10

Avg Leaves: 6.4

Avg Depth:  4.4

应用模型判断

代码语言：javascript
复制
apply_forest(model, [5.9, 3.0, 5.1, 1.9])

>>"virginica"

forest nfold cross-validation

代码语言：javascript
复制
accuracy = nfoldCV_forest(labels, features, 3, 2)

>>3×3 Array{Int64,2}:

12   0   0

0  15   0

0   1  22

3×3 Array{Int64,2}:

18   0   0

0  13   2

0   1  16

3×3 Array{Int64,2}:

20   0   0

0  20   0

0   0  10


Fold 1

Classes:  ["setosa", "versicolor", "virginica"]

Matrix:

Accuracy: 0.98

Kappa:    0.9689440993788819


Fold 2

Classes:  ["setosa", "versicolor", "virginica"]

Matrix:

Accuracy: 0.94

Kappa:    0.9096385542168673


Fold 3

Classes:  ["setosa", "versicolor", "virginica"]

Matrix:

Accuracy: 1.0

Kappa:    1.0


Mean Accuracy: 0.9733333333333333

3-element Array{Float64,1}:

0.98

0.94

1.0

MultivariateStats

PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

代码语言：javascript
复制
using MultivariateStats, RDatasets


load iris dataset


iris = dataset("datasets", "iris")


split half to training set


Xtr = convert(Array,(iris[1:2:end,1:4]))'

Xtr_labels = convert(Array,(iris[1:2:end,5]))


split other half to testing set


Xte = convert(Array,(iris[2:2:end,1:4]))'

Xte_labels = convert(Array,(iris[2:2:end,5]))


suppose Xtr and Xte are training and testing data matrix,


with each observation in a column


train a PCA model, allowing up to 3 dimensions


M = fit(PCA, Xtr; maxoutdim=3)


apply PCA model to testing set


Yte = transform(M, Xte)


reconstruct testing observations (approximately)


Xr = reconstruct(M, Yte)


group results by testing set labels for color coding


setosa = Yte[:,Xte_labels.=="setosa"]

versicolor = Yte[:,Xte_labels.=="versicolor"]

virginica = Yte[:,Xte_labels.=="virginica"]
代码语言：javascript
复制
size(Xte)

>>(4, 75)

size(Yte)

>>(3, 75)

把降维后的数据画出来

代码语言：javascript
复制
using Plots

p = scatter(setosa[1,:],setosa[2,:],setosa[3,:],marker=:circle,linewidth=0)
代码语言：javascript
复制
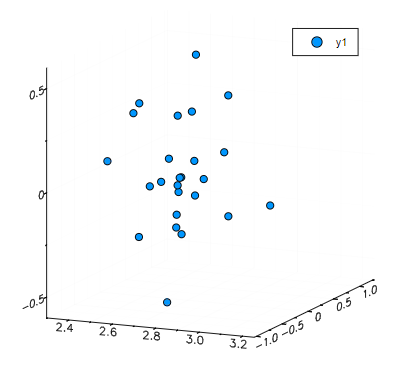
scatter!(versicolor[1,:],versicolor[2,:],versicolor[3,:],marker=:circle,linewidth=0)
代码语言：javascript
复制
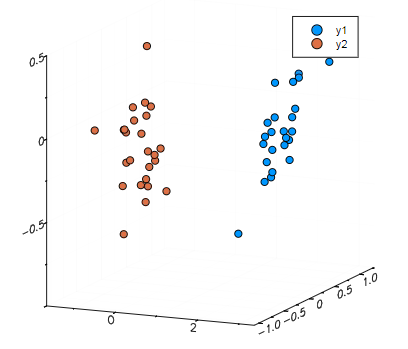
scatter!(virginica[1,:],virginica[2,:],virginica[3,:],marker=:circle,linewidth=0)

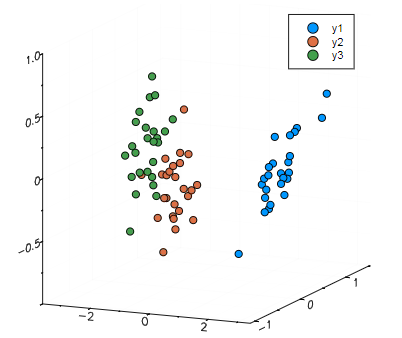
SVM

代码语言：javascript
复制
using LIBSVM
代码语言：javascript
复制
using RDatasets

iris = dataset("datasets", "iris")

features = convert(Array, iris[:, 1:4])

labels = convert(Array, iris[:, 5])

features_train, features_test = features[1:2:end, :], features[2:2:end, :]

labels_train, lables_test = labels[1:2:end], labels[2:2:end]
代码语言：javascript
复制
model = svmtrain(features_train', labels_train)
代码语言：javascript
复制
(predicted_labels, decision_values) = svmpredict(model, features_test')

检查预测结果

代码语言：javascript
复制
using Statistics

mean(predicted_labels .== lables_test) * 1.0

predicted_labels .== lables_test

>>75-element BitArray{1}:

true

true

true

true

true

true

true

true

true

true

true

true

true

⋮

true

true

true

true

true

true

true

true

true

true

true

true

线性回归

代码语言：javascript
复制
using GLM, GLMNet, DataFrames

lm模型

代码语言：javascript
复制
data = DataFrame(X=[1,2,3], Y=[2,4,7])

ols = lm(@formula(Y ~ X), data)

>>StatsModels.DataFrameRegressionModel{LinearModel{LmResp{Array{Float64,1}},DensePredChol{Float64,LinearAlgebra.Cholesky{Float64,Array{Float64,2}}}},Array{Float64,2}}


Formula: Y ~ 1 + X


Coefficients:

Estimate Std.Error  t value Pr(>|t|)

(Intercept)  -0.666667   0.62361 -1.06904   0.4788

X                  2.5  0.288675  8.66025   0.0732

线性回归模型标准差

代码语言：javascript
复制
stderror(ols)

>>2-element Array{Float64,1}:

0.6236095644623245

0.2886751345948133

应用模型

代码语言：javascript
复制
newX = DataFrame(X=[2,3,4]);

GLM.predict(ols, newX)

>>3-element Array{Union{Missing, Float64},1}:

4.333333333333332

6.833333333333335

9.33333333333334
代码语言：javascript
复制
data = DataFrame(X=[1,2,3], Y=[2,4,6])

ols = lm(@formula(Y ~ X), data)

newX = DataFrame(X=[2,3,4])

GLM.predict(ols, newX)

>>3-element Array{Union{Missing, Float64},1}:

4.0

6.0

8.0

glm模型

代码语言：javascript
复制
data = DataFrame(X=[0,1,2,3,4], Y=[0.1296,0.0864,0.0576,0.0384,0.0256])

probit = glm(@formula(Y ~ X), data, Binomial(), ProbitLink())

>>StatsModels.DataFrameRegressionModel{GeneralizedLinearModel{GlmResp{Array{Float64,1},Binomial{Float64},ProbitLink},DensePredChol{Float64,LinearAlgebra.Cholesky{Float64,Array{Float64,2}}}},Array{Float64,2}}


Formula: Y ~ 1 + X


Coefficients:

Estimate Std.Error   z value Pr(>|z|)

(Intercept)   -1.14184   1.32732 -0.860259   0.3896

X            -0.208282  0.659347 -0.315891   0.7521
代码语言：javascript
复制
newX = DataFrame(X=[1,2,3,4])

GLM.predict(probit, newX)

>>4-element Array{Union{Missing, Float64},1}:

0.08848879660655808

0.05956904945792997

0.03864063839150974

0.024136051585243873

线性回归模型处理iris数据集

代码语言：javascript
复制
data = DataFrame();

data[:x] = iris[1:50, :SepalWidth]

data[:y] = iris[1:50, :SepalLength]
代码语言：javascript
复制
model = lm(@formula(y ~ x), data)

>>StatsModels.DataFrameRegressionModel{LinearModel{LmResp{Array{Float64,1}},DensePredChol{Float64,LinearAlgebra.Cholesky{Float64,Array{Float64,2}}}},Array{Float64,2}}


Formula: y ~ 1 + x


Coefficients:

Estimate Std.Error t value Pr(>|t|)

(Intercept)     2.639  0.310014 8.51251   <1e-10

x             0.69049 0.0898989 7.68074    <1e-9

把LM拟合后的曲线跟原始的曲线做对比

代码语言：javascript
复制
using Plots

plot(GLM.predict(model))

plot!(data[:y])

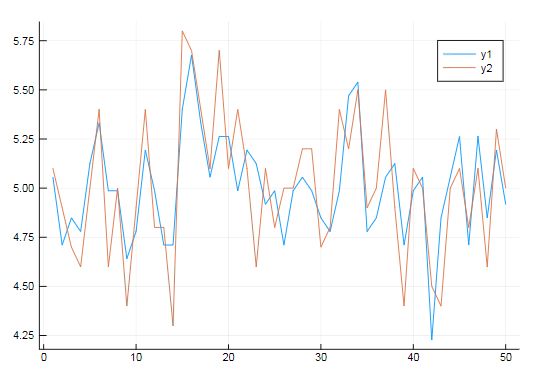
用GLM处理iris数据集

代码语言：javascript
复制
model = glm(@formula(y~x), data, Normal(), IdentityLink())

>>StatsModels.DataFrameRegressionModel{GeneralizedLinearModel{GlmResp{Array{Float64,1},Normal{Float64},IdentityLink},DensePredChol{Float64,LinearAlgebra.Cholesky{Float64,Array{Float64,2}}}},Array{Float64,2}}


Formula: y ~ 1 + x


Coefficients:

Estimate Std.Error z value Pr(>|z|)

(Intercept)     2.639  0.310014 8.51251   <1e-16

x             0.69049 0.0898989 7.68074   <1e-13

把GLM拟合后的曲线跟原始的曲线做对比

代码语言：javascript
复制
using Plots

plot(GLM.predict(model))

plot!(data[:y])
代码语言：javascript
复制
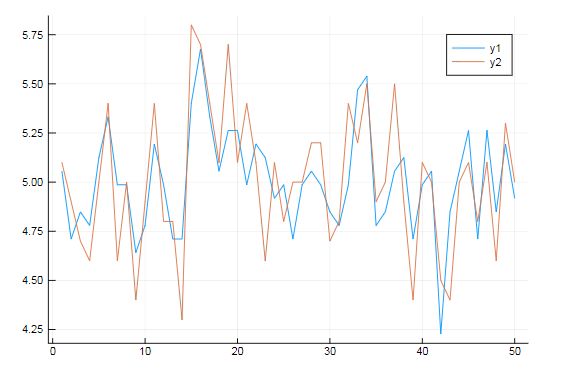
# Estimates for coefficents

coef(model)


Standard errors of coefficents


stderror(model)


Covariance of coefficents


vcov(model)


RSS


deviance(model)

K-means

代码语言：javascript
复制
using Clustering

using RDatasets

iris = dataset("datasets", "iris")

features = convert(Array, iris[:, 1:4])

labels = convert(Array, iris[:, 5]);
代码语言：javascript
复制
# choose 3 random starting points

initseeds(:rand, convert(Matrix,features'), 3)

>>3-element Array{Int64,1}:

48

80

114
代码语言：javascript
复制
result = kmeans(features, 3)

>>KmeansResult{Float64}([5.1 2.45 0.2; 4.9 2.2 0.2; … ; 6.2 4.4 2.3; 5.9 4.05 1.8], [1, 2, 2, 3], [3.63798e-12, 166.128, 166.127, 0.0], [1, 2, 1], [1.0, 2.0, 1.0], 332.2550000000019, 2, true)
代码语言：javascript
复制
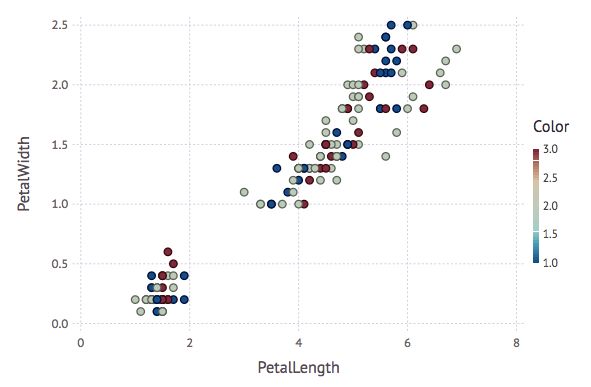
using Gadfly

plot(iris,x="PetalLength",y="PetalWidth",color=result.assignments, Geom.point)

#python#spring#线性回归#机器学习#决策树