数据和信息的区别
数据(data):基本值或事实
信息(information):用有效的方式组织或处理过的数据
数据与计算机

压缩率:压缩后的数据大小除以原始数据大小的值。
无损压缩:不会丢失信息
有损压缩:会丢失信息
模拟数据与离散数据
模拟数据:连续形式表示的信息
数字数据:离散形式表示的信息
数字化:把信息分割成离散的片段
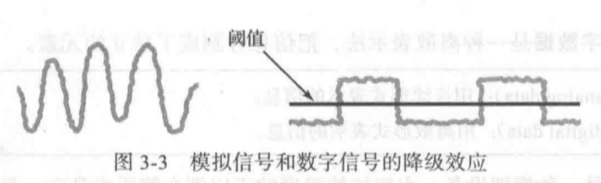
数字信号只在两个极端之间跳跃,被称为脉冲编码机制(PCM)
重新计时: 在信号降级太多之前将它重置为原始状态的行为
定长量数
如果只用定量的数值,那么可以用一半来表示正数,一半来表示负数。符号由数量值决定。
举个例子:

那么不管是执行加法还是减法,都只要把两个数求和然后舍弃进位就可以了。
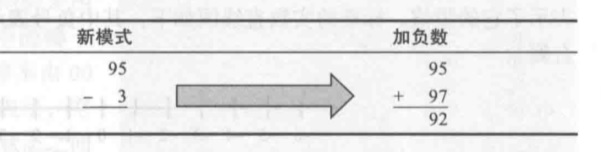
实现十进制补码

二进制补码

把上面的公式中的k改为2,就可以得到二进制的补码公式了。
也就是Negative(I) = 2^(k)-I
利用反码来计算补码
将每一位取反再加一。

溢出
溢出时给结果预留的位数存不下计算出的数值的情况。
溢出是把无限的世界映射到有限的机器上会发生的典型问题。
浮点表示法
符号x尾数x10^exp 的表示法被称为浮点表示法。因为数字的个数是固定的,但是小数点却是浮动的。正指数把小数点向右移动,负指数把小数点向左移动。

要注意的是,在上表的最后一个例子中,丢失了信息,因为我们只能用5位来保存有效数字
相应的,二进制的浮点表示法可以这样定义
符号*尾数*2^exp
把十进制小数转成二进制
之前讲了把十进制整数转换成其他进制的,需要用除法,相反的,把十进制小数转换成其他进制就要用乘法
整个过程直到乘法结果中的小数部分为0为止。

但是对于有的数,比如0.435,转换成二进制,就是个无限小数了。
科学计数法
科学计数法是另一种浮点表示法。由于早期的机器不能输出指数,所以,用字母E来代替‘ ^ ’
比如, 12001.32708 将被写成 1.200132708E+4
文本表示的方法
字符集是字符和他们对应的代码的清单。
ASCII字符集
最初,ASCII字符集用7位表示每个字符,每字节第8位为校验位,用来协助确保数据传输正确。后来,ASCII字符集进化了,用8位表示每个字符。
ASCII的前32个字符没有简单的字符表示法,不能输出到屏幕上,这些字符是为特殊用途保留的,比如回车符和制表符。
Unicode字符集
一般情况下,Unicode字符集的每个字符编码都是16位,但是也可以使用更多的空间来表示每个字符,以便表示额外的字符。
Unicode把ASCII字符集作为了它的子集。Unicode的前256个字符与扩展ASCII字符集中的完全一样。
文本压缩
关键字编码
用特定的单个字符代替高频字符的编码方式
缺陷
1、用来对关键字编码的字符不能出现在原始文本之中
2、某些单词高频出现在特定类型的文本之中,压缩率不稳定
行程长度编码
把重复序列替换为标志字符的编码方式
哈夫曼编码
哈夫曼编码是变长编码,使用不同长度的位串来表示每个字符。
基本思想是用较少的位表示经常出现的字符,把较长的位串留给不经常出现的字符。
哈夫曼编码的解码
由于哈夫曼编码在创建编码的时候,就已经保证了一个字符的位串不会是另一个字符的位串的前缀,因此在从左到右扫描一个位串的时候,当发现一个位串对应一个字符,那么这个位串就一定表示这个字符,不会有歧义。
音频数据表示法
声波是连续的,模拟的,要在计算机上表示声音,那就要把它数字化,分割成离散的、便于管理的片段。
数字化声音的过程叫做采样。
采样率在每秒40000次左右就足够创建合理的声音复制品。采样率低于这个值的时候,人耳听到的声音就会失真。较高采样率生成的声音质量较好,但是达到某种程度后,额外的数据都是无关的,因为人耳分辨不出其中的差别。
激光唱片(CD)存储的是数字化的音频信息
图像与图形表示法
颜色表示法
颜色通常用RGB值来表示,用于表示颜色的数据量称为色深度
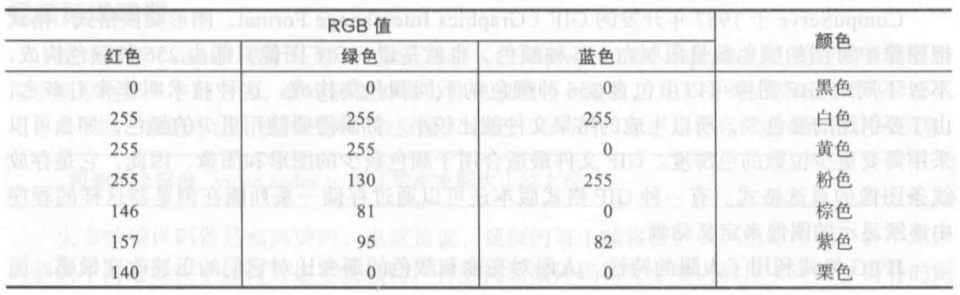
数字化图像与图形
数字化图像是把照片表示成独立的点集,这些点称为像素
分辨率:用于表示图像的像素个数
光栅图形格式:逐个像素存储图像信息的格式
位图文件是最直接的图像表示形式
gif格式的可用颜色数量被限制在256种
JPEG格式利用了人眼的特性,由于人眼对亮度和颜色的渐变比对他们的迅速改变敏感,因此,保存了短距离内色调的平均值。
PNG格式压缩效果比gif更好,同时提供的色深度范围更广,但是不支持动画。
图像的矢量表示法
矢量图是用线段和几何形表示图像的方法。
视频表示法
视频编译码器
编译码器表示压缩器/解压缩器
视频编译码器:用于缩减电影大小的方法
视频编译码器的压缩方式有两种:时间压缩和空间压缩
时间压缩
查找连续帧之间的差别,使用浅矩阵来保存前后两帧的画面的改变部分。
空间压缩
删除一个帧中的冗余信息,空间压缩的基本问题与压缩静态图像是一样的。