计算机模拟定积分的定义

发布于

黎曼(Riemann)对定积分的定义是：积分区间划分为无数子区间，子区间内任意一点的函数值乘以子区间的长度得到一个矩形面积，然后将这些矩形面积累加起来可以得到积分值。

计算π的值

定积分的精确定义

对于定积分

I= \int_0^1 \frac{4}{1+x^2} dx

,在[0,1]内随机取一个数r，通过

\frac{4}{1+r^2} dx

转换成矩形的高。再乘以矩形的宽度1，就是一个矩形的面积。

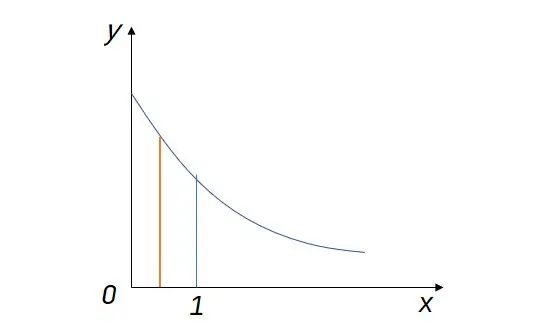
经过多达1000000000次的重复计算，并把这些面积相加，再除以重复计算的次数，得到的值应该是一个接近PI的实数。且计算的次数越多，误差就越小。以下是C++代码

代码语言：javascript
复制

#include <iostream>
#include <iomanip>
#include <random>
#include <cmath>

const size_t n{ 1000000000 };

int main()

{

std::random_device rd;

std::default_random_engine rng{ rd() };


std::uniform_real_distribution&lt; &gt; values{ 0.0, 1.0 };
//生成随机数种子
double sum{};

for (auto counter{ 1 }; counter &lt;= n; ++counter)
{
    sum += (4 / (1 + pow(values(rng), 2)) );

}

std::cout &lt;&lt; &#34;the value of PI is:&#34; &lt;&lt; 
    std::fixed &lt;&lt; std::setprecision(8) &lt;&lt; sum / n &lt;&lt; std::endl;

system(&#34; pause &#34;);
return 0;                                                                                



}

运行结果为

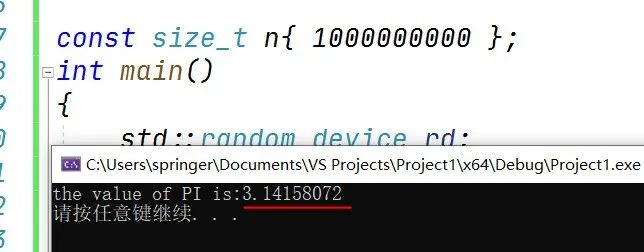
对于uniform_real_distribution是半开范围[ )。也是就是说上面的例子中，能产生0.0，但不会产生1.0。

#c++#distribution