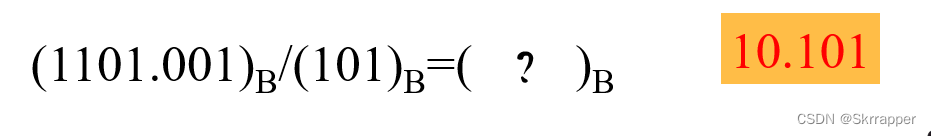我们知道,计算机使用的是二进制来存储信息。而在我们现实生活中,一般是用十进制来表示一系列数值。同时在更加精细的领域还存在着像八进制,十六进制等等一些进制。那么进制究竟是什么?不同的进制之间又是如何实现转换的?接下来我来详细介绍一下。
一、进制是什么?
进制即是进位计数制。是用一组固定的符号和统一的规则来表示数值的方法。生活中常见的进制有十进制、二进制、八进制、十六进制。 在计算机中,数据都是以二进制形式存储的。 进制主要包括三个部分:数位、基数、位权
数位
指数字符号在一个数中所处的位置。
我们平常说的个位数十位数等等,就是数位的概念。
基数
是一种进位计数制允许使用的基本数字符号的个数。
举例r进制,r进制的基数就是r。那么可供使用的计数符号就是r个。由于计数是从0开始记起的,那么r进制的计数符号分别就是0~(r-1)。 我们平常说的逢r进一,也是说记满r就往高位进1.
位权(简称“权”)
是指数制中每个固定位置对应的单位值(常数)。
例如十进制的123,1的位权是100,2的位权是10,3的位权是1。 二进制的110,从右往左,0的位权是2的零次方,第一个1的位权是2的一次方,第二个1的位权是2的二次方。 所以从二进制中可以看出,位权其实是以数字符号所处位置的序号为指数的整数次幂。 在十进制中,位权是10^n 在二进制中,位权是2^n …
二、常见进制介绍以及之间的转换
1.表示
一般情况下,在数字后面用特点的字母(下标)表示该数的进制 二进制;B 十进制:D(可以省略O) 八进制:O 十六进制:H 同时也可以用数字后面加进制来表示。
2.限制
十进制的每位数字的范围:0~9 二进制的每位数字的范围:0~1 八进制的每位数字的范围:0~7 十六进制的每位数字的范围:0~F(f)
3.转换
其他进制数转十进制数
其他进制数按位权展开,然后各项相加。 例如:

十进制数转其他进制数
整数部分:除二取余法 原理:任何一个数除以2得到的余数都是0或1 例如(十转二):

小数部分:乘二取整法 原理:当小数与2相乘时不可能大于1。 例如:

二进制数转八进制数(十六同理)
以小数点为中心,整数部分自右向左每3位一组,最后一组不满3位时补0;小数部分自左向右每3位一组,最后1组不满3位时补0。 举例:
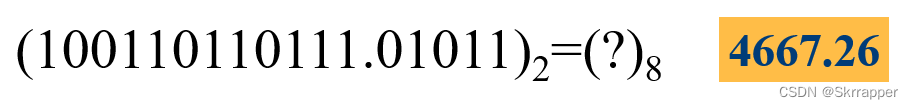
注意这个例子中小数部分最后是不满3位的,所以要补0成为110。
转十六进制数即是将每3位改为每4位。 举例:

同理小数部分不满4位,所以要补0成为1000。
八进制数转二进制数(十六同理)
即:将二转八反过来,将1位八进制数转换为3位二进制数即可。 举例:
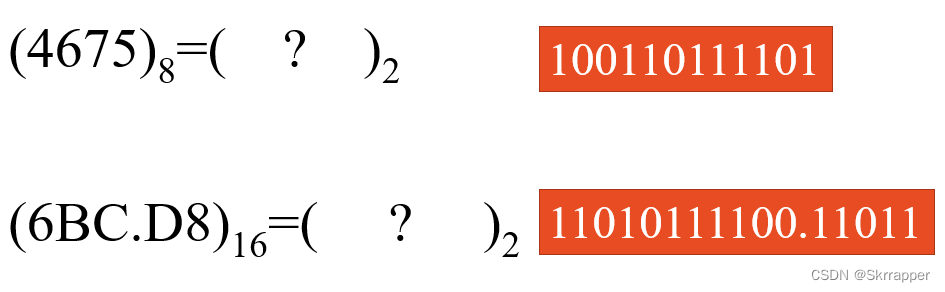
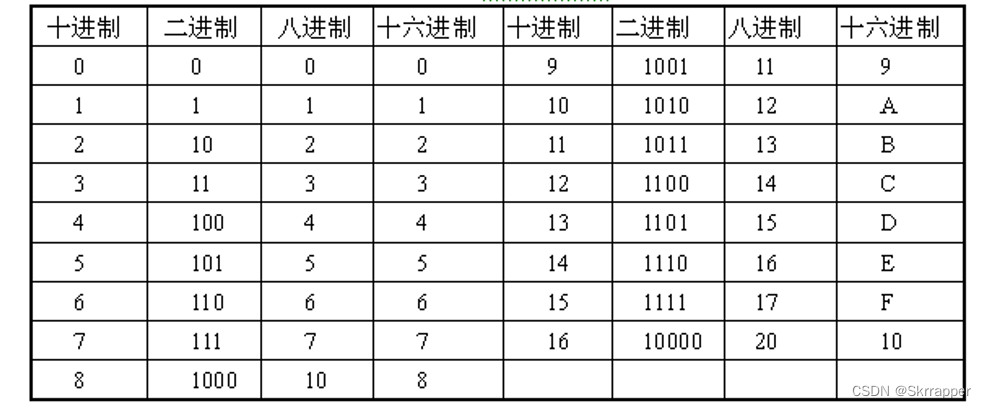
各种进制数码对照表
实际上只要对照表格即可知道对应的关系,就相当于数学中的乘法口诀表一样,熟记于心即可快速转换。
4.基本运算
加法:

举例

减法:

举例:

乘法:

举例:

除法:
举例: