Q3_final.m
% Question 3 | Take Home Exam #3 % Anja Deric | February 24, 2020 clear all; close all; clc;%% Part 1
n=2; experiments = 100;
N = [10 100 1000]; % number of iid samples
num_GMM_picks = zeros(length(N),6);for i = 1:experiments
% True mu and Sigma values for 4-component GMM
mu_true(:,1) = [7;0]; mu_true(:,2) = [6;6];
mu_true(:,3) = [0;0]; mu_true(:,4) = [-1;7];
Sigma_true(:,:,1) = [5 1;1 4]; Sigma_true(:,:,2) = [3 1;1 3];
Sigma_true(:,:,3) = [5 1;1 3]; Sigma_true(:,:,4) = [4 -2;-2 3];
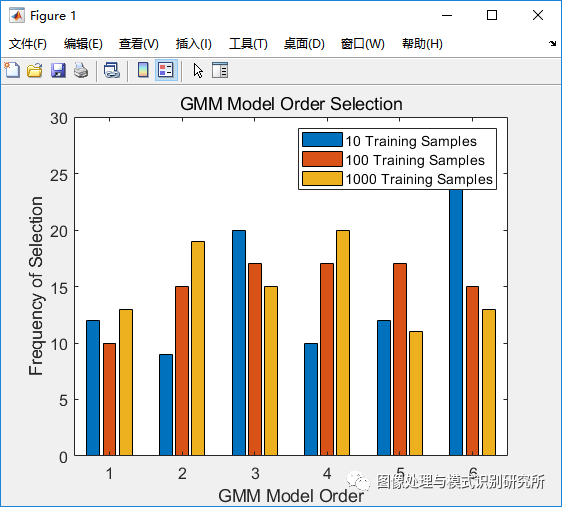
alpha_true = [0.2 0.23 0.27 0.3];% Generate Gaussians with N samples and run cross-validation for i = 1:length(N) x = generate_samples(n, N(i), mu_true, Sigma_true, cumsum(alpha_true)); % Store GMM with highest performance for each iteration GMM_pick = cross_val(x); num_GMM_picks(i,GMM_pick) = num_GMM_picks(i,GMM_pick)+1; end % Plot frequency of model selection bar(num_GMM_picks'); legend('10 Training Samples','100 Training Samples','1000 Training Samples'); title('GMM Model Order Selection'); xlabel('GMM Model Order'); ylabel('Frequency of Selection');end
%% Question 3 Functions
function x = generate_samples(n, N, mu, Sigma, p_cumulative)
% Draws N samples from each class pdf to create GMM
x = zeros(n,N);
for i = 1:N
% Generate random probability
num = rand(1,1);
% Assign point to 1 of 4 Gaussians based on probability
if (num > p_cumulative(1)) == 0
x(:,i) = mvnrnd(mu(:,1),Sigma(:,:,1),1)';
elseif (num > p_cumulative(2)) == 0
x(:,i) = mvnrnd(mu(:,2),Sigma(:,:,2),1)';
elseif (num > p_cumulative(3)) == 0
x(:,i) = mvnrnd(mu(:,3),Sigma(:,:,3),1)';
else
x(:,i) = mvnrnd(mu(:,4),Sigma(:,:,4),1)';
end
end
endfunction best_GMM = cross_val(x)
% Performs EM algorithm to estimate parameters and evaluete performance
% on each data set B times, with 1 through M GMM models consideredB = 10; M = 6; % repetitions per data set; max GMM considered perf_array= zeros(B,M); % save space for performance evaluation % Test each data set 10 times for b = 1:B % Pick random data points to fill training and validation set and % add noise set_size = 500; train_index = randi([1,length(x)],[1,set_size]); train_set = x(:,train_index) + (1e-3)*randn(2,set_size); val_index = randi([1,length(x)],[1,set_size]); val_set = x(:,val_index) + (1e-3)*randn(2,set_size); for m = 1:M % Non-Built-In: run EM algorith to estimate parameters %[alpha,mu,sigma] = EMforGMM(m,train_set,set_size,val_set); % Built-In function: run EM algorithm to estimate parameters GMModel = fitgmdist(train_set',M,'RegularizationValue',1e-10); alpha = GMModel.ComponentProportion; mu = (GMModel.mu)'; sigma = GMModel.Sigma; % Calculate log-likelihood performance with new parameters perf_array(b,m) = sum(log(evalGMM(val_set,alpha,mu,sigma))); end end % Calculate average performance for each M and find best fit avg_perf = sum(perf_array)/B; best_GMM = find(avg_perf == max(avg_perf),1);end
function [alpha_est,mu,Sigma]=EMforGMM(M, x, N,val_set)
% Uses EM algorithm to estimate the parameters of a GMM that has M
% number of components based on pre-existing training data of size Ndelta = 0.04; % tolerance for EM stopping criterion reg_weight = 1e-2; % regularization parameter for covariance estimates d = size(x,1); % dimensionality of data % Start with equal alpha estimates alpha_est = ones(1,M)/M; % Set initial mu as random M value pairs from data array shuffledIndices = randperm(N); mu = x(:,shuffledIndices(1:M)); % Assign each sample to the nearest mean [~,assignedCentroidLabels] = min(pdist2(mu',x'),[],1); % Use sample covariances of initial assignments as initial covariance estimates for m = 1:M Sigma(:,:,m) = cov(x(:,find(assignedCentroidLabels==m))') + reg_weight*eye(d,d); end % Run EM algorith until it converges t = 0; Converged = 0; while ~Converged % Calculate GMM distribution according to parameters for l = 1:M temp(l,:) = repmat(alpha_est(l),1,N).*evalGaussian(x,mu(:,l),Sigma(:,:,l)); end pl_given_x = temp./sum(temp,1); % Calculate new alpha values alpha_new = mean(pl_given_x,2); % Clculate new mu values w = pl_given_x./repmat(sum(pl_given_x,2),1,N); mu_new = x*w'; % Calculate new Sigma values for l = 1:M v = x-repmat(mu_new(:,l),1,N); u = repmat(w(l,:),d,1).*v; Sigma_new(:,:,l) = u*v' + reg_weight*eye(d,d); % adding a small regularization term end % Change in each parameter Dalpha = sum(abs(alpha_new-alpha_est')); Dmu = sum(sum(abs(mu_new-mu))); DSigma = sum(sum(abs(abs(Sigma_new-Sigma)))); % Check if converged Converged = ((Dalpha+Dmu+DSigma)<delta); % Update old parameters alpha_est = alpha_new; mu = mu_new; Sigma = Sigma_new; %log_lik = sum(log(evalGMM(val_set,alpha_est,mu,Sigma))) %Converged = (log_lik<-2.3); t = t+1; endend
function g = evalGaussian(x,mu,Sigma)
% Evaluates the Gaussian pdf N(mu,Sigma) at each coumn of X
[n,N] = size(x);
invSigma = inv(Sigma);
C = (2pi)^(-n/2) * det(invSigma)^(1/2);
E = -0.5sum((x-repmat(mu,1,N)).(invSigma(x-repmat(mu,1,N))),1);
g = C*exp(E);
end
function gmm = evalGMM(x,alpha,mu,Sigma)
% Evaluates GMM on the grid based on parameter values given
gmm = zeros(1,size(x,2));
for m = 1:length(alpha)
gmm = gmm + alpha(m)*evalGaussian(x,mu(:,m),Sigma(:,:,m));
end
end