数值计算系列之牛顿插值原理及实现

前言

本文介绍了插值概念和一般的计算方法，介绍了用于简化插值函数计算的牛顿插值方法。最后给出牛顿向前插值算法的python实现。

若您在阅读的过程中发现任何问题, 邮箱联系我: devecor@163.com

所谓插值？

假定存在一个未知函数 y=f(x) ,已知若干个点处的函数值：

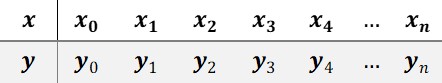
f(x)满足上述数据，但是满足上述数据的函数有无数个，没有办法从这一组数据中准确的得出f(x)

所谓插值，就是找到一个满足上述数据的足够好的函数，来代表或者近似f(x)，笔者将这样的一个插值函数记为\phi(x)

什么是足够好的函数？

一个足够好的近似函数\phi(x)，应当具备以下特点：

形式简单
容易计算
足够好的性态，即具有足够高阶的导数（连续优于间断，可导优于连续）

具有这样的特点的函数，通常是一类函数，比如多项式。

计算插值函数

确定一个函数类作为未知函数f(x)的近似函数。这个函数类可以是多项式，可以是三角函数，也可以是任何你认为具有上述特点的某一类函数。
从这个函数类中找到一个满足\phi(x_i)=y_i(i=1,2,...n)条件的函数\phi(x)作为这组数据的插值函数。前述条件称为插值条件，这些数据称为插值节点

多项式插值

一旦我们选定了一个函数类，就能知道所求的插值函数具有怎样的形式。比如选定多项式作为近似函数，使用下面的数据：

该组数据一共有n+1个插值节点，也就是说具有n+1个插值条件，要使这些插值条件同时得到满足，只能使用n次多项式作为插值函数，显然这样的插值函数具有以下形式：

y=a_0+a_1x+a_2x^2+\cdots +a_nx^n

根据插值条件，接下列方程即可

容易证明只要插值节点互不相同，上述方程必然有唯一解。

那么，问题来了，你愿不愿意求解上述的方程组呢？假如有2000条数据，即有2000个方程的高次方程组，你解过这么大的吗？或者说这种方法是有效的吗？

简化计算：牛顿插值

假定只有一个插值节点，那么数据看起来像这样

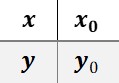
只有一个数据的插值函数记为\phi_0(x),要满足插值条件，插值函数显然是

\phi_0(x)=y_0

增加一个插值节点，数据像这样：

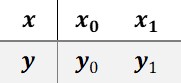
插值函数记为\phi_1(x)可以写成下面的形式：

\phi_2(x)=y_0+a_1(x-x_0)

上式满足第一个插值节点，a_1未知，将第二个插值节点代入，求得

a_1=\frac{y_1-y_0}{x_1-x_0}=\frac{y_1-\phi_0(x_1)}{x_1-x_0}

再增加一个插值节点，数据：

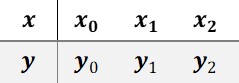
插值函数\phi_3(x)=y_0+a_1(x-x_0)+a_2(x-x_0)(x-x_1)

上式满足前两个插值节点，a_2未知，代入第三个插值节点，求得a_2=\frac{y_2-\left[y_0+a_1(x_2-x_0)\right]}{(x_2-x_0)(x_2-x_1)}=\frac{y_2-\phi_1(x_2)}{(x_2-x_0)(x_2-x_1)}

一般的，

a_i=\frac{y_i-\phi_{i-1}(x_i)}{(x-x_0)(x-x_1)\cdots(x-x_{i-1})}

那么，

\phi_n(x) = y_0+a_1(x-x_0)+a_2(x-x_0)(x-x_1)+\cdots+a_n(x-x_0)(x-x_1)\cdots(x-x_{n-1})

非等距节点牛顿插值的python实现

若插值节点是等距的，则可以使用向前差分极大的简化运算。不失一般性，本文基于递归实现非等距节点的牛顿插值算法。

功能设计

Newton插值算法极大的简化了计算，相对于Lagrange插值，最大的优势在于其具有计算的继承性。所谓继承性是指当增加一条数据，不必与原有数据一起重新计算插值函数，而是在原有的插值函数上增加一项，得出新的插值函数。基于此我们的算法应有下面的几个功能：

数据的输入
数据的更新
计算插值函数，保存计算结果

所以，新建pyiplt.py文件，写下如下代码

代码语言：txt

复制

class Interpolate(object):
    """Newton 插值函数类"""
    def __init__(self, data):
        pass
def update(self, data):
    pass

def interpolate(self):
    &#34;&#34;&#34;计算插值函数&#34;&#34;&#34;
    pass</code></pre></div></div><h5 id="5e9mq" name="%E6%95%B0%E6%8D%AE%E7%9A%84%E8%BE%93%E5%85%A5%E5%92%8C%E5%AD%98%E5%9C%A8%E5%BD%A2%E5%BC%8F">数据的输入和存在形式</h5><p>首先需要定义数据输入为nx2的numpy数组，为使用方便对<code>__init__()</code>函数做如下改动, 并定义数据的getter:</p><div class="rno-markdown-code"><div class="rno-markdown-code-toolbar"><div class="rno-markdown-code-toolbar-info"><div class="rno-markdown-code-toolbar-item is-type"><span class="is-m-hidden">代码语言：</span>txt</div></div><div class="rno-markdown-code-toolbar-opt"><div class="rno-markdown-code-toolbar-copy"><i class="icon-copy"></i><span class="is-m-hidden">复制</span></div></div></div><div class="developer-code-block"><pre class="prism-token token line-numbers language-txt"><code class="language-txt" style="margin-left:0">class Interpolate(object):

def __init__(self, data=None, x=None, y=None):
    pass

@property
def data(self):
    return self.__data</code></pre></div></div><p>新建 <code>test_pyiplt.py</code>文件</p><p>测试输入数据存在形式, 写下单元测试：</p><div class="rno-markdown-code"><div class="rno-markdown-code-toolbar"><div class="rno-markdown-code-toolbar-info"><div class="rno-markdown-code-toolbar-item is-type"><span class="is-m-hidden">代码语言：</span>txt</div></div><div class="rno-markdown-code-toolbar-opt"><div class="rno-markdown-code-toolbar-copy"><i class="icon-copy"></i><span class="is-m-hidden">复制</span></div></div></div><div class="developer-code-block"><pre class="prism-token token line-numbers language-txt"><code class="language-txt" style="margin-left:0">from unittest import TestCase

import numpy as np

from pyiplt import Interpolate
class TestInterpolate(TestCase):

x = [i for i in range(10)]

y = x.copy()

res = np.array([[i, i] for i in range(10)]).reshape((-1, 2))
def test_data(self):

    interpolator = Interpolate()
    self.assertIsNone(interpolator.data)

    interpolator = Interpolate(x=self.x, y=self.y)
    self.assertEqual(self.res.tolist(), interpolator.data.tolist())</code></pre></div></div><p>刚好能通过测试的代码：</p><div class="rno-markdown-code"><div class="rno-markdown-code-toolbar"><div class="rno-markdown-code-toolbar-info"><div class="rno-markdown-code-toolbar-item is-type"><span class="is-m-hidden">代码语言：</span>txt</div></div><div class="rno-markdown-code-toolbar-opt"><div class="rno-markdown-code-toolbar-copy"><i class="icon-copy"></i><span class="is-m-hidden">复制</span></div></div></div><div class="developer-code-block"><pre class="prism-token token line-numbers language-txt"><code class="language-txt" style="margin-left:0">import numpy as np

class Interpolate(object):
def __init__(self, data=None, x=None, y=None):

    if data is not None:
        self.__data = data
    elif x is not None and y is not None:
        assert len(x) == len(y), &#34;lengths isn&#39;t equal&#34;
        self.__data = np.array([[i, j] for i, j in zip(x, y)])\
            .reshape((-1, 2))
    else:
        self.__data = None

@property
def data(self):
    return self.__data</code></pre></div></div><h5 id="2kdgf" name="%E8%AE%A1%E7%AE%97%E6%8F%92%E5%80%BC%E5%87%BD%E6%95%B0">计算插值函数</h5><p>先写单元测试：</p><div class="rno-markdown-code"><div class="rno-markdown-code-toolbar"><div class="rno-markdown-code-toolbar-info"><div class="rno-markdown-code-toolbar-item is-type"><span class="is-m-hidden">代码语言：</span>txt</div></div><div class="rno-markdown-code-toolbar-opt"><div class="rno-markdown-code-toolbar-copy"><i class="icon-copy"></i><span class="is-m-hidden">复制</span></div></div></div><div class="developer-code-block"><pre class="prism-token token line-numbers language-txt"><code class="language-txt" style="margin-left:0">from unittest import TestCase

from pyiplt import Interpolate
class TestInterpolate(TestCase):
x = [i for i in range(10)]

y2 = [f(i) for i in x]
y3 = [f2(i) for i in x]

res2 = [1, 2, ] + [0 for _ in range(8)]    # 升幂排列
res3 = [2, 8, 3] + [0 for _ in range(7)]   # 升幂排列

def test_interpolate(self):

    interpolator = Interpolate()
    self.assertRaises(Exception, interpolator.interpolate)

    interpolator = Interpolate(x=self.x, y=self.y2)
    self.assertEqual(self.res2, interpolator.interpolate())

    interpolator2 = Interpolate(x=self.x, y=self.y3)
    self.assertEqual(self.res3, interpolator2.interpolate())</code></pre></div></div><p>在给出能够通过测试的代码之前，交代以下实现的思路：</p><p>根据Newton插值公式：</p><blockquote><p><span>\phi_n(x) = y_0+a_1(x-x_0)+a_2(x-x_0)(x-x_1)+\cdots+a_n(x-x_0)(x-x_1)\cdots(x-x_{n-1})</span>

 a_i=\frac{y_i-\phi_{i-1}(x_i)}{(x-x_0)(x-x_1)\cdots(x-x_{i-1})} 
我们知道，只需计算出a_0, a_1, ..., a_n就可以得到插值函数，但是a_n与前n个数据（n+1条数据）的插值函数有关，也就是与前面n个系数有关（你品，你细品），直到a_0，我们知道a_0 = y_0，只跟第一个插值节点相关。解决这种问题最常见的思维方式是自顶向下的模式，计算n+1个数据的插值函数时，先去计算前n个数据的插值函数，先计算前n-1个数据的插值函数，直到最后只有一个插值节点，写出这个节点的插值函数，然后依次回溯。这样的方式叫递归，通过对自身的调用化繁为简，最后逐步回溯。
代码语言：txt
复制
import numpy as np
def sub_mult(data):

"""

计算系数a_n分母处的连乘

:param data: 插值节点序列, [x0, x1, x2, x3, ..., x_n]

:return: (x_n - x_0) * (x_n - x_1) * ... * (x_n - x_{n-1})

"""

res = 1

loop_times = len(data) - 1

i = 0

while i < loop_times:

res *= (data[-1] - data[i])

i += 1

return res
class Interpolate(object):

"""Newton插值函数类

非等距节点的Newton插值的递归实现

:param data: array_like: [[x1, y1], [x2, y2], ...]

:param x: 插值节点序列

:param y: 对应函数值序列

"""
def __init__(self, data=None, x=None, y=None):
    if data is not None:
        self.__data = data
    elif x is not None and y is not None:
        assert len(x) == len(y), &#34;lengths isn&#39;t equal&#34;
        self.__data = np.array([[i, j] for i, j in zip(x, y)])\
            .reshape((-1, 2))
    else:
        self.__data = None

    # 插值结果的系数列表
    self.__coefficients = []

def interpolate(self):
    &#34;&#34;&#34;
    计算插值函数, 返回系数列表
    :return: list 多项式插值函数系数列表，按升幂排列
    &#34;&#34;&#34;
    if self.__data is None or len(self.__data) == 0:
        raise Exception(&#34;NoneDataError: please update first, use &#39;self.update&#39;&#34;)
    self.__factor(self.__data)
    return self.__coefficients

def __factor(self, data):
    &#34;&#34;&#34;
    自顶向下递归的计算插值函数的系数
    :param data:
    :return:
    &#34;&#34;&#34;
    x = [i[0] for i in data]
    if data.shape[0] == 1:
        self.__coefficients.append(data[0][1])
        return
    self.__factor(data[0:-1])
    self.__coefficients.append(
        (data[-1][1] - self.__phi(x)) / sub_mult(x)
    )

def __phi(self, data):
    &#34;&#34;&#34;
    计算f_{n-1}(x_n)的值
    :param data: [x_0, x_1, ..., x_n]
    :return:
    &#34;&#34;&#34;
    assert len(data) &gt;= 2, &#34;assertFail: length &lt; 2!!!&#34;
    res = self.__coefficients[0]
    if len(data) &gt; 2:
        loop_times = len(data[0:-2])
        i = 0
        while i &lt; loop_times:
            temp = 1
            j = 0
            while j &lt;= i:
                temp *= (data[-1] - data[j])
                j += 1

            res += self.__coefficients[i+1] * temp
            i += 1
    return res</code></pre></div></div><p>下面是完整版的代码，比前文更完善，请读者细品</p><p>单元测试：</p><div class="rno-markdown-code"><div class="rno-markdown-code-toolbar"><div class="rno-markdown-code-toolbar-info"><div class="rno-markdown-code-toolbar-item is-type"><span class="is-m-hidden">代码语言：</span>txt</div></div><div class="rno-markdown-code-toolbar-opt"><div class="rno-markdown-code-toolbar-copy"><i class="icon-copy"></i><span class="is-m-hidden">复制</span></div></div></div><div class="developer-code-block"><pre class="prism-token token line-numbers language-txt"><code class="language-txt" style="margin-left:0">import numpy as np

from unittest import TestCase

from pyiplt import Interpolate

from pyiplt import sub_mult
def f(x):

return 2 * x + 1
def f2(x):

return 2 + 5 * x + 3 * x ** 2
class TestInterpolate(TestCase):
x = [i for i in range(10)]
y = x.copy()

y2 = [f(i) for i in x]
y3 = [f2(i) for i in x]

res = np.array([[i, i] for i in range(10)]).reshape((-1, 2))
res2 = [1, 2, ] + [0 for _ in range(8)]    # 升幂排列
res3 = [2, 8, 3] + [0 for _ in range(7)]   # 升幂排列

def test_data(self):

    interpolator = Interpolate()
    self.assertIsNone(interpolator.data)

    interpolator = Interpolate(x=self.x, y=self.y)
    self.assertEqual(self.res.tolist(), interpolator.data.tolist())

def test_interpolate(self):

    interpolator = Interpolate()
    self.assertRaises(Exception, interpolator.interpolate)

    interpolator = Interpolate(x=self.x, y=self.y2)
    self.assertEqual(self.res2, interpolator.interpolate())

    interpolator2 = Interpolate(x=self.x, y=self.y3)
    self.assertEqual(self.res3, interpolator2.interpolate())

def test_iplt_f(self):
    interpolator = Interpolate(x=self.x, y=self.y2)
    interpolator.interpolate()
    res = [interpolator.iplt_f(i) for i in self.x]
    self.assertEqual(res, self.y2)

class Test(TestCase):

def test_sub_mult(self):

data1 = [1, 2, 3]

res1 = 2

data2 = [3, 6, 4]

res2 = -2

data3 = [8, 3, 5, 9]

res3 = 24

self.assertEqual(res1, sub_mult(data1))

self.assertEqual(res2, sub_mult(data2))

self.assertEqual(res3, sub_mult(data3))
可以通过测试的代码：
代码语言：txt
复制
import numpy as np
def sub_mult(data):

"""

计算系数a_n分母处的连乘

:param data: 插值节点序列, [x0, x1, x2, x3, ..., x_n]

:return: (x_n - x_0) * (x_n - x_1) * ... * (x_n - x_{n-1})

"""

res = 1

loop_times = len(data) - 1

i = 0

while i < loop_times:

res *= (data[-1] - data[i])

i += 1

return res
class Interpolate(object):

"""Newton插值函数类

非等距节点的Newton插值的递归实现

:param data: array_like: [[x1, y1], [x2, y2], ...]

:param x: 插值节点序列

:param y: 对应函数值序列

"""
def __init__(self, data=None, x=None, y=None):
    if data is not None:
        self.__data = data
    elif x is not None and y is not None:
        assert len(x) == len(y), &#34;lengths isn&#39;t equal&#34;
        self.__data = np.array([[i, j] for i, j in zip(x, y)])\
            .reshape((-1, 2))
    else:
        self.__data = None

    # 插值结果的系数列表
    self.__coefficients = []

@property
def data(self):
    return self.__data

def update(self, data=None, x=None, y=None):
    &#34;&#34;&#34;
    在现有数据上添加数据，返回更新后的插值结果，充分发挥Newton插值的优势
    :param data: array_like: [[x1, y1], [x2, y2], ...]
    :param x: 插值节点序列
    :param y: 对应函数值序列
    :return: list 多项式插值函数系数列表，按升幂排列
    &#34;&#34;&#34;

    # 拼接数据
    if data is not None:
        self.__data = np.concatenate((self.__data, data))
    elif x is not None and y is not None:
        assert len(x) == len(y), &#34;lengths isn&#39;t equal&#34;
        data = np.array([[i, j] for i, j in zip(x, y)])\
            .reshape((-1, 2))
        self.__data = np.concatenate((self.__data, data))

    # 更新插值函数
    i = data.shape[0]
    while i &gt; 0:
        if i-1 == 0:
            x = [i[0] for i in self.__data]
        else:
            x = [i[0] for i in self.__data[0:-(i-1)]]

        self.__coefficients.append(
            (self.__data[-(i-2)][1] - self.__phi(x)) / sub_mult(x)
        )
    return self.__coefficients

def interpolate(self):
    &#34;&#34;&#34;
    计算插值函数, 返回系数列表
    :return: list 多项式插值函数系数列表，按升幂排列
    &#34;&#34;&#34;
    if self.__data is None or len(self.__data) == 0:
        raise Exception(&#34;NoneDataError: please update first, use &#39;self.update&#39;&#34;)
    self.__factor(self.__data)
    return self.__coefficients

def __factor(self, data):
    &#34;&#34;&#34;
    自底向上递归的计算插值函数的系数
    :param data:
    :return:
    &#34;&#34;&#34;
    x = [i[0] for i in data]
    if data.shape[0] == 1:
        self.__coefficients.append(data[0][1])
        return
    self.__factor(data[0:-1])
    self.__coefficients.append(
        (data[-1][1] - self.__phi(x)) / sub_mult(x)
    )

def __phi(self, data):
    &#34;&#34;&#34;
    计算f_{n-1}(x_n)的值
    :param data: [x_0, x_1, ..., x_n]
    :return:
    &#34;&#34;&#34;
    assert len(data) &gt;= 2, &#34;assertFail: length &lt; 2!!!&#34;
    res = self.__coefficients[0]
    if len(data) &gt; 2:
        loop_times = len(data[0:-2])
        i = 0
        while i &lt; loop_times:
            temp = 1
            j = 0
            while j &lt;= i:
                temp *= (data[-1] - data[j])
                j += 1

            res += self.__coefficients[i+1] * temp
            i += 1
    return res

def iplt_f(self, x):
    &#34;&#34;&#34;计算好的插值函数&#34;&#34;&#34;
    if len(self.__coefficients) &gt; 0:
        res = 0
        for k, v in enumerate(self.__coefficients):
            i = 0
            temp = 1
            while i &lt; k:
                temp *= (x - self.__data[i][0])
                i += 1
            res += v * temp
        return res
    else:
        raise Exception(&#34;UserError: please call self.interpolate first&#34;)

def res2str(self):
    res = &#34;&#34;
    for i, e in enumerate(self.__coefficients):
        if i == 0:
            res += &#34; &#34; + str(e) + &#34;\n&#34;
        elif e &gt; 0:
            res += (&#34;+ &#34; + str(e) + &#34;x^&#34; + str(i) + &#34;\n&#34;)
        elif e &lt; 0:
            res += (&#34;- &#34; + str(-e) + &#34;x^&#34; + str(i) + &#34;\n&#34;)
    return res

if name == "main":
def f(x):
    return np.power(x, 2.6)

x = np.array([i/10 for i in range(20, 31)])
y = np.array([f(i) for i in x])

print(&#34;输入数据：&#34;)
print(&#34;x: {}&#34;.format(x))
print(&#34;y: {}&#34;.format(y))

interpolator = Interpolate(x=x, y=y)
coefficients = interpolator.interpolate()

print(&#34;插值函数:\n{}&#34;.format(interpolator.res2str()))

print(&#34;计算结果：&#34;)
print(&#34;2.34^2.6 = {}&#34;.format(interpolator.iplt_f(2.34)))
print(&#34;2.98^2.6 = {}&#34;.format(interpolator.iplt_f(2.98)))</code></pre></div></div><p>单元测试结果：</p><figure class=""><div class="rno-markdown-img-url" style="text-align:center"><div class="rno-markdown-img-url-inner" style="width:40.44%"><div style="width:100%"><img src="https://cdn.static.attains.cn/app/developer-bbs/upload/1723286386397360125.png" /></div><div class="figure-desc">image.png</div></div></div></figure><p>运行结果：</p><figure class=""><div class="rno-markdown-img-url" style="text-align:center"><div class="rno-markdown-img-url-inner" style="width:100%"><div style="width:100%"><img src="https://cdn.static.attains.cn/app/developer-bbs/upload/1723286386573570569.png" /></div><div class="figure-desc">image.png</div></div></div></figure>