标题:三维点云分割综述(中)
作者:Yuxing Xie, Jiaojiao Tian
摘要
在上篇文章中,我们介绍了关于点云的获取方式上的区别,点云的密度,以及各种场景下应用的区别,本篇文章将更加具体的介绍点云分割相关技术。
点云分割算法(PCS)主要基于从几何约束和统计规则出发制定的严格的人工设计的特征。PCS的主要过程是将原始3D点分组为非重叠区域。这些区域对应于一个场景中的特定结构或对象。由于这种分割过程不需要有监督的先验知识,因此所得到的结果没有很强的语义信息。这些方法可以分为四大类:
基于边缘的、基于区域增长的、基于模型拟合的和基于聚类的四种方法。
基于边缘的分割
基于边缘的PCS方法是将基于二维图像方法直接应用转换为三维点云,这种方法主要用于PCS的早期阶段,由于物体的形状是由边缘来描述的,因此可以通过寻找靠近边缘区域的点来解决PCS问题。基于边缘的方法的原理是定位亮度快速变化的点,这类似于一些二维图像分割方法。根据文献的定义,基于边缘的分割算法主要分为两个阶段:
(1)边缘检测,提取不同区域的边界;
(2)边缘点分组,通过对(1)中的边界内的点进行分组来生成最终的分割。
例如,在一些论文中,作者设计了一种基于梯度的边缘检测算法,将三维直线拟合到一组点上,并检测曲面上单位法向量方向的变化。在文献中,作者提出了一种基于高级分割基元(曲线段)的快速分割方法,可以显著减少数据量。与文献中提出的方法相比,该算法既精确又高效,但它只适用于距离图像,可能不起作用。(具体文献可以查看原文)
对于密度不均匀的点云。此外,文[141]还从二值边缘图中提取出闭合轮廓,以实现快速分割。[142]介绍了一种基于并行边缘的分割算法,提取了三种类型的边缘。该算法采用了可重构多环网络的算法优化机制,减少了算法运行时间。
基于边缘的算法由于其简单性,使得pc机能够快速运行,但只有在提供具有理想点的简单场景(如低噪声、均匀密度)时才能保持良好的性能。其中有些方法仅适用于深度图像而不适用于三维点。因此,这种方法目前很少应用于密集和/或大面积的点云数据集。此外,在三维空间中,这种方法通常会产生不连续的边缘,不需要填充或解释程序,就不能直接用于识别闭合段。
基于区域增长的分割
区域生长是一种经典的PCS方法,至今仍被广泛应用。它将两个点或两个区域单元之间的特征相结合,以测量像素(2D)、点(3D)或体素(3D)之间的相似性,并将它们合并在一起(如果它们在空间上接近并且具有相似的表面特性)。Besl和Jain[144]提出了两步初始算法:
(1)粗分割,根据每个点及其符号的平均曲率和高斯曲率选择种子像素;
(2)区域生长,在区域生长中,基于可变阶二元曲面拟合,使用交互区域生长来细化步骤(1)的结果。
最初,这种方法主要用于二维分割。在PCS研究的早期阶段,大多数点云实际上是2.5D机载激光雷达数据,其中只有一层在z方向有视野,一般的预处理步骤是将点从三维空间转换为二维栅格域[145]。随着更容易获得的真实三维点云,区域增长很快被直接应用于三维空间。这种三维区域生长技术已广泛应用于建筑平面结构的分割[75]、[93]。
与二维情况类似,三维区域生长包括两个步骤:
(1)选择种子点或种子单元;
(2)区域生长,由一定的原则驱动。在设计区域生长算法时,需要考虑三个关键因素:相似性度量、生长单元和种子点选择。
对于标准因子,通常使用几何特征,例如欧几里德距离或法向量。例如,Ning等人。[106]以法向量为判据,使得共面可以共享相同的法向。Tovari等人。[146]应用法向量、相邻点到调整平面的距离以及当前点和候选点之间的距离作为将点合并到种子区域的标准,该种子区域是在手动过滤边缘附近区域后从数据集中随机选取的。Dong等人。[104]选择法向量和两个单位之间的距离。
对于生长单元因子,通常有三种策略:
(1)单点;
(2)区域单元,如体素网格和八叉树结构;
(3)混合单元。
在早期阶段,选择单点作为区域单位是主要的方法[106],[138]。然而,对于海量点云,逐点计算非常耗时。为了减少原始点云的数据量,提高计算效率,例如在原始数据中用k-d树进行邻域搜索[147],区域单元是三维区域生长中直接点的替代思想。在点云场景中,体素化单元的数量小于点的数量。这样,区域发展进程就可以大大加快。在这种策略的指导下,Deschaud等人。[147]提出了一种基于体素的区域生长算法,通过在区域生长过程中用体素代替点来提高效率。Vo等人。[93]提出了一种基于八叉树的自适应区域生长算法,通过对具有相似显著性特征的相邻体素进行增量分组来实现快速曲面片分割。作为精度和效率的平衡,混合单元也被提出并通过一些研究进行了测试。例如,肖等。[101]结合单点和子窗口作为生长单元来检测平面。Dong等人。[104]采用基于单点和超体素单元的混合区域生长算法,在全局能量优化之前实现粗分割。
对于种子点的选择,由于许多区域生长算法都是以平面分割为目标,通常的做法是先为某个点及其相邻点设计一个拟合平面,然后选择对拟合平面残差最小的点作为种子点[106],[138]。残差通常由一个点与其拟合平面之间的距离[106]、[138]或点的曲率来估计。非均匀性是区域增长的一个重要问题[93]。这些算法的精度依赖于种子的生长准则和位置,它们应该根据不同的数据集进行预定义和调整。此外,这些算法计算量大,可能需要减少数据量,以便在精度和效率之间进行权衡。
基于模型拟合分割
模型拟合的核心思想是将点云与不同的原始几何图形进行匹配,通常被认为是一种形状检测或提取方法。但是,当处理具有参数几何图形/模型的场景时,例如平面、球体和圆柱体,模型拟合。
也可以看作是一种分割方法。最常用的模型拟合方法是建立在两种经典算法上的,Hough变换(HT)和随机样本一致性(RANSAC)。
HT:HT是数字图像处理中一种经典的特征检测技术。它最初在[148]中提出,用于二维图像中的直线检测。HT[149]有三个主要步骤:
(1)将原始空间的每个样本(例如,二维图像中的像素和点云中的点)映射到离散化的参数空间中;
(2)在参数空间上放置一个带有单元格数组的累加器,然后对每个输入样本进行投票
(3)选取局部得分最大的单元,用参数坐标表示原始空间中的一个几何段。HT最基本的形式是广义Hough变换(GHT),也称为标准Hough变换(SHT),它是在[150]中引入的。
RANSAC:RANSAC技术是另一种流行的模型拟合方法[158]。一些关于基于RANSAC的方法已经发表。强烈建议您进一步了解RANSAC家族及其效果,尤其是在[159]-[161]中。基于RANSAC的算法有两个主要阶段:(1)从随机样本中生成假设(假设生成)和(2)对数据进行验证(假设评估/模型验证)[159],[160]。在步骤(1)之前,与基于HT的方法一样,必须手动定义或选择模型。根据3D场景的结构,在pc机中,这些通常是平面、球体或其他可以用代数公式表示的几何图元。
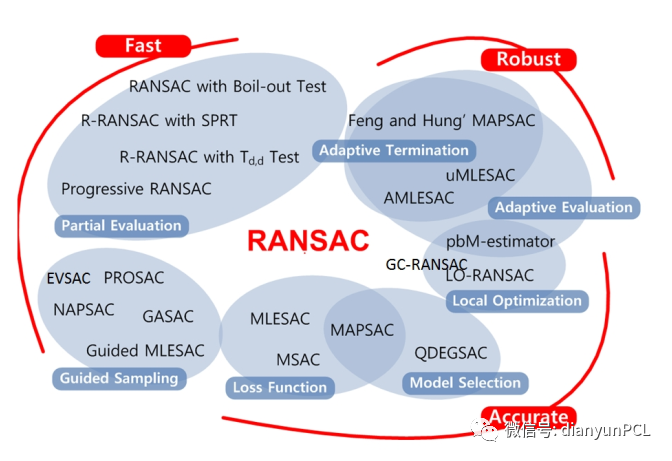
RANSAC族,算法根据其性能和基本策略分类
基于聚类分割
基于聚类的方法广泛应用于无监督PCS任务。严格地说,基于聚类的方法不是基于特定的数学理论。该方法是具有相同目标的不同方法的混合,即将具有相似几何谱特征或空间分布的点组合成相同的均匀模式。与区域生长和模型拟合不同,这些模式通常没有预先定义[166],因此基于聚类的算法可用于不规则对象分割,例如植被。此外,与区域生长方法相比,基于聚类的方法不需要种子点[109]。在早期,K均值[45]、[46]、[76]、[77]、[91]、均值偏移[47]、[48]、[80]、[92]和模糊聚类[77]、[105]是基于聚类的点云分割家族中的主要算法。对于每种聚类方法,可以选择具有不同特征的几个相似性度量,包括欧几里德距离、密度和法向量[109]。从数学和统计学的角度来看,聚类问题可以看作是一个基于图的优化问题,因此在PCS[78]、[79]、[167]中尝试了几种基于图的方法
1)K-means:K-means是一种基本的、广泛应用的无监督聚类分析算法。它将点云数据集分为K个未标记类。K-means聚类中心不同于区域生长的种子点。在K-means算法中,在每一步迭代过程中,每一个点都要与每一个聚类中心进行比较,当吸收一个新的点时,聚类中心会发生变化。K-means的过程是“聚类”而不是“增长”。它已被用于ALS数据的单树冠分割[91]和屋顶的平面结构提取[76]。Shahzad等人。[45]朱等。[46]利用K-均值在TomoSAR点云上建立fac¸ade分割。K-means的一个优点是它可以很容易地适应各种特征属性,甚至可以用于多维特征空间。K-means的主要缺点是有时很难正确地预先定义K的值
2)模糊聚类:模糊聚类算法是K-means的改进版本。K-means是一种硬聚类方法,即样本点对聚类中心的权重为1或0。相比之下,模糊方法使用软聚类,这意味着一个样本点可以属于多个具有一定非零权重的聚类。文献[105]将模糊C-均值(FCM)算法和可能性C-均值(PCM)两种模糊算法相结合,提出了一种无初始化框架。该框架在三点云上进行了测试,包括一个单扫描TLS室外数据集和建筑结构。实验表明,模糊聚类分割在平面曲面上具有良好的分割效果。Sampath等人。[77]利用模糊K-均值从ALS点云分割和重建建筑物屋顶。
3) Mean-shift:与K-means相比,Mean-shift是一种经典的非参数聚类算法,因此避免了K-means[168]–[170]中预定义的K问题。它已被有效地应用于城市和森林地形的ALS数据[80],[92]。也采用了单点云[48]的平均值,使之能在同一个点上移动。由于簇数目和每个簇的形状都是未知的,所以均值偏移产生了高概率的过分段结果[81]。因此,它通常被用作分区或优化之前的一个预分段步骤。
4) 基于图优化:在2D计算机视觉中,引入图形来表示像素或超像素等数据单元已被证明是一种有效的分割策略。在这种情况下,分割问题可以转化为图的构造和划分问题。受2D中基于图的方法的启发,一些研究将相似的策略应用到PCS中,并在不同的数据集中取得了结果。例如,Golovinskiy和Funkhouser[167]提出了一种基于最小割集的PCS算法[171],通过使用k近邻构造一个图。min-cut被成功地应用于室外城市目标检测[167]。[78]还使用最小割来解决ALS-PCS的能量最小化问题,每个点都被认为是图中的一个节点,每个节点通过一条边与其3D voronoi邻域相连。
马尔可夫随机场(MRF)和条件随机场(CRF)是解决基于图的分割问题的机器学习方法。它们通常被用作pcs的监督方法或后处理阶段。使用CRF和监督MRF的主要研究属于PCS而不是PCS。有关监督方法的更多信息,将在三维点云分割综述(下)文章中介绍。
过度分割、超体素和预分割
为了降低计算成本和噪声带来的负面影响,一种常用的策略是在应用计算量大的算法之前将原始点云过度分割成小区域。体素可以看作是最简单的过分割结构。与二维图像中的超像素类似,超体素是感知上相似体素的小区域。由于超体素可以大幅度减少原始点云的数据量,且信息损失小,重叠最小,因此通常使用超体素。
在执行其他计算开销较大的算法之前进行的预分片。一旦超分割(如超体素)被生成,这些超分割将被输入到后处理的PCS算法而不是初始点。最经典的点云过分割算法是体素云连通性分割(VCCS)[173]。该方法首先对点云进行八叉树体素化。然后采用K均值聚类算法实现超体素分割。然而,由于VCCS采用固定的分辨率,并且依赖于种子点的初始化,在非均匀密度下分割边界的质量无法得到保证。
参考文献
向上滑动阅览
[52] S. Gernhardt, N. Adam, M. Eineder, and R. Bamler, “Potential of very high resolution sar for persistent scatterer interferometry in
urban areas,” Annals of GIS, vol. 16, no. 2, pp. 103–111, 2010.
[53] S. Gernhardt, X. Cong, M. Eineder, S. Hinz, and R. Bamler, “Geometrical fusion of multitrack ps point clouds,” IEEE Geoscience
and Remote Sensing Letters, vol. 9, no. 1, pp. 38–42, 2012.
[54] X. X. Zhu and R. Bamler, “Super-resolution power and robustness of compressive sensing for spectral estimation with application to
spaceborne tomographic sar,” IEEE Transactions on Geoscience and Remote Sensing, vol. 50, no. 1, pp. 247–258, 2012.
[55] S. Montazeri, F. Rodr´ıguez Gonzalez, and X. X. Zhu, “Geocoding error correction for insar point clouds,” ´ Remote Sensing, vol. 10,
no. 10, p. 1523, 2018.
[56] F. Rottensteiner and C. Briese, “A new method for building extraction in urban areas from high-resolution lidar data,” in International
Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, vol. 34, pp. 295–301, 2002.
[57] X. X. Zhu and R. Bamler, “Demonstration of super-resolution for tomographic sar imaging in urban environment,” IEEE Transactions
on Geoscience and Remote Sensing, vol. 50, no. 8, pp. 3150–3157, 2012.
[58] X. X. Zhu, M. Shahzad, and R. Bamler, “From tomosar point clouds to objects: Facade reconstruction,” in 2012 Tyrrhenian Workshop
on Advances in Radar and Remote Sensing (TyWRRS), pp. 106–113, IEEE, 2012.
[59] X. X. Zhu and R. Bamler, “Let’s do the time warp: Multicomponent nonlinear motion estimation in differential sar tomography,”
IEEE Geoscience and Remote Sensing Letters, vol. 8, no. 4, pp. 735–739, 2011.
[60] S. Auer, S. Gernhardt, and R. Bamler, “Ghost persistent scatterers related to multiple signal reflections,” IEEE Geoscience and Remote
Sensing Letters, vol. 8, no. 5, pp. 919–923, 2011.
[61] Y. Shi, X. X. Zhu, and R. Bamler, “Nonlocal compressive sensing-based sar tomography,” IEEE Transactions on Geoscience and
Remote Sensing, vol. 57, no. 5, pp. 3015–3024, 2019.
[62] Y. Wang and X. X. Zhu, “Automatic feature-based geometric fusion of multiview tomosar point clouds in urban area,” IEEE Journal
of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 8, no. 3, pp. 953–965, 2014.
[63] M. Schmitt and X. X. Zhu, “Data fusion and remote sensing: An ever-growing relationship,” IEEE Geoscience and Remote Sensing
Magazine, vol. 4, no. 4, pp. 6–23, 2016.
[64] Y. Wang, X. X. Zhu, B. Zeisl, and M. Pollefeys, “Fusing meter-resolution 4-d insar point clouds and optical images for semantic
urban infrastructure monitoring,” IEEE Transactions on Geoscience and Remote Sensing, vol. 55, no. 1, pp. 14–26, 2017.
[65] A. Adam, E. Chatzilari, S. Nikolopoulos, and I. Kompatsiaris, “H-ransac: A hybrid point cloud segmentation combining 2d and 3d
data.,” ISPRS Annals of Photogrammetry, Remote Sensing & Spatial Information Sciences, vol. 4, no. 2, 2018.
[66] J. Bauer, K. Karner, K. Schindler, A. Klaus, and C. Zach, “Segmentation of building from dense 3d point-clouds,” in Proceedings of
the ISPRS. Workshop Laser scanning Enschede, pp. 12–14, 2005.
[67] A. Boulch, J. Guerry, B. Le Saux, and N. Audebert, “Snapnet: 3d point cloud semantic labeling with 2d deep segmentation networks,”
Computers & Graphics, vol. 71, pp. 189–198, 2018.
[68] H. Su, V. Jampani, D. Sun, S. Maji, E. Kalogerakis, M.-H. Yang, and J. Kautz, “Splatnet: Sparse lattice networks for point cloud
processing,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 2530–2539, 2018.
[69] G. Riegler, A. Osman Ulusoy, and A. Geiger, “Octnet: Learning deep 3d representations at high resolutions,” in Proceedings of the
IEEE Conference on Computer Vision and Pattern Recognition, pp. 3577–3586, 2017.
[70] C. Choy, J. Gwak, and S. Savarese, “4d spatio-temporal convnets: Minkowski convolutional neural networks,” in Proceedings of the
IEEE Conference on Computer Vision and Pattern Recognition, pp. 3075–3084, 2019.
[71] F. A. Limberger and M. M. Oliveira, “Real-time detection of planar regions in unorganized point clouds,” Pattern Recognition, vol. 48,
no. 6, pp. 2043–2053, 2015.
[72] B. Xu, W. Jiang, J. Shan, J. Zhang, and L. Li, “Investigation on the weighted ransac approaches for building roof plane segmentation
from lidar point clouds,” Remote Sensing, vol. 8, no. 1, p. 5, 2015.
[73] D. Chen, L. Zhang, P. T. Mathiopoulos, and X. Huang, “A methodology for automated segmentation and reconstruction of urban 3-d
buildings from als point clouds,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 7, no. 10,
pp. 4199–4217, 2014.
[74] F. Tarsha-Kurdi, T. Landes, and P. Grussenmeyer, “Hough-transform and extended ransac algorithms for automatic detection of 3d
building roof planes from lidar data,” in ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, vol. 36, pp. 407–412, 2007.
[75] B. Gorte, “Segmentation of tin-structured surface models,” in International Archives of Photogrammetry Remote Sensing and Spatial
Information Sciences, vol. 34, pp. 465–469, 2002.
[76] A. Sampath and J. Shan, “Clustering based planar roof extraction from lidar data,” in American Society for Photogrammetry and
Remote Sensing Annual Conference, Reno, Nevada, May, pp. 1–6, 2006.
[77] A. Sampath and J. Shan, “Segmentation and reconstruction of polyhedral building roofs from aerial lidar point clouds,” IEEE
Transactions on geoscience and remote sensing, vol. 48, no. 3, pp. 1554–1567, 2010.
[78] S. Ural and J. Shan, “Min-cut based segmentation of airborne lidar point clouds,” in International Archives of the Photogrammetry,
Remote Sensing and Spatial Information Sciences, pp. 167–172, 2012.
[79] J. Yan, J. Shan, and W. Jiang, “A global optimization approach to roof segmentation from airborne lidar point clouds,” ISPRS journal
of photogrammetry and remote sensing, vol. 94, pp. 183–193, 2014.
[80] T. Melzer, “Non-parametric segmentation of als point clouds using mean shift,” Journal of Applied Geodesy Jag, vol. 1, no. 3,
pp. 159–170, 2007.
[81] W. Yao, S. Hinz, and U. Stilla, “Object extraction based on 3d-segmentation of lidar data by combining mean shift with normalized
cuts: Two examples from urban areas,” in 2009 Joint Urban Remote Sensing Event, pp. 1–6, IEEE,
[82] S. K. Lodha, D. M. Fitzpatrick, and D. P. Helmbold, “Aerial lidar data classification using adaboost,” in Sixth International Conference
on 3-D Digital Imaging and Modeling (3DIM 2007), pp. 435–442, IEEE, 2007.
[83] M. Carlberg, P. Gao, G. Chen, and A. Zakhor, “Classifying urban landscape in aerial lidar using 3d shape analysis,” in 2009 16th
IEEE International Conference on Image Processing (ICIP), pp. 1701–1704, IEEE, 2009.
[84] N. Chehata, L. Guo, and C. Mallet, “Airborne lidar feature selection for urban classification using random forests,” in International
Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, vol. 38, pp. 207–212, 2009.
[85] R. Shapovalov, E. Velizhev, and O. Barinova, “Nonassociative markov networks for 3d point cloud classification,” in International
Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, vol. 38, pp. 103–108, 2010.
[86] J. Niemeyer, F. Rottensteiner, and U. Soergel, “Conditional random fields for lidar point cloud classification in complex urban areas,”
in ISPRS annals of the photogrammetry, remote sensing and spatial information sciences, vol. 3, pp. 263–268, 2012.
[87] J. Niemeyer, F. Rottensteiner, and U. Soergel, “Contextual classification of lidar data and building object detection in urban areas,”
ISPRS journal of photogrammetry and remote sensing, vol. 87, pp. 152–165, 2014.
[88] G. Vosselman, M. Coenen, and F. Rottensteiner, “Contextual segment-based classification of airborne laser scanner data,” ISPRS
journal of photogrammetry and remote sensing, vol. 128, pp. 354–371, 2017.
[89] X. Xiong, D. Munoz, J. A. Bagnell, and M. Hebert, “3-d scene analysis via sequenced predictions over points and regions,” in 2011
IEEE International Conference on Robotics and Automation, pp. 2609–2616, IEEE, 2011.
[90] M. Najafi, S. T. Namin, M. Salzmann, and L. Petersson, “Non-associative higher-order markov networks for point cloud classification,”
in European Conference on Computer Vision, pp. 500–515, Springer, 2014.
[91] F. Morsdorf, E. Meier, B. Kotz, K. I. Itten, M. Dobbertin, and B. Allg ¨ ower, “Lidar-based geometric reconstruction of boreal type forest ¨
stands at single tree level for forest and wildland fire management,” Remote Sensing of Environment, vol. 92, no. 3, pp. 353–362,
2004.
[92] A. Ferraz, F. Bretar, S. Jacquemoud, G. Gonc¸alves, and L. Pereira, “3d segmentation of forest structure using a mean-shift based
algorithm,” in 2010 IEEE International Conference on Image Processing, pp. 1413–1416, IEEE, 2010.
[93] A.-V. Vo, L. Truong-Hong, D. F. Laefer, and M. Bertolotto, “Octree-based region growing for point cloud segmentation,” ISPRS
Journal of Photogrammetry and Remote Sensing, vol. 104, pp. 88–100, 2015.
[94] A. Nurunnabi, D. Belton, and G. West, “Robust segmentation in laser scanning 3d point cloud data,” in 2012 International Conference
on Digital Image Computing Techniques and Applications (DICTA), pp. 1–8, IEEE, 2012.
[95] M. Weinmann, B. Jutzi, S. Hinz, and C. Mallet, “Semantic point cloud interpretation based on optimal neighborhoods, relevant features
and efficient classifiers,” ISPRS Journal of Photogrammetry and Remote Sensing, vol. 105, pp. 286–304, 2015.
[96] D. Munoz, J. A. Bagnell, N. Vandapel, and M. Hebert, “Contextual classification with functional max-margin markov networks,” in
2009 IEEE Conference on Computer Vision and Pattern Recognition, pp. 975–982, IEEE, 2009.
[97] L. Landrieu, H. Raguet, B. Vallet, C. Mallet, and M. Weinmann, “A structured regularization framework for spatially smoothing
semantic labelings of 3d point clouds,” ISPRS Journal of Photogrammetry and Remote Sensing, vol. 132, pp. 102–118, 2017
[98] L. Tchapmi, C. Choy, I. Armeni, J. Gwak, and S. Savarese, “Segcloud: Semantic segmentation of 3d point clouds,” in 2017 International
Conference on 3D Vision (3DV), pp. 537–547, IEEE, 2017.
[99] X. Ye, J. Li, H. Huang, L. Du, and X. Zhang, “3d recurrent neural networks with context fusion for point cloud semantic segmentation,”
in Proceedings of the European Conference on Computer Vision (ECCV), pp. 403–417, 2018.
[100] L. Landrieu and M. Boussaha, “Point cloud oversegmentation with graph-structured deep metric learning,” in Proceedings of the IEEE
Conference on Computer Vision and Pattern Recognition, pp. 7440–7449, 2019.
[101] J. Xiao, J. Zhang, B. Adler, H. Zhang, and J. Zhang, “Three-dimensional point cloud plane segmentation in both structured and
unstructured environments,” Robotics and Autonomous Systems, vol. 61, no. 12, pp. 1641–1652, 2013.
[102] L. Li, F. Yang, H. Zhu, D. Li, Y. Li, and L. Tang, “An improved ransac for 3d point cloud plane segmentation based on normal
distribution transformation cells,” Remote Sensing, vol. 9, no. 5, p. 433, 2017.
[103] H. Boulaassal, T. Landes, P. Grussenmeyer, and F. Tarsha-Kurdi, “Automatic segmentation of building facades using terrestrial laser
data,” in ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, pp. 65–70, 2007.
[104] Z. Dong, B. Yang, P. Hu, and S. Scherer, “An efficient global energy optimization approach for robust 3d plane segmentation of point
clouds,” ISPRS Journal of Photogrammetry and Remote Sensing, vol. 137, pp. 112–133, 2018.
[105] J. M. Biosca and J. L. Lerma, “Unsupervised robust planar segmentation of terrestrial laser scanner point clouds based on fuzzy
clustering methods,” ISPRS Journal of Photogrammetry and Remote Sensing, vol. 63, no. 1, pp. 84–98, 2008.
[106] X. Ning, X. Zhang, Y. Wang, and M. Jaeger, “Segmentation of architecture shape information from 3d point cloud,” in Proceedings
of the 8th International Conference on Virtual Reality Continuum and its Applications in Industry, pp. 127–132, ACM, 2009.
[107] Y. Xu, S. Tuttas, and U. Stilla, “Segmentation of 3d outdoor scenes using hierarchical clustering structure and perceptual grouping
laws,” in 2016 9th IAPR Workshop on Pattern Recogniton in Remote Sensing (PRRS), pp. 1–6, IEEE, 2016.
[108] Y. Xu, L. Hoegner, S. Tuttas, and U. Stilla, “Voxel-and graph-based point cloud segmentation of 3d scenes using perceptual grouping
laws,” in ISPRS Annals of Photogrammetry, Remote Sensing & Spatial Information Sciences, vol. 4, 2017.
[109] Y. Xu, W. Yao, S. Tuttas, L. Hoegner, and U. Stilla, “Unsupervised segmentation of point clouds from buildings using hierarchical
clustering based on gestalt principles,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, no. 99,
pp. 1–17, 2018.
[110] E. H. Lim and D. Suter, “3d terrestrial lidar classifications with super-voxels and multi-scale conditional random fields,” ComputerAided Design, vol. 41, no. 10, pp. 701–710, 2009.
[111] Z. Li, L. Zhang, X. Tong, B. Du, Y. Wang, L. Zhang, Z. Zhang, H. Liu, J. Mei, X. Xing, et al., “A three-step approach for tls point
cloud classification,” IEEE Transactions on Geoscience and Remote Sensing, vol. 54, no. 9, pp. 5412–5424, 2016.
[112] L. Wang, Y. Huang, Y. Hou, S. Zhang, and J. Shan, “Graph attention convolution for point cloud semantic segmentation,” in Proceedings
of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 10296–10305, 2019.
[113] J.-F. Lalonde, R. Unnikrishnan, N. Vandapel, and M. Hebert, “Scale selection for classification of point-sampled 3d surfaces,” in Fifth
International Conference on 3-D Digital Imaging and Modeling (3DIM’05), pp. 285–292, IEEE, 2005.