大家好,欢迎来到程序视点!我是小二哥。
在前面的文章中,我们解释过:计算机的底层只能处理二进制格式的数据,也就是0和1,其他的文字、数字、字符等信息都要转换成二进制的格式。之后,又在此基础上,介绍了八进制、十六进制,以及BCD码的转换问题。

大家会发现,我们所有的示例都是在整数的基础上处理的。那小数呢?
在现实生活中,小数可也是普遍存在的。那你有没有思考过,这些小数在计算机中是如何存储的呢?

刚才说过了,计算机只认0和1。要想让计算机认识小数,那就得把小数转为二进制形式。任何一个数,我们都可以看成这样格式:
整数部分+ 小数部分
比如,25就可以看成只有整数部分;0.125就看成只有小数部分;123.6875就是整数部分得 123 加上小数部分的 0.6875。我想任何一个数都应该可以这样划分。
对于整数部分,转为二进制时,我们采用除基取余法,具体的原理和过程之前文章讲解过。现在我们只需要把小数部分表示出来就好。
对于小数部分采用乘基取整法。ps:先不要问为什么?这个会在后面一两篇文章里讲清楚。本文重点是知道怎么用二进制表示小数。
我们那刚才例子种,又有整数,又有小数的123.6875来解析吧。先来整数部分的 123。还记得那个顺口溜吗?除2取余,逆排序
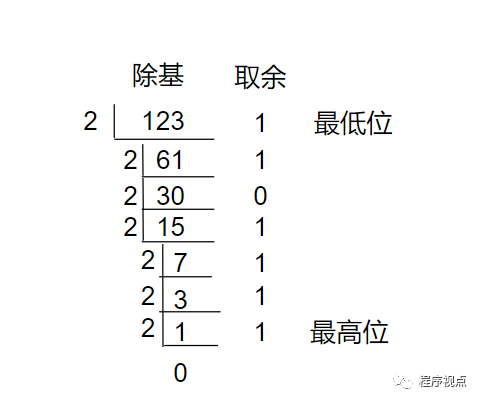
得到整数部分的二进制:1111011。
现在轮到小数部分的0.6875。采用乘基取整法:小数部分乘基取整,最先取得的整数为最高位,最后取得的整数位最低位,乘积为0时结束。
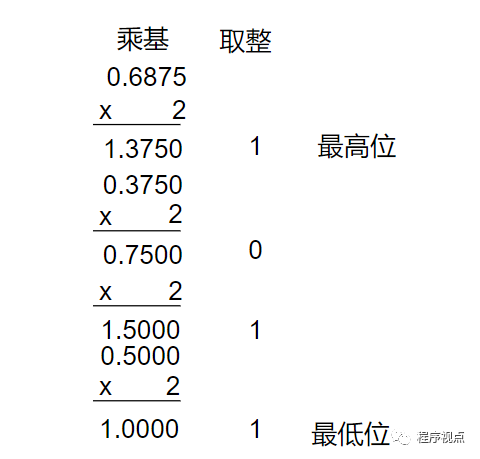
得到小数部分的二进制:1011。
把两个二进制拼起来是这样的:

假设我们用 32 个bit位来表示,那么最前面的那个0是符号位,中间还有些0(我就用省略号代替了),结尾部分就是上面红色代表的整数位和绿色代表的小数位。
在这个红色部分和绿色部分之间,应该有一个划分区间的标识,不然这和我们整数的0111 1011 1011就没区别了。十进制中,我们有小数点(.)进行划分。但计算机中并没有专门的部件对小数点(.)进行存储和处理的呀!
为了解决这个问题,计算机科学家们就开始想啦。“不就是想用几个bit位表示小数部分吗?那我们约定几个bit位是用来表示小数不就好了吗?” 于是,就约定某个固定的bit位就是小数点(.)的位置。这就是我们计算机知识中定点数的由来。
定点数的意思是:小数点的位置在计算机的存储是约定好的,固定的。比如上面的例子,我们就约定后4个bit位用来表示小数,前28个bit位表示整数,那计算机就知道怎么划分了,也就知道整数部分和小数部分分别是多少啦~
其他
关于计算机中小数的问题,还远远没完呐。想想上面说的定点数,它通过固定bit位的个数来约定小数部分。就拿刚才例子中约定的4个bit位来讲。4个bit位能表示多少个小数呢?必然是有限个小数的值呀!可我们的小数可不只是有限个呢?
呜~呜~要解决的问题还很多!好在计算机科学家们已经帮我们解决了这些问题了。我们下期接着聊吧~