(一)一个基本概念
分贝(dB):按照对数定义的一个幅度单位。对于电压值,dB以20log(VA/VB)给出;对于功率值,以10log(PA/PB)给出。dBc是相对于一个载波信号的dB值;dBm是相对于1mW的dB值。对于dBm而言,规格中的负载电阻必须是已知的(如:1mW提供给50Ω),以确定等效的电压或电流值。
(二)静态指标定义
1、量化误差(Quantization Error)
量化误差是基本误差,用简单3bit ADC来说明。输入电压被数字化,以8个离散电平来划分,分别由代码000b到111b去代表它们,每一代码跨越Vref/8的电压范围。代码大小一般被定义为一个最低有效位(Least Significant Bit,LSB)。若假定Vref=8V时,每个代码之间的电压变换就代表1V。换言之,产生指定代码的实际电压与代表该码的电压两者之间存在误差。一般来说,0.5LSB偏移加入到输入端便导致在理想过渡点上有正负0.5LSB的量化误差。
2、偏移与增益误差(Offset Gain Error)
器件理想输出与实际输出之差定义为偏移误差,所有数字代码都存在这种误差。在实际中,偏移误差会使传递函数或模拟输入电压与对应数值输出代码间存在一个固定的偏移。通常计算偏移误差方法是测量第一个数字代码转换或“零”转换的电压,并将它与理论零点电压相比较。增益误差是预估传递函数和实际斜率的差别,增益误差通常在模数转换器最末或最后一个传输代码转换点计算。
为了找到零点与最后一个转换代码点以计算偏移和增益误差,可以采用多种测量方式,最常用的两种是代码平均法和电压抖动法。代码平均测量就是不断增大器件的输入电压,然后检测转换输出结果。每次增大输入电压都会得到一些转换代码,用这些代码的和算出一个平均值,测量产生这些平均转换代码的输入电压,计算出器件偏移和增益。电压抖动法和代码平均法类似,不同的是它采用了一个动态反馈回路控制器件输入电压,根据转换代码和预期代码的差对输入电压进行增减调整,直到两代码之间的差值为零,当预期转换代码接近输入电压或在转换点附近变化时,测量所施加的“抖动”电压平均值,计算偏移和增益。
3、微分非线性(Differential nonlinearity,DNL)
见上一篇。
4、积分非线性(Integral nonlinearity,INL)
见上一篇。
(三)动态指标定义
1、有效位数(ENOB):模数转换器(ADC)与输入频率fIN相关的测试指标(位)。随着fIN的增大,整体噪声(特别是失真成分)将会增大,因而降低了ENOB和SINAD性能。另请参考:信号与噪声 + 失真比(SINAD)。ENOB与SINAD的关系式为:
注:位数和有效位数的区别
因为理想的ADC(只包含量化噪声)的信噪比可有公式:
SNR = (1.76 + 6.02*N)dB
计算得到,其中噪声只包含量化噪声。如果ADC没有其他噪声而只有量化噪声的话,则采样位数N和有效位数Neff一样。
但实际情况中还有一些其他噪声存在,所以通过上述公式计算出的位数N就是有效位数,它要小于N(采样位数),这里就有了采样位数和有效位数之分。
即采样位数N是只有量化误差时,ADC能够到达的处理精度;
有效位数Neff是实际处理中,ADC能够到达的处理精度。
2、分辨率:模拟信号被量化时,它是以有限的离散电压电平表示的,分辨率是用来表示信号的离散电平个数。为了更精确地恢复模拟信号,必须提高分辨率。分辨率通常定义为位数,利用更高的分辨率进行转换可以降低量化噪声。
3、均方根(RMS):表示交流信号的有效值或有效直流值。对于正弦波,RMS是峰值的0.707倍,或者是峰-峰值的0.354倍。
4、无杂散动态范围(SFDR):正弦波fIN (对于ADC指的是输入正弦波,对于ADC/DAC指的是重建的输出正弦波)的RMS值与在频域观察到的杂散信号的RMS值之比,典型值以分贝表示。SFDR在一些需要最大转换器动态范围的通信系统中非常重要。
无杂散动态范围表明模数转换器在输入大信号的同时所能检测到的最小信号的能力,这也是实际应用中的一个非常重要的性能参数。当转换器用在过采样率很高或者转换器的频谱性能很重要的情况下,无杂散动态范围的指标是标志系统性能的一个很重要的参数。
5、总谐波失真(THD):出现在输入(DAC为输出)频率整数倍频点(谐波)的失真的RMS值与输入(或输出)正弦波的RMS值之比。测量中仅包括奈奎斯特频限内的谐波,典型值以分贝表示:
式中,V2 至Vx是基波V1的谐波。
6、信号与噪声 + 失真比(SINAD):直流到奈奎斯特频段内,正弦波fIN (对于ADC指的是输入正弦波,对于ADC/DAC指的是重建的输出正弦波)的RMS值与转换器噪声的RMS值之比,包括谐波成分。典型值以分贝表示,另请参考关于均方根(RMS)和总谐波失真的注释。
7、dBFS(dB Full Scale) :是数字信号电平单位,简称满度相对电平。Full Scale 指0 dBFS 的位置, 0 dBFS就是最大编码电平,不同ADC的0 dBFS 实际对应值不同,它也是数字峰值表满度的参考电平。数字信号以ADC能处理的最大模拟信号的编码为最大值,即0 dBFS, 实际数字信号的幅度的编码相对于这个最大值的信号编码所代表的幅度之比,即为满度相对电平(dBFS)。因为规定最大值为0 的位置,所以,一片ADC实际处理的信号的满度相对电平都是负值。
一个12位的ADC芯片的dBFS的求法:
dBFS = 20 * log10(采样信号 / 1111 1111 1111)。
所以在ADC数据文档中经常看到fin = -1dBFS;这样通过上面公式可以计算得到,这里的-1dBFS的fin的幅度相当于满刻度输入幅度的0.8913。
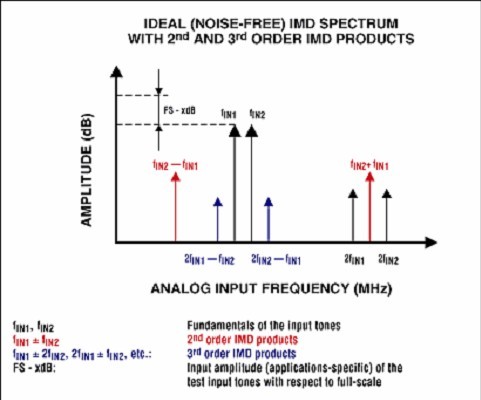
8、TWO-TONE IMD(two-tone intermodulation distortion):双阶互调失真
TWO-TONE IMD是ADC处理两个正弦波的混合信号时,在两个输入信号fin1 和 fin2 的(fin1 -fin2)和(fin1 +fin2)频点处产生的谐波失真。
如下图所示:
发布者:全栈程序员栈长,转载请注明出处:https://javaforall.cn/168054.html原文链接:https://javaforall.cn