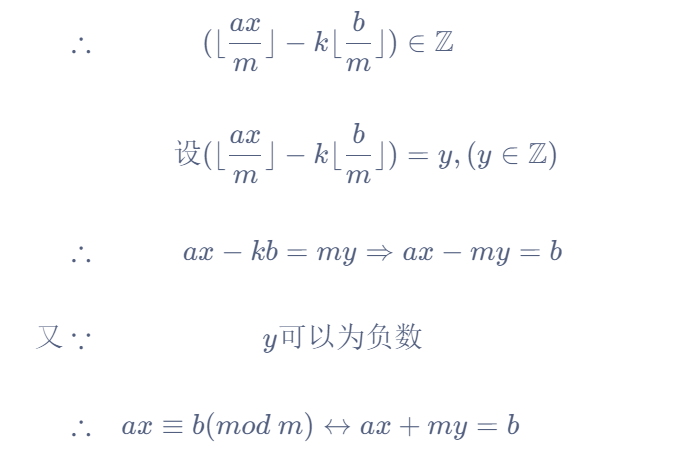1. 预习内容
1.1 阅读资料
- 欧几里得算法
- 裴蜀定理
- 同余定理
- 线性同余方程
1.2 练习题目
例题1 两个数的最大公约数
原题链接
描述
输入2个正整数a,b,求a与b的最大公约数。
输入
2个正整数a,b,中间用空格隔开。(1<=a,b <= 104)
输出
输出a与b的最大公约数。
样例输入
6 15样例输出
3代码 1
#include <bits/stdc++.h> using namespace std;int main(){
int a, b; cin >> a >> b; int flag = 1; for(int i = 2; i <= min(a,b); i++){ if(a % i == 0 && b % i == 0) flag = max(flag,i); } cout << flag << "\n"; return 0;
}
代码 2
#include <bits/stdc++.h>
using namespace std;int gcd(int a, int b){
return b ? gcd(b,a%b) : a;
}int main(){
int a, b; cin >> a >> b; cout << gcd(a,b) << "\n"; return 0;
}
2. 课程内容
2.1 数论简介
数学题在算法竞赛中经常出现,在竞赛中经常把数学模型和其他算法结合起来,出综合性的题目。
分类:
- 整除性问题:整除、最大公约数、最大公倍数;欧几里得算法、扩展欧几里得算法。
- 公式计算:高精度计算、概率和数学期望
- 素数问题:素数判定、筛法、区间素数统计。
- 同余问题:模运算、同余方程、快速幂、中国剩余定理、逆元、整数分解、同余定理、不定方程。
- 积性函数:欧拉函数、伪随机数、莫比乌斯反演。
- 多项式与生成函数:快速傅里叶变换、普通生成函数、指数生成函数。
- 递推关系:Fibonacci数列、Stirling数、Catalan数。
- 群论:Polya定理。
- 线性规划:单纯形法。
- 线性代数:矩阵、高斯消元。
- 博弈论:公平组合游戏、非公平组合游戏。
- 排列组合:容斥原理、抽屉原理、康托展开、排列生成、组合生成
特点
- 涉及大量数学定理、数学模型和公式计算,综合程度高
- 需要将题目抽象出其数学模型,或根据条件推理出规律进行求解
2.2 欧几里得算法
1. 简介与证明
概念
- 最大公约数指两个或多个整数共有约(因)数中最大的数
- 最小公倍数指两个或多个整数的公倍数里最小的数
- 欧几里得算法:又称辗转相除法,用于计算两个非负整数 a 和 b 的最大公约数
思想
- 辗转相除法求最大公约数 求100和18的最大公约数?
`$
\begin{aligned}
&1.令a_0=100,b_0=18\\
&\lfloor \frac{a_0}{b_0} \rfloor = 5,a_0-\lfloor \frac{a_0}{b_0} \rfloor\times b_0 = 10\\
&2.令a_1=b_0=18,b_1=a_0~mod~b_0=10\\
&\lfloor \frac{a_1}{b_1} \rfloor = 1,a_1-\lfloor \frac{a_1}{b_1} \rfloor\times b_1 = 8\\
&3.令a_2=b_1=10,b_2=a_1~mod~b_1=8\\
&\lfloor \frac{a_2}{b_2} \rfloor = 1,a_2-\lfloor \frac{a_2}{b_2} \rfloor\times b_2 = 2\\
&4.令a_3=b_2=8,b_3=a_2~mod~b_2=2\\
&\lfloor \frac{a_3}{b_3} \rfloor = 0,a_3-\lfloor \frac{a_3}{b_3} \rfloor\times b_3 = 4\\
&即最大公约数为b_3=2
\end{aligned}
$`
求 100 和18 两个正整数的最大公约数,用欧几里得算法,是这样进行的:
100 / 18 = 5 (余 10) 100%8=10
18 / 10= 1(余8) 18%10=8
10 / 8 = 1(余2) 10%8=2
8 / 2 = 4 (余0) 8%2=0
至此,最大公约数为2
以除数和余数反复做除法运算,当余数为 0 时,取当前算式除数为最大公约数,所以就得出了 100 和 18 的最大公约数2。
- 求N 和M 的最小公倍数lcm(N,M) ,则先求N 和M 的最大公约数gcd(N,M) ,然后\frac{N\times M}{gcd(N,M)} 则为最小公倍数。
2. 算法模板
//最大公约数 int gcd(int a, int b){ return b ? gcd(b, a % b) : a; }
//最小公倍数
int lcm(int a,int b){
return a / gcd(a,b) * b;
}
3. 最大公约数
原题链接
描述
输入两个正整数a、b,求a、b的最大公约数。要求采用递归函数实现。
输入
输入两个正整数a、b。
输出
输出a、b的最大公约数。
20 15样例输出
样例输出
5代码
#include <bits/stdc++.h>
using namespace std;int gcd(int a, int b){
return b ? gcd(b,a % b) : a;
}int main(){
int a, b; cin >> a >> b; cout << gcd(a,b) << "\n"; return 0;
}
4. 多个数的最小公倍数
原题链接
题目描述
输入n个数,请计算它们的最小公倍数。如5、7、15的最小公倍数是105。
输入
首先输入一个正整数T,表示测试数据的组数,然后是T组的测试数据。
每组测试先输入一个整数n(2<=n<=20),再输入n个正整数(n属于1,100000),这里保证最终的结果在int型范围内。
输出
对于每组测试,输出n个整数的最小公倍数。
样例输入
2
3 5 7 15
5 1 2 4 3 5样例输出
105
60分析
- 求多个数的最小公倍数,可以两两相求
代码
#include <bits/stdc++.h>
using namespace std;int gcd(int a,int b){
return b ? gcd(b,a % b) : a;
}int lcm(int a,int b){
return a / gcd(a,b) * b;
}void solve(){
int n; cin >> n; int t; cin >> t; for(int i = 2; i <= n ; i++){ int x; cin >> x; t = lcm(t,x); if(i == n) cout << t << '\n'; }}
int main(){
int _; cin >> _; while(_--){ solve(); } return 0;
}
2.3 扩展欧几里得算法
1. 简介与证明
作用
- 求形如ax+by=gcd(a,b) 的方程的解x,y
思想
- 欧几里得算法:gcd(a,b)=gcd(b,a%b) ,特别的gcd(a,0)=a
- 裴蜀定理:对于任意正整数a,b ,一定存在非零的x,y ,使得ax+by=gcd(a,b)
$</p></blockquote><p> \begin{cases}</p><p> b=0时:\begin{cases}</p><p> gcd(a,b)=a\ax+by=gcd(a,b)\</p><p> \end{cases}\Rightarrow\begin{cases}x=1\y=0\end{cases}</p><p> \</p><p> \</p><p> \</p><p> \</p><p> \</p><p> b\neq0时:</p><p> \begin{cases}</p><p> \begin{aligned}</p><p> ①&设~ax+by=gcd(a,b)=d\\</p><p> &\because 由欧几里得算法可知:gcd(a,b)=gcd(b,a\%b)=d\\</p><p> &\therefore 由裴蜀定理得:b{x}'+(a\%b){y}'=d\\</p><p> 又&\because ax+by=d\\</p><p> &\therefore联立</p><p> \begin{cases}</p><p> ax+by=d\b{x}'+(a\%b){y}'=d\a\%b=a-\lfloor\frac{a}{b}\rfloor b</p><p> \end{cases}\Rightarrow\begin{cases}x={y}'\y={x}'-\lfloor\frac{a}{b}\rfloor{y}'\end{cases}\\</p><p> ②&设{a}'=b,{b}'=a\%b\\</p><p> &\therefore gcd(b,a\%b)=gcd({a}',{b}')=d\\</p><p> &\because gcd({a}',{b}')=gcd({b}',{a}'\%{b}')=d\\</p><p> &\therefore {b}'{x}''+{a}'\%{b}'{y}''=d\\</p><p> 又&\because b{x}'+(a\%b){y}'=d\\</p><p> &\therefore联立\begin{cases}</p><p> b{x}'+(a\%b){y}'=d\{b}'{x}''+{a}'\%{b}'{y}''=d\{a}'\%{b}'={a}'-\lfloor\frac{{a}'}{{b}'}\rfloor{b}'</p><p> \end{cases}\Rightarrow\begin{cases}{x}'={y}''\{y}'={x}''-\lfloor\frac{{a}'}{{b}'}\rfloor{y}''</p><p> \end{cases}\\</p><p> ③&设{a}''={b}',{b}''={a}'\%{b}'\\</p><p> &\dots\</p><p> &\dots\</p><p> &直到b=0时,联立解得\begin{cases}{x}^i=1\{y}^i=0\end{cases}\\</p><p> &然后逐步返回每一次联立所得的结果\begin{cases}{x}^{i-1}={y}^{i}\{y}^{i-1}={x}^{i}-\lfloor\frac{{a}^{i}}{{b}^i}\rfloor{y}^{i}</p><p> &最后返回得到x和y的值</p><p> \end{cases}\</p><p> \end{aligned}</p><p> \end{cases}</p><p> \end{cases}</p><p> $注意
- 当方程符合ax+by=gcd(a,b) 的形式时,才可以用扩展欧几里得算法求解(x_0,y_0)
- 推论:可以进一步求解任意方程ax+by=n ,得到一个整数解
$</p></blockquote><p> \begin{aligned}</p><p> \begin{cases}</p><p> &(1)~~判断方程ax+by=n是否有整数解,有解的条件为:gcd(a,b)可以整除n\\</p><p> &(2)~~用扩展欧几里得算法求ax+by=gcd(a,b)得到一个解(x_0,y_0)\\</p><p> &(3)~~在ax_0+by_0=gcd(a,b)两边同时乘\frac{n}{gcd(a,b)}\Rightarrow\frac{ax_0n}{gcd(a,b)}+\frac{by_0n}{gcd(a,b)}=n\\</p><p> &(4)~~对照ax+by=n可知该方程的一个解为({x}',{y}'),其中\begin{cases}{x}'=\frac{x_0n}{gcd(a,b)}\\{y}'=\frac{y_0n}{gcd(a,b)} \end{cases}</p><p> \end{cases}</p><p> \end{aligned}</p><p> $2. 算法模板
void exgcd(int a, int b, int &x, int &y){if(!b){ //若b=0时 x = 1,y = 0; return ; } else{ //b!=0时 exgcd(b, a % b, x, y); //递归到下一层 int t = x; //返回时执行 x = y; y = t - a / b * y; }
}3. 解ax+by=gcd(a,b)方程
原题链接
描述
给定n 对正整数 a_i,b_i ,对于每对数,求出一组 x_i,y_i ,使其满足 a_i×x_i+b_i×y_i=gcd(a_i,b_i) 。
输入格式 第一行包含整数 n 。
接下来 n 行,每行包含两个整数 a_i,b_i 。
输出格式 输出共 n 行,对于每组a_i,b_i ,求出一组满足条件的 x_i,y_i ,每组结果占一行。
本题答案不唯一,输出任意满足条件的 x_i,y_i 均可。
数据范围 1≤n≤105, 1≤a_i,b_i≤2×10^9 输入样例:
代码语言:javascript复制2
4 6
8 18输出样例:
代码语言:javascript复制-1 1
-2 1代码
代码语言:javascript复制#include <bits/stdc++.h>
using namespace std;void exgcd(int a,int b,int &x,int &y){
if(!b){x=1,y=0; return ;} else{ exgcd(b,a%b,x,y); int t=x; x=y; y=t-a/b*y; }}
int main(){
int n; cin>>n; while(n--){ int a,b,x,y; cin>>a>>b; exgcd(a,b,x,y); cout<<x<<" "<<y<<endl; } return 0;
}4. 解一元线性同余方程
概念
- ax\equiv b(mod
m),即\frac{ax}{m} 与\frac{b}{m} 的余数相同,且a,b,m 为整数,求x 的值- 该方程即为一元线性同余方程
思想
- 对ax\equiv b(modm) 做等价变形:ax+my=b
$</p></blockquote><p> $
- 由扩展欧几里得算法的推论可知:当且仅当 gcd(a,m) 可以整除b 时,ax+my=b 存在整数解
$</p></blockquote><p> 由扩展欧几里得算法可知:</p><p> \begin{cases}</p><p> 当gcd(a,m)=b时:\begin{cases}x=x_0\y=y_0\end{cases}\\</p><p> 当gcd(a,m)为b的整数倍时:\begin{cases}{x}'=\frac{x_0b}{gcd(a,m)}\{y}'=\frac{y_0b}{gcd(a,m)}\end{cases}</p><p> \end{cases}</p><p> $例题 878. 线性同余方程
原题链接
描述
给定 n 组数据 a_i,b_i,m_i ,对于每组数求出一个 x_i ,使其满足 a_i×x_i≡b_i(mod~m_i) ,如果无解则输出 impossible。
输入格式 第一行包含整数 n 。
接下来 n 行,每行包含一组数据 a_i,b_i,m_i 。
输出格式 输出共 n 行,每组数据输出一个整数表示一个满足条件的 x_i ,如果无解则输出 impossible。
每组数据结果占一行,结果可能不唯一,输出任意一个满足条件的结果均可。
输出答案必须在
int范围之内。数据范围 1≤n≤105 , 1≤a_i,b_i,m_i≤2×10^9
代码语言:javascript复制2
2 3 6
4 3 5输出样例:
输出样例:
代码语言:javascript复制impossible
-3代码
代码语言:javascript复制#include <bits/stdc++.h>
using namespace std;typedef long long LL;
LL gcd(LL a,LL b){
return b ? gcd(b,a % b) : a;
}void exgcd(LL a,LL b,LL &x,LL &y){
if(!b){ //若b=0时 x=1,y=0; return ; } else{ exgcd(b,a%b,x,y); LL t=x; x=y; y=t-a/b*y; }}
int main(){
int n; cin>>n; while(n--){ LL a,b,m,x,y; cin>>a>>b>>m; LL d=gcd(a,m); exgcd(a,m,x,y); if(b%d) cout<<"impossible"<<endl; else cout<<b/d*x%m<<endl; } return 0;
}3. 推荐阅读
- OI WIKI
- 基础数学初识