【导读】专知成员Hui上一次为大家介绍Numpy包的使用,介绍了Numpy库的一些基本函数和一些简单用法,以及图像灰度变换,这一次为大家详细讲解图像的缩放、图像均匀操作和直方图均衡化。

图像的缩放、均匀操作和直方图均衡化
上一讲我们已经介绍了Numpy库的一些基本函数和一些简单的用法,这一讲我们将继续学习使用Numpy库对图像进行更深入且更加有趣的操作。
▌图像的缩放
Numpy的数组对象是我们处理图像和数据的主要工具。想要对图像进行缩放处理没有现成的简单的方法。因此我们使用如下代码实现图像的缩放:
from PIL import Image from numpy import * from pylab import *def imresize(im, sz):
pil_im = Image.fromarray(uint8(im))
return array(pil_im.resize(sz))im = Image.open("test.jpg")
im1 = imresize(im, (128, 128))figure()
gray()subplot(1, 2, 1)
imshow(im)subplot(1, 2, 2)
imshow(im1)
title("Zoom picture")
show()
输出的结果如下图所示:

这其中,我们定义了一个imresize()函数,使用PIL对象重新定义图像数组的大小,其中,fromarray()方法进行反相操作,uint8:将其他数据类型转换为uint8
▌图像均匀
图像均匀操作是减少图像噪声的一种简单方式,通常用于艺术特效,我们可以简单的从图像列表中计算出一幅平均图像,假设所有的图像具有相同的大小,我们可以将这些图像简单的相加,然后除以图像的数目,来计算平均图像,下面的函数可以用来计算平均图像:
def compute_average(imlist):
averageim = array(Image.open(imlist[0]), 'f')
for imname in imlist[1:]:
try:
averageim += array(Image.open(imname))
except:
print(imname + '...skipped')
averageim /= len(imlist)
return array(averageim, 'unit8')这个函数中包含了一些基本的异常处理技巧,可以自动跳过不能打开的图像,我们还可以使用mean()函数计算平均图像。mean()函数需要将所有的图像堆积到一个数组中;也就是说,如果有很多幅图像,该处理方式会占用大量内存。
完整的代码为:
from PIL import Image
import numpy as np
from pylab import *
import matplotlib.pyplot as plt
import os
def compute_average(imlist):
"""计算图像列表的平均像素"""
# 打开第一幅图像,将其存储在浮点型数组中
averageim = array(Image.open(imlist[0]), 'f')
for imname in imlist[1:]:
try:
averageim += array(Image.open(imname))
except:
print
imname + "...skipped"
averageim /= len(imlist)
return array(averageim, 'uint8')
if name == "main":
dirs = os.listdir("/home/xuna/桌面/image")
imlist = []
for name in dirs:
name = "/home/xuna/桌面/image/" + name
imlist.append(name)
print
imlist
im = compute_average(imlist)
imshow(im)
show()▌直方图均衡化
图像灰度变换中有一个非常有用的例子就是直方图均衡化。由之前的灰度图像的直方图可以看出,一般情况下,图像上某些灰度值较多,有些灰度值较少,直方图均衡化为的是使灰度值较为均衡。那么为什么要进行图像均衡化呢?是因为均衡化的图像能够提高对比度和灰度色调的变化,使图像更加清晰。均衡化的图像意味着它的像素占有很多的灰度级而且分布均匀,它往往有高对比度和多变的灰度色调。
从图片本身的角度看,直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同,把给定图像的直方图分布改变成“均匀”分布直方图分布。
那么如何进行图像均衡化呢?对于任意一副灰度分布不均匀的图像,为了使图像直方图信息自动达到均匀分布,我们需要引入一个变换函数。这个变换函数的基本思想是对图像中像素个数多的灰度级进行展宽,而对图像中像素个数少的灰度进行压缩,即将一幅图像的灰度直方图变平,使变换后的图像中每个灰度值的分布概率都相同从而扩展像元取值的动态范围。
这个变换函数通常是图像中像素值的累积分布函数(cumulativate distribution function,简写为cdf,将像素值的范围映射到目标范围的归一化操作),累积函数和概率论中的累积分布函数类似。例如对于还有5个数的序列[1,2,3,4,5],其累积函数含有5个数,第一个数是1,第二个是1+2=3,……,第五个数是1+2+3+4+5=15,所以其累积函数是[1,3,6,10,15]。需要注意的是,不论像素无论怎么映射,一定要保证原来的大小关系不变,较亮的区域,依旧是较亮的,较暗依旧暗,只是对比度增大,绝对不能明暗颠倒。
直方图变换其实是一种灰度变换,灰度变换的变换函数决定了输入随机变量与输出随机变量之间的关系,也就是两个随机变量的关系;一副图像是二维离散的数据,不利于使用数学的工具进行处理,在数字图像处理中,我们通常是采用连续的变量进行推导,最后在推广到离散的情况。
在对图像做进一步处理之前,直方图均衡化通常是对图像灰度值进行归一化的一个非常好的方法,并且可以增强图像的对比度。
我们用r和s分别表示原图像灰度级和经直方图均衡化之后的图像灰度级,为了方便我们讨论,我们首先要做的事便是对s和r的归一化处理,使得:
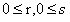
对于一幅给定的图像,归一化之后灰度级分布在范围内。对[0,1]区间内任一个r至进行如下变换:
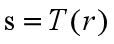
我们令从s到r的反变换为:
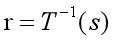
r的概率密度为P_{r}(r) ,s的概率密度为:
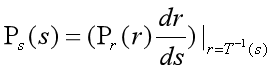
我们令变换函数为:
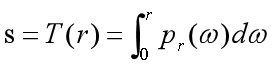
该函数就称为r的累积分布函数,对式中r求导有:
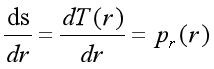
把结果带入前式:

由此可见,变换后变量s在其定义域内的概率密度是均匀分布的,用r的累积分布函数做变换函数,可以产生一幅灰度级分布具有均匀概率密度的图像,这个结果扩展了像素取值的动态范围。
我们把直方图均衡化的过程封装在一个函数里面,函数名字叫做histeq,输入原图像矩阵和直方图分块数,输出均衡化后的图像矩阵和累积函数。
具体的代码如下:
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
import matplotlib.cm as cmdef histeq(image_array, image_bins=256):
# 将图像矩阵转化成直方图数据,返回元组(频数,直方图区间坐标)
image_array2, bins = np.histogram(image_array.flatten(), image_bins)
# 计算直方图的累积函数
cdf = image_array2.cumsum()
# 将累积函数转化到区间[0,255]
cdf = (255.0 / cdf[-1]) * cdf
# 原图像矩阵利用累积函数进行转化,插值过程
image2_array = np.interp(image_array.flatten(), bins[:-1], cdf)
# 返回均衡化后的图像矩阵和累积函数
return image2_array.reshape(image_array.shape), cdf
image = Image.open("test.jpg").convert("L")
image_array = np.array(image)fig = plt.figure(figsize=(15, 15))
ax = fig.add_subplot(2, 2, 1)
ax.hist(image_array.flatten(), 256)
plt.subplot(2, 2, 2)
plt.imshow(image_array, cmap=cm.gray)
plt.axis("off")a = histeq(image_array) # 利用刚定义的直方图均衡化函数对图像进行均衡化处理
plt.subplot(2, 2, 3)
plt.hist(a[0].flatten(), 256)
plt.subplot(2, 2, 4)
plt.imshow(Image.fromarray(a[0]), cmap=cm.gray)
plt.axis("off")
plt.show()
输出结果为:
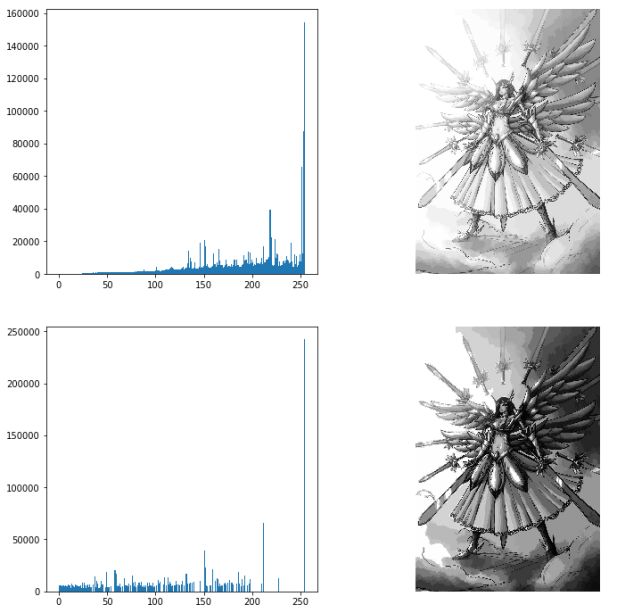
比较上面输出的均衡化之前和均衡化之后的两幅直方图,我们可以清晰的看出直方图均衡化后的图像对比度增强了,原先图像灰色区域的细节变得更加清晰。
参考文献:
python计算机视觉编程:http://yongyuan.name/pcvwithpython/