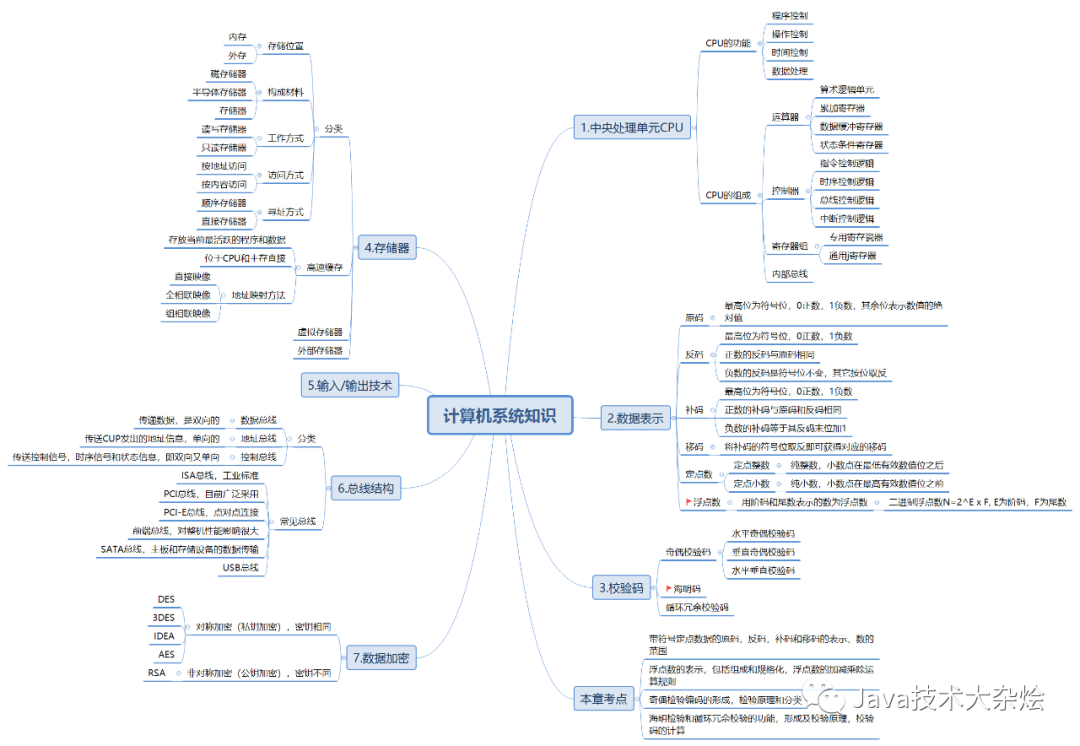
该篇主要介绍计算机系统的基础知识,体系结构,安全性,可靠性和系统性能测评等。下图是该篇的一个思维导图:
原码
原码的定义如下:数值X的原码记为
[X]_{原},如果机器字长为n(即n个二进制位表示),则原码的定义如下:
- 若X是纯整数:
[X]_{原}= \begin{cases} X, & \text 0 \leq X \leq 2^{n-1} - 1 \\ 2^{n-1} + |X| & \text -2^{n-1} \leq X \leq 0 \end{cases}
- 若X是纯小数:
[X]_{原}= \begin{cases} X & \text 0 \leq X < 1 \\ 2^{0} + |X| & \text -1 < X \leq 0 \end{cases}
在原码表示法中,最高位是符号位,0为正数,1为负数,其余的n-1位表示数值的绝对值。
0的原码有两种表现形式:
[+0_{原}] = 00000000
[-0_{原}] = 10000000
反码
反码的定义如下:数值X的反码记为
[X]_{反},如果机器字长为n,则反码的定义如下:
- 若X是纯整数:
[X]_{反}= \begin{cases} X, & \text 0 \leq X \leq 2^{n-1} - 1 \\ 2^{n-1} + X & \text -(2^{n-1}-1) \leq X \leq 0 \end{cases}
- 若X是纯小数:
[X]_{反}= \begin{cases} X & \text 0 \leq X < 1 \\ 2- 2^{-(n-1)} + X & \text -1 < X \leq 0 \end{cases}
在反码表示法中,最高位是符号位,0为正数,1为负数。
- 正数的反码与原码相同。
- 负数的反码等于其原码的基础上, 符号位不变,其余各位取反.
0的反码有两种表现形式:
[+0_{反}] = 00000000
[-0_{反}] = 11111111
补码
补码的定义如下:数值X的补码记为
[X]_{补},如果机器字长为n,则补码的定义如下:
- 若X是纯整数:
[X]_{补}= \begin{cases} X, & \text 0 \leq X \leq 2^{n-1} - 1 \\ 2^{n} + X & \text -2^{n-1} \leq X \leq 0 \end{cases}
- 若X是纯小数:
[X]_{补}= \begin{cases} X & \text 0 \leq X < 1 \\ 2 + X & \text -1 \leq X < 0 \end{cases}
在补码表示法中,最高位是符号位,0为正数,1为负数。
- 正数的补码与原码,反码相同
- 负数的补码等其反码末尾加1
在补码中,0有唯一的编码:
[+0_{补}] = [-0_{补}] = 00000000
移码
移码表示码是在数X上增加一个偏移量来定义的,常用于表示浮点数中的阶码。
如果机字长为n,规定偏移量为
2^{n-1},则移码的定义如下:
- 若X是纯整数:
[X_{移}] = 2^{n-1} + X(-2^{n-1} \leq X < 2^{n-1})
- 若X是纯小数:
[X_{移}] =1 + X(-1 \leq < 1)
各种码制表示的数值范围
浮点数
浮点数所能表示的数值范围由阶码决定,精度由尾数决定。
需要掌握浮点数的运算