广义线性模型应用举例之泊松回归及R计算
在前文“广义线性模型”中,提到广义线性模型(GLM)可概括为服务于一组来自指数分布族的响应变量的模型框架,正态分布、指数分布、伽马分布、卡方分布、贝塔分布、伯努利分布、二项分布、负二项分布、多项分布、泊松分布、集合分布等都属于指数分布族,并通过极大似然估计获得模型参数。
本篇继续简介广义线性模型的常见子类,泊松回归(poisson regression)。泊松回归假设响应变量服从泊松分布、方差和均值相等,并且假设各组自变量独立(多元回归情形)。当期望通过给定的自变量预测或解释计数型结果变量时,泊松回归是一个非常有用的工具。
生物学数据中很多都是计数型数值,通常具有这些特点:(1)数值是离散的,并且只能是非负整数;(2)数值分布倾向于在特定较小范围内聚集,并具有正偏态的分布特征;(3)通常会出现很多零值;(4)方差随均值而增加。
某些计数型变量可以通过正态分布进行近似,并可以使用一般线性回归进行合理建模。但更普遍做法是使用广义线性模型,如泊松回归或负二项回归,它们都是应用于计数型(非负整数)响应变量的回归模型。泊松或负二项分布都是离散的概率分布,具有两个重要的属性:(1)数值仅包含非负整数;(2)方差是均值的函数。在早期,计数数型变量常通过数据变换或通过非参数假设检验进行分析,现如今更普遍使用广义线性模型方法的主要原因是可以获得可解释的参数估计。
关于负二项回归在前文“负二项回归”中已作过简介。下文则主要以一个简单示例,展示泊松回归在R语言中的计算过程,及对结果的解读。
R语言执行泊松回归的简单示例
节选了马里兰州河流生物资源调查(https://dnr.maryland.gov/streams/Pages/mbss.aspx)的部分数据,一个生物学目的是探索可能影响鱼类物种丰度的环境因素,并对物种丰度变化的原因作出解释。
下文的测试数据,R代码等的百度盘链接(提取码,60w9):
https://pan.baidu.com/s/1Js7kO5R3uL_u6-67mkv3_A
若百度盘失效,也可在GitHub的备份中获取:
https://github.com/lyao222lll/sheng-xin-xiao-bai-yu
示例数据概要
就节选的部分数据为例,记录了所调查的马里兰州河流中每75米长的区段水域内,鱼类物种Rhinichthys cataractae的丰度,并测量了每段水域中相应的环境特征。

其中第一列代表了调查河流区段的位置信息,其余各列依次为:
fish,水域中R. cataractae的个体数量,代表了物种丰度,一组计数型变量;
acre,水域流域面积(英亩,acre);
do2,水域溶解氧含量(毫克/升,mg/L);
depth,水域最大深度(厘米,cm);
no3,水域硝酸盐浓度(毫克/升,mg/L);
so4,水域硫酸盐浓度(毫克/升,mg/L);
temp,水域温度(摄氏度,℃)。
探索性分析
分析目的是确定影响R. cataractae丰度的环境成因,R. cataractae丰度在分析中将作为响应变量,环境因子作为自变量对待。考虑到R. cataractae丰度是一组计数型变量,由离散型的非负整数组成(非连续型变量,比较特殊),不妨首先观测一下R. cataractae丰度变量的分布特征。
#读取鱼类物种丰度和水体环境数据 dat <- read.delim('fish_data.txt', sep = '\t', row.names = 1)#查看物种丰度变量的分布
library(ggplot2)ggplot(dat, aes(x = fish)) +
geom_histogram(bins = 30, fill = 'gray', color = 'black')
ggplot(dat, aes(x = fish, stat(density))) +
geom_histogram(bins = 30, fill = 'gray', color = 'black') +
geom_line(color = 'red', stat = 'density')
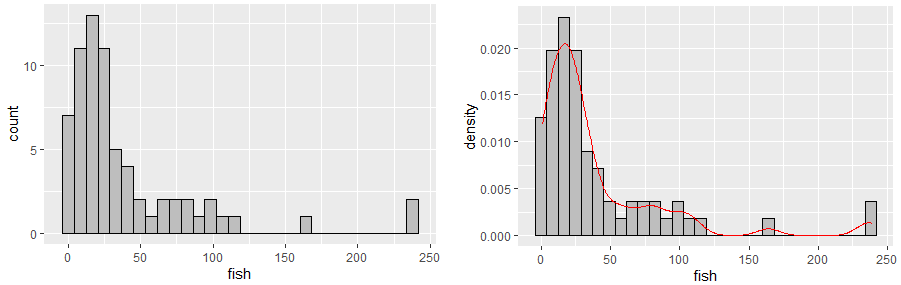
显示R. cataractae丰度变量分布右偏。再结合R. cataractae丰度是一组计数型变量,大致可以初步认为该物种丰度呈现泊松分布。
因此,对于后续分析R. cataractae丰度的环境因子关系的回归模型选择,就可以初步考虑广义线性模型中的泊松回归实现。
执行泊松回归及对模型解释
其实,该数据在前文“多元线性回归”中也曾作为示例演示过。前文在使用一般线性模型探索可能影响R. cataractae丰度的环境因素的过程中,最后发现acre(流域面积)、depth(水域深度)和no3(硝酸盐浓度)的增加有助于R. cataractae丰度的提升,即R. cataractae丰度与这3个环境变量之间存在一种线性增长响应。
先前考虑使用一般线性模型(多元线性回归)进行分析,仅仅是出于该方法最为简单直观,使得在大多数实际分析中经常将问题直接简化为一般线性模型去解释,并放松对正态性的假设。但是相对而言,当响应变量严重偏离正态分布时,一般线性模型可能就不尽如人意。在这个示例数据中,观察到响应变量R. cataractae丰度分布右偏而大致呈现泊松分布,提示使用泊松回归(广义线性模型)可能比线性回归(一般线性模型)更有效。
为了确认这一点,接下来就使用泊松回归实现对R. cataractae丰度和环境因子关系的建模。
如前文“广义线性模型概述”中提到,R语言中拟合广义线性模型的函数有很多,各自的特点也不同(大多是对基础功能的拓展,如包括考虑时间序列的模型,用于0时较多时的零膨胀模型,当数据存在离群点和强影响点时有用的稳健模型等),实际使用时参考文献中的方法描述以及自己数据集的特点进行选择即可。本示例直接使用基础包函数glm()作简单展示。
首先不妨使用全部环境变量拟合与R. cataractae丰度的多元泊松回归,本次计算过程中暂且忽略离群值以及多重共线性等的影响。
#拟合广义线性模型,详情 ?glm,这里通过 family 参数指定了泊松回归
fit_poisson <- glm(fish~acre+do2+depth+no3+so4+temp, data = dat, family = 'poisson')
summary.glm(fit_poisson) #展示拟合回归的简单统计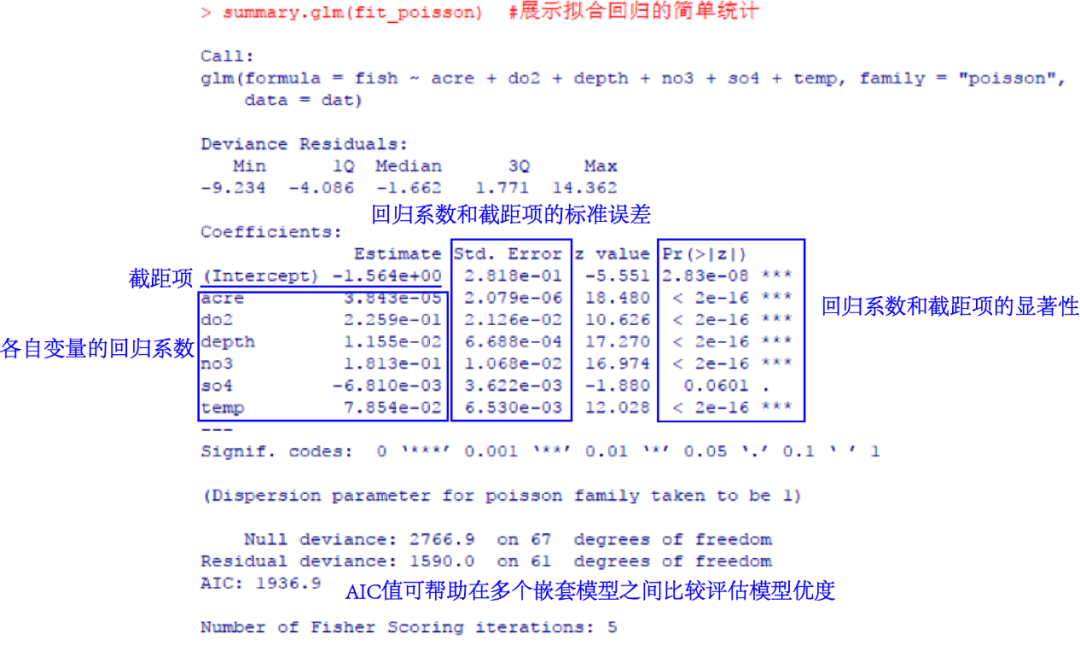
输出结果列出了回归系数、标准误和参数为0的检验。
首先根据检验的p值,可看到除了so4(水域硫酸盐浓度)外,其它自变量的水平都非常显著,表明acre(流域面积)、do2(水域溶解氧含量)、depth(水域深度)、no3(硝酸盐浓度)以及temp(水域温度)均是影响R. cataractae丰度的因素。尽管如此,so4也很接近显著水平了。
显著的正回归系数代表了当该环境变量的水平增加时,促进R. cataractae丰度提升;显著的负回归系数则表示该环境变量的水平增加时,R. cataractae丰度降低。在泊松回归中,响应变量以条件均值的对数形式loge(λ)来建模。在忽略该回归模型精度的前提下,对于各自变量的回归系数的意义这样解释:例如no3(硝酸盐浓度,mg/L)的回归系数0.1813,代表了在当其它自变量不变的情况下,硝酸盐浓度每升高1 mg/L时,R. cataractae丰度的对数均值将相应增加0.1813。截距项代表了当所有自变量都为0时,R. cataractae丰度的对数均值,但由于都为0的可能性极小(此时河流完全枯竭),因此截距项的意义不是很大。
通常在响应变量的初始尺度上解释回归系数比较容易。对于上述泊松回归统计结果,可以对各自变量的回归系数作个指数转换:
poisson_coef <- coef(fit_poisson) #提取回归系数
exp(poisson_coef) #指数化回归系数
泊松回归中,正值的回归系数将转化为>1的值,负值的回归系数将转化为<1的值。此时,在忽略该回归模型精度的前提下,对于no3(硝酸盐浓度,mg/L)的回归系数的指数转化值1.199,代表了在当其它自变量不变的情况下,硝酸盐浓度每升高1 mg/L时,期望的R. cataractae丰度将乘以1.199。
偏大离差及准泊松回归
总的来说,上述泊松回归显示了acre(流域面积)、do2(水域溶解氧含量)、depth(水域深度)、no3(硝酸盐浓度)以及temp(水域温度)均是显著影响R. cataractae丰度的因素,so4(水域硫酸盐浓度)虽不显著但也是临界水平。
但是在前文“多元线性回归”中使用同样数据的线性回归结果中,仅显示了acre(流域面积)、depth(水域深度)和no3(硝酸盐浓度)的增加有助于R. cataractae丰度的提升,即R. cataractae丰度与这3个环境变量之间存在一种线性增长响应。
前后两个不同模型(分别为线性回归和泊松回归)的结果比较,区别是非常明显的。那么,哪个结果更合理一些?上文虽然观察到了响应变量R. cataractae丰度的分布更趋于泊松分布,并提到当响应变量严重偏离正态分布时,线性回归可能差强人意,这样来看貌似泊松分布的结果更合理,真是如此吗?然而泊松回归常伴随偏大离差的问题,也是不可忽视的,甚至会带来非常糟糕的误解。
偏大离差及评估
在线性回归中,常通过检查残差来评价模型,一个正态响应模型的残差分布的均值应该为0,标准差为常数。泊松分布的方差和均值是相等的。由于拟合出的值是泊松分布均值的估计值,泊松回归的残差的方差应该与均值的预测值相等。因此,在对残差和拟合值作图时,随着均值预测值的增加,残差方差应该以相同的速度增加。对计数型变量进行泊松回归时,常遇到的问题是方差增加的速度比均值预测值增加的速度要快。即当响应变量观测的方差比依据泊松分布预测的方差大时,泊松回归可能发生偏大离差(overdispersion)。
处理计数型数据时经常发生偏大离差,会对结果的可解释性造成负面影响。例如,偏大离差的存在可能会得到很小的标准误和置信区间,使显著性检验过于宽松,产生II类错误(II类错误,接受并不真实存在的效应),导致潜在的误导性结论。
qcc包提供了一个对泊松模型偏大离差的检验方法。零假设不存在偏大离差,若检验p值显著,则拒绝零假设,偏大离差存在。
library(qcc)
qcc.overdispersion.test(dat$fish, type = 'poisson')

显示p<0.05,表明计数型变量R. cataractae丰度确实存在偏大离差。也就是说,上述的泊松回归结果可能并不可靠,甚至比先前通过线性回归所得结论还不稳定。这样一来,就不能盲目下结论谁更加合理。
幸运的是,目前已有许多对泊松回归的改进方案,以解决偏大离差问题。
准泊松回归(偏大离差的泊松回归)
存在偏大离差的计数型数据可以用考虑了偏大离差问题的泊松模型来拟合,也就是准泊松回归(也常称为偏大离差的泊松回归)。准泊松回归基于准泊松(quasi-poisson)分布,计数型变量的分布与泊松分布的均值相同,但方差是均值的w倍。因此所得到的具有偏大离差的泊松回归模型有相同的回归系数估计值,但回归系数的标准误会大很多,可以减少偏大离差的影响。
R函数glm()中,可以通过指定参数family='quasipoisson'(准泊松回归)代替先前的family='poisson'(泊松回归)。
#使用全部环境变量拟合与鱼类物种丰度的多元准泊松回归
#拟合广义线性模型,详情 ?glm,这里通过 family 参数指定了准泊松回归
#其余参数项使用默认值,和先前的泊松回归保持相同
fit_quasipoisson <- glm(fish~acre+do2+depth+no3+so4+temp, data = dat, family = 'quasipoisson')
summary.glm(fit_quasipoisson) #展示拟合回归的简单统计
#若和先前泊松回归结果做个比较,准泊松回归和泊松回归的唯一区别在回归系数标准误的估计值上

输出结果列出了回归系数、标准误和参数为0的检验,准泊松回归和泊松回归的唯一区别在回归系数标准误的估计值上。
能够看到,各自变量在准泊松回归中的回归系数和先前泊松回归的相比,没有改变。因此对于这里的回归系数的解读方式,和上文泊松回归是完全一致的,详见上文内容即可。
但回归系数的标准误变大了,此举扩大了标准误和置信区间,增加了显著性检验的严格度。也很容易注意到这里的p值也远比先前泊松回归中的大,因而会降低由偏大离差而可能导致的II类错误(II类错误,接受并不真实存在的效应)。
总的来说,观察到acre(流域面积)、depth(水域深度)、no3(硝酸盐浓度)和temp(水域温度)是显著的,且根据回归系数可推断它们均有助于R. cataractae丰度的提升。排除了do2(水域溶解氧含量)和so4(水域硫酸盐浓度),这次的结论相比先前更加令人信服。
既然do2(水域溶解氧含量)和so4(水域硫酸盐浓度)不显著,不妨将它们从原回归模型中去除,使用剩余的环境变量重新拟合准泊松回归以简化模型,并重新解释在排除do2和so4协变量的情况下,各个环境变量对R. cataractae丰度的影响及效应。
#去除不显著的 do2(水域溶解氧含量)和 so4(水域硫酸盐浓度)后
#剩余 4 种显著的环境变量与鱼类物种丰度关系的准泊松回归
fit_quasipoisson2 <- glm(fish~acre+depth+no3+temp, data = dat, family = 'quasipoisson')
summary.glm(fit_quasipoisson2) #展示拟合回归的简单统计#fit_quasipoisson2 中,进一步观察到 temp(水域温度)不显著
#因此进一步优化模型
#去除 do2、so4 和 temp 后
#剩余 3 种显著的环境变量与鱼类物种丰度关系的准泊松回归
fit_quasipoisson3 <- glm(fish~acre+depth+no3, data = dat, family = 'quasipoisson')
summary.glm(fit_quasipoisson3) #展示拟合回归的简单统计

输出结果列出了回归系数、标准误和参数为0的检验,详情参考上文解读即可。
排除了do2(水域溶解氧含量)和so4(水域硫酸盐浓度)作为协变量影响后的新的准泊松回归模型中,进而发现temp(水域温度)不具有效应。
进一步排除do2、so4和temp后,最终获得了3个显著的环境变量,acre(流域面积)、depth(水域深度)和no3(硝酸盐浓度)均是显著影响R. cataractae丰度的因素,并根据回归系数得知它们均有助于R. cataractae丰度的提升。
类似地,前文“多元线性回归”中使用同样数据的线性回归结果也显示出R. cataractae丰度随这3个环境变量的数值增大而增长。
也就是最终的准泊松回归结果显示了与线性回归一致的趋势。回到最初的目的,是探索可能影响R. cataractae丰度的环境因素,并对其变化的原因作出解释。因为两个模型反映的生态响应趋势大致相同,您可以选择使用这里的准泊松回归用作生态解释,也可以选择先前的线性回归。相比之下,尽管线性回归更通俗直观,但准泊松回归原则上更适用于对此类物种丰度计数型数据的建模,更优先选择。
* 负二项回归
除了准泊松回归,处理偏大离差的另一种方法是使用负二项回归进行建模。负二项回归也是应用于计数型(非负整数)响应变量的回归模型,与泊松回归相比具有更大的灵活性,且被实践证明非常有效。
详情可参考前文“负二项回归应用举例和R计算”。
参考资料
Robert I. Kabacoff. R语言实战(第二版)(王小宁 刘撷芯 黄俊文 等 译). 人民邮电出版社, 2016.
钱松. 环境与生态统计:R语言的应用(曾思育 译). 高等教育出版社, 2011.