matlab计算机仿真与蒙特卡洛法【数学建模】

发布于

前言：在计算机出现之前，我们对数学模型的研究只能通过数学推导和实验研究两种方法。在此之后，我们可以通过在计算机上对实际问题的模拟、仿真求解模型。计算机仿真在数学建模中具有很重要的作用，而蒙特卡洛法则是计算机仿真中的一个重要方法。

一、计算机仿真

1.1定义：

计算计算机仿真根据已知的信息或知识，利用计算模拟现实情况或系统演变的过程，具有代价小、时间短、参数灵活等特点。

1.2计算机仿真两个关键步骤：

1、对系统关键数据的计算方法进行清晰表述。

2、对仿真的程序流程性表述。

下面看具体实例：

仿真实例1：追逐问题

如图：在正方形ABCD的四个顶点各有一个人。设初始时刻t=0,四人同时以速度v沿顺时针走向下一个人，如果他们始终对准下一个人为行进，结果会如何？请画出路线图。

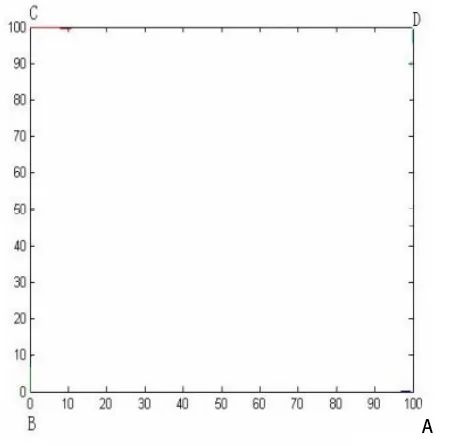
我们首先来看一下它的数学模型：

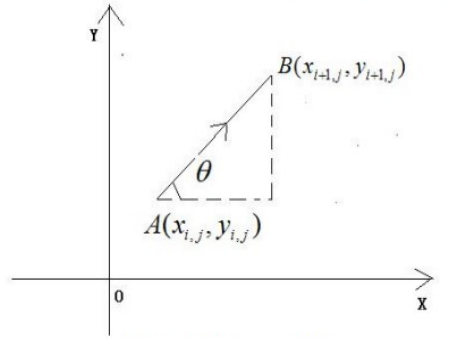
前三个人的运动的数学表达式为：

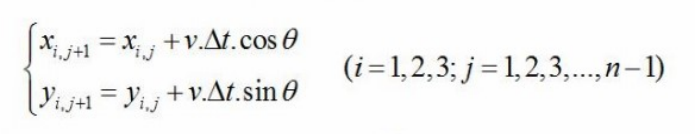
其中：

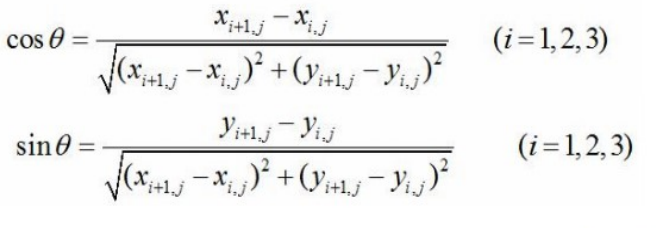
第四个人运动的数学表达式为：

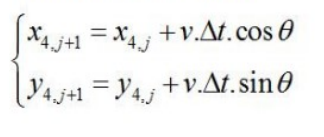
其中：

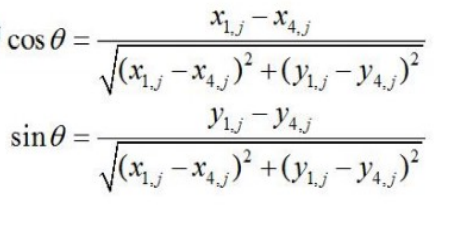
MATLAB仿真结果为：

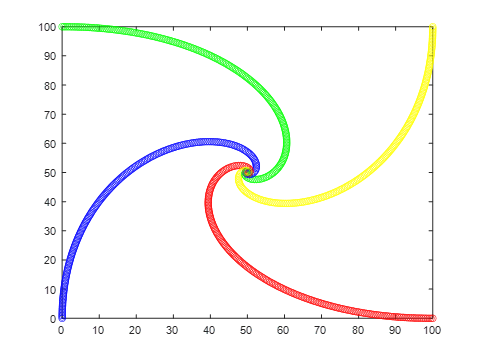
代码：

代码语言：javascript
复制
clc,clear,close
n = 240;
x = zeros(4,n);
y = zeros(4,n);
dt = 0.05;%时间间隔
v =10;%速度
x(1,1) = 100;y(1,1) = 0;%A的坐标
x(2,1) = 0;y(2,1) = 0;%B的坐标
x(3,1) = 0;y(3,1) = 100;%C的坐标
x(4,1) = 100;y(4,1) = 100;%D的坐标
for j = 1:n-1
    for i=1:3
        d = sqrt((x(i+1,j)-x(i,j))^2+(y(i+1,j)-y(i,j))^2);
        cosx = (x(i+1,j)-x(i,j))/d;
        sinx = (y(i+1,j)-y(i,j))/d;
        x(i,j+1) = x(i,j)+v*dt*cosx;
        y(i,j+1) = y(i,j)+v*dt*sinx;
    end
    %第D的坐标
    d = sqrt((x(1,j)-x(4,j))^2+(y(1,j)-y(4,j))^2);
    cosx = (x(1,j)-x(4,j))/d;
    sinx = (y(1,j)-y(4,j))/d;
    x(4,j+1) = x(4,j)+v*dt*cosx;
    y(4,j+1) = y(4,j)+v*dt*sinx;
    %运动图像
    plot(x(1,j),y(1,j),'ro',x(2,j),y(2,j),'bo',x(3,j),y(3,j),'go',x(4,j),y(4,j),'yo')
    hold on
end

二、蒙特卡罗法

通常蒙特卡罗方法可以粗略地分成两类：

一类是所求解的问题本身具有内在的随机性，并且这种随机性是存在一定的统计规律的，借助计算机可以直接模拟这种随机的过程。如排队问题中顾客到达的时间，顾客服务的时间都是具有统计规律的随机数，我们就可以用计算机产生这些随机数，进而模拟问题的解决过程，从而为决策提供支持。

另一种类型是所求解问题可以转化为某种随机分布的特征数，比如随机事件出现的概率，或者随机变量的期望值。通过随机抽样的方法，以随机事件出现的频率估计其概率，或者以抽样的数字特征估算随机变量的数字特征，并将其作为问题的解。如在计算不规则多边形的面积时，我们就可以在规则多边形中生成均匀分布的随机数，通过计算随机数出现在不规则多边形的面积的期望值来计算不规则多边形的面积。

仿真实例2：排队问题

在某商店有一个售货员，顾客陆续来到，售货员逐个地接 待顾客．当到来的顾客较多时，一部分顾客便须排队等待， 被接待后的顾客便离开商店．

假设：

1．顾客到来间隔时间服从参数为5的指数分布．

２．对顾客的服务时间服从［４，１５］上的均匀分布．

３．排队按先到先服务规则，队长无限制． 假定一个工作日为8小时，时间以分钟为单位。

要求模拟一个工作日内完成服务的个数及顾客平均等待时间t．

代码语言：javascript
复制
clc,clear
T = 8*60;
at = exprnd(5,[200,1]);%顾客间隔到达时间
st = unifrnd(4,15,[200,1]);%服务顾客所用时间
custmer = [at,st];
wt = zeros(200,1);%建立存储顾客等待时间
t = 0;
%模拟每天的排队情况
for i =1:200
    if t+custmer(1,1)>T
        n = i;
        break
    end
    t = custmer(i,2) + t;
    %模拟第i+1位顾客到达后，第i位顾客仍在办理业务的情况
    if i>1
        if custmer(i,1)<custmer(i-1,2)
            wt(i,1) = wt(i-1,1)+custmer(i-1,2)-custmer(i,1);
        end
    end
end
mt = round(sum(wt)/n);
disp((sprintf('顾客人数为：%d',n)))
disp((sprintf('平均等待时间为：%d',mt)))

仿真实例3：计算不规则多边形的面积

计算图中绿色部分的面积

代码语言：javascript
复制
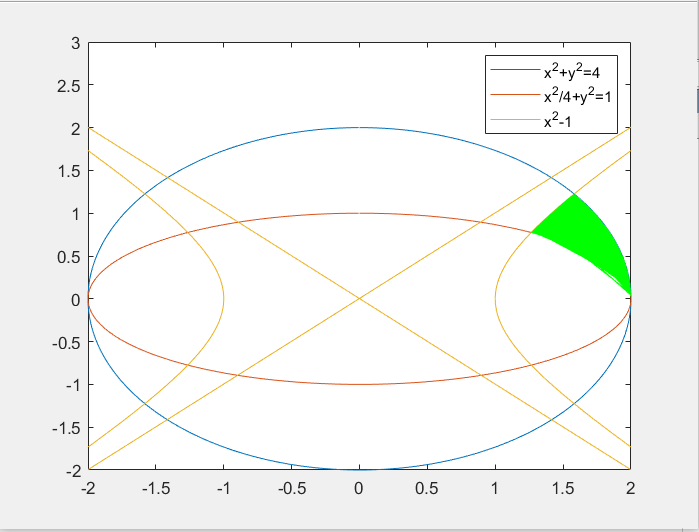
clc,clear
t=0:0.01:2*pi;
%把原方程转换为参数方程后再画图
plot(2*sin(t),2*cos(t),2*sin(t),cos(t),sec(t),tan(t))
axis([-2,2,-2,3])
hold on
%求解
n = 100000;%产生随机点的数目
p = rand(n,2);
x = p(:,1)+1;%横坐标范围
y = 2*p(:,2);%纵坐标范围
y1 = sqrt(4-x.^2);
y2 = sqrt(1-x.^2/4);
y3 = sqrt(x.^2-1);
L = find(y<=y1&y>=y2&y<=y3);
m = length(L); 
s = 2*m/n;%计算面积
plot(x(L),y(L),'g')
legend('x^2+y^2=4','x^2/4+y^2=1','x^2-1')

今天的内容就到这里，感谢您的阅读！如有问题，欢迎留言讨论，也欢迎向matlab爱好者投稿。

参考资料：

[1] 司守奎《数学建模算法与程序》

[2] 姜启源，谢金星，叶俊《数学建模》

[3] 包子阳，余继周《智能优化算法及其MATLAB实例》

#matlab#编程算法