计算机视觉 OpenCV Android | 图像操作之 统计排序滤波、边缘保留滤波

发布于
1.统计排序滤波

上节笔记中提到的均值模糊、高斯模糊两种图像模糊操作都属于图像的线性滤波， 本文则首先将笔记OpenCV中存在的几种基于统计排序的滤波器，即中值滤波、最大值与最小值滤波， 这几种滤波器在特定场合与应用场景下，也经常用来消除图像噪声或者抑制图像像素极小值与极大值。

1.1.中值滤波
  • 中值滤波同样也需要一个卷积核， 与卷积滤波不同的是，它不会用卷积核的每个系数与对应的像素值做算术计算， 而是把对应的像素值做排序，取中间值作为输出。

  • 具体说明如图所示：

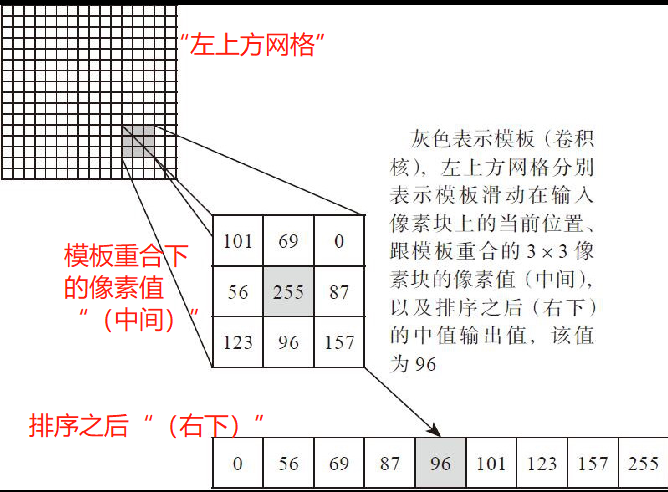
  • 线性滤波是一个自带有/设置有系数的“实”模板；
  • 中值滤波是有一个只有滤波特性，没有设置系数的“空”模板；
  • 运算逻辑顺序概况： “空”模板移动，套/捞与模板重合的N×N个像素值上来， 对套上来的值排序，取中值； 置回模板核中心格子下重合的像素块；

中值滤波的相关API函数处于Imgproc包中，完整的说明如下：

  • medianBlur(Mat src, Mat dst, int ksize) src：表示输入图像， 　　当ksize为3、5的时候输入图像可以为浮点数或者整数类型， 　　当ksize大于5的时候，则只能为字节类型图像，即CV_8UC。 dst：表示中值滤波以后输出的图像，其类型与输入图像保持一致。 ksize：表示上图中模板的大小， 常见为3、5，注意模板大小必须为奇数而且必须大于1。

调用此函数实现中值滤波的相关代码如下：

代码语言：javascript
复制
Mat src = Imgcodecs.imread(fileUri.getPath());
if(src.empty()){
　　return;
}
Mat dst = new Mat();
Imgproc.medianBlur(src, dst, 5);
代码语言：javascript
复制
划重点！！！
  • 中值滤波对图像的椒盐噪声有很明显的抑制作用，是一个很好的图像降噪的滤波函数。
代码语言：javascript
复制
！！！
1.2.最大值与最小值滤波
  • 最大值与最小值滤波和中值滤波极其相似， 唯一不同的就是对于排序之后的像素数组， 前两者分别用最大值或者最小值来取代中心像素点作为输出；

  • 具体说明如图所示（与上面中值滤波的解释类似）：

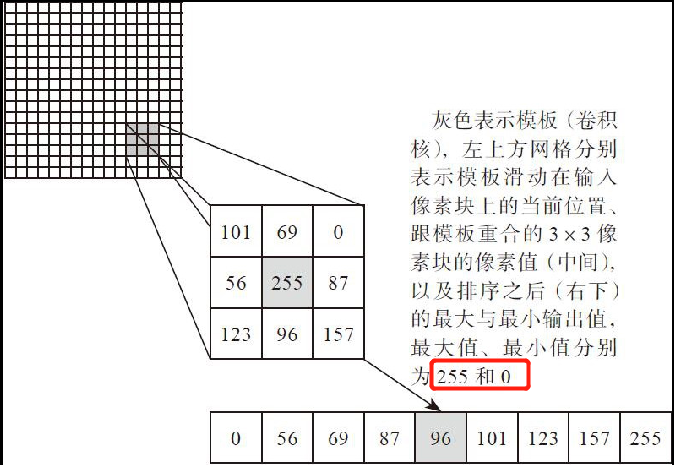
  • OpenCV没有以max或min单词开头来命名的最大或者最小值滤波函数， 而是通过两个形态学操作函数来替代实现最大值与最小值滤波。 它们分别是dilate与erode。

对于这两个函数的说明具体如下：

  • dilate(Mat src, Mat dst, Mat kernel) //膨胀(最大值滤波)用最大值替换中心像素 src：表示输入图像。 dst：表示输出图像。 kernel：表示结构元素或者卷积核，注意它可以是任意形状。
  • erode(Mat src, Mat dst, Mat kernel) //腐蚀(最小值滤波)用最小值替换中心像素 src：表示输入图像。 dst：表示输出图像。 kernel：表示结构元素或者卷积核，注意它可以是任意形状。

其中结构元素/卷积核的获取代码如下：

代码语言：javascript
复制
Mat kernel = Imgproc.getStructuringElement(Imgproc.MORPH_RECT, new Size(3, 3));

上述代码将会生成一个3×3大小的矩形结构元素。 使用该结构元素实现最大值或者最小值滤波的代码如下：

代码语言：javascript
复制
Mat src = Imgcodecs.imread(fileUri.getPath());
if(src.empty()){
return;
}
Mat dst = new Mat();
Mat kernel = Imgproc.getStructuringElement(
　　　　　　　　　　　　　Imgproc.MORPH_RECT, new Size(3, 3));
// Imgproc.dilate(src, dst, kernel);
Imgproc.erode(src, dst, kernel);
  • 统计排序滤波器是最简单的非线性滤波器， 它可以帮助我们抑制图像中特定类型的噪声， 是非常有用的图像滤波器。
2. 边缘保留滤波
  • 除了上面提到的统计排序滤波器， 还有一类滤波器也是非线性滤波， 它们的实现算法各有不同，但作用却是惊人的相似， 这类滤波通常称为图像边缘保留滤波。

OpenCV中已经实现的边缘保留滤波有高斯双边滤波、金字塔均值迁移滤波， 它们无一例外都拥有类似于人脸美化或者图像美化的效果，是很好的图像边缘保留滤波（EPF）方法。

下面笔记这两种滤波方法的基本原理以及与它们对应的函数。

2.1. 高斯双边滤波

在开始读书笔记之前，这里先做一个总结， 概况一下高斯滤波以及高斯双边滤波，分析其区别： （高斯滤波部分内容与上一篇笔记重复）

  • 正态分布与高斯分布？ 正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。
  • 关于高斯分布的知乎参考
  • 高斯滤波（高斯模糊） 高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。

    通俗的讲，
    高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。

    高斯滤波的具体操作是:用一个模板(或称卷积、掩模)扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

    　- 好处
    高斯平滑滤波器对于抑制服从正态分布（高斯分布）的噪声非常有效。
    　- 缺憾
    对于高频细节的保护效果并不明显，没有做边缘保护。

  • 高斯双边滤波（百度百科解释） 双边滤波(Bilateral filter)是一种非线性的滤波方法， 是结合图像的空间邻近度和像素值相似度的一种折衷处理， 同时考虑空域信息和灰度相似性， 达到保边去噪的目的。 具有简单、非迭代、局部的特点。

    　- 好处
    可以做边缘保存(edge preserving)，
    一般过去用的维纳滤波或者高斯滤波去降噪，都会较明显地模糊边缘，对于高频细节的保护效果并不明显。
    双边滤波器顾名思义比高斯滤波多了一个高斯方差sigma-d，
    它是基于空间分布的高斯滤波函数，
    所以在边缘附近，离的较远的像素不会太多影响到边缘上的像素值，这样就保证了边缘附近像素值的保存。
    　- 缺憾
    由于保存了过多的高频信息，
    对于彩色图像里的高频噪声，
    双边滤波器不能够干净的滤掉，只能够对于低频信息进行较好的滤波。

（下面切回读书笔记）

  • 高斯双边滤波 是在高斯滤波的基础上进一步拓展与延伸出来的图像滤波方法，
    blur操作是图像均值模糊，会导致图像出现轮廓与边缘消失的现象，
    而高斯模糊则会产生类似于毛玻璃的效果，导致边缘扩展效应明显、图像边缘细节丢失的问题。
  • 双边滤波器（Bilateral Filter）可以在很好地保留边缘的同时，抑制平坦区域图像的噪声。
    双边滤波器能做到这些，
    （划重点！！****************************************************************************************）
    原因在于它不像普通的高斯/卷积低通滤波，
    其不仅考虑了位置对中心像素的影响，
    还考虑了卷积核中像素与中心像素之间相似程度的影响，
    据说，Adobe Photoshop的高斯磨皮功能就是应用了此技术。

下图形象地解释了高斯双边滤波的原理：

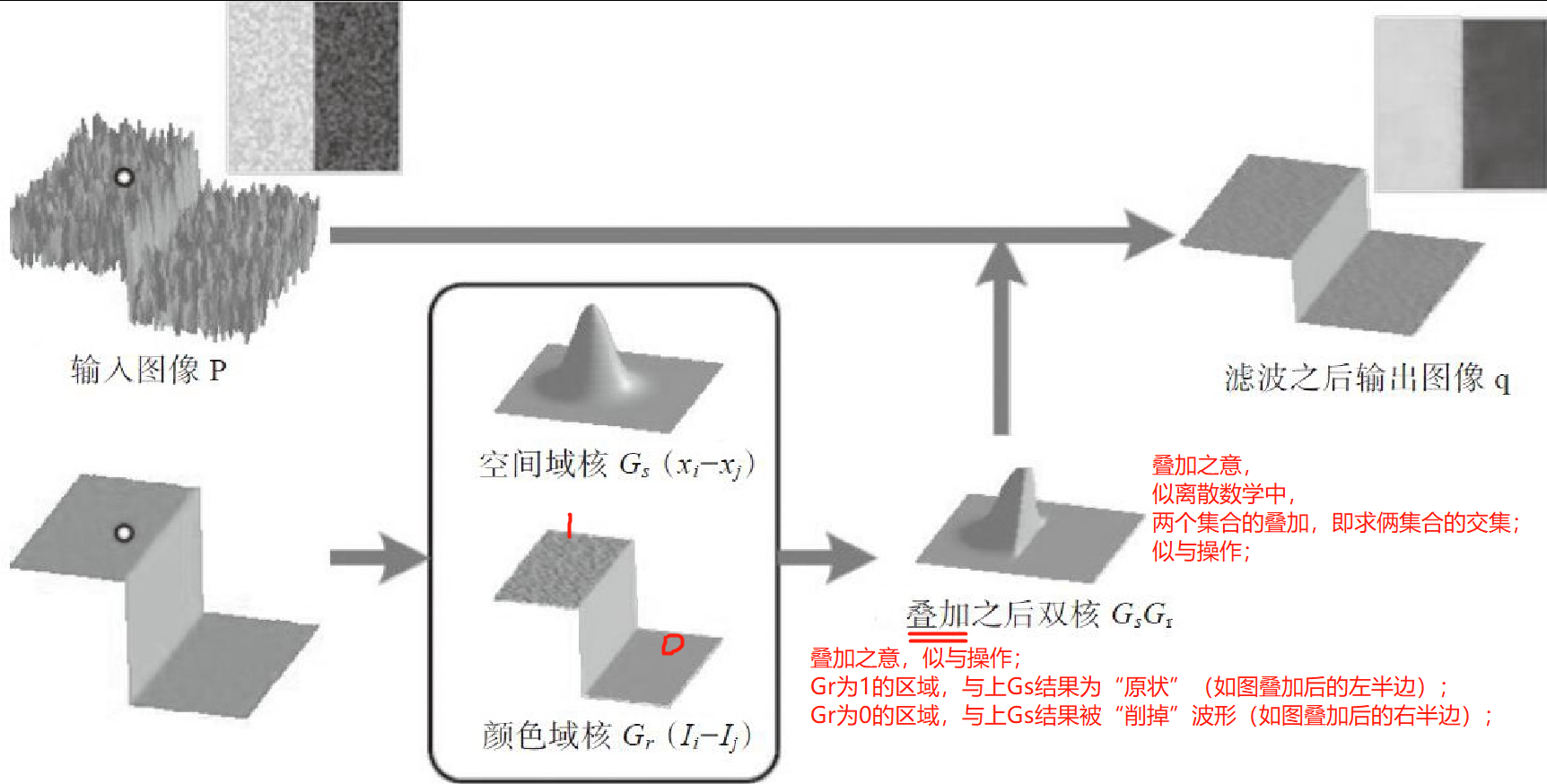
高斯双边滤波的函数为：

  • bilateralFilter(Mat src, Mat dst, int d, double sigmaColor, double sigmaSpace) src：表示输入图像。 dst：表示输出图像。 d：表示用来过滤的卷积核直径大小， 　　一般取0，意思是从sigmaColor参数自动计算。 sigmaColor：颜色权重计算时候需要的参数。 sigmaSpace：空间权重计算时候需要的参数。
  • 通常情况下， sigmaColor的取值范围在100～150左右， sigmaSpace的取值范围在10～25之间的时候， 双边滤波的效果比较好，调用函数时的速度也会比较快。
  • 使用该函数实现图像双边滤波的代码如下：
代码语言：javascript
复制
Mat src = Imgcodecs.imread(fileUri.getPath());
if(src.empty()){
return;
}
Mat dst = new Mat();
Imgproc.bilateralFilter(src, dst, 0, 150, 15);
2.2 均值迁移滤波
  • 均值迁移滤波主要是通过概率密度估算与中心迁移的方式来实现图像边缘保留滤波， 其基本原理是通过创建大小指定的卷积核窗口， 搜索并计算该窗口中心像素P（x，y）范围内所有满足条件的像素， 计算它们的中心位置， 然后基于新中心位置再次计算更新， 直到中心位置不再变化或者两次变化的中心的距离满足指定的收敛精度值为止。

一个更直观的图示如下所示：

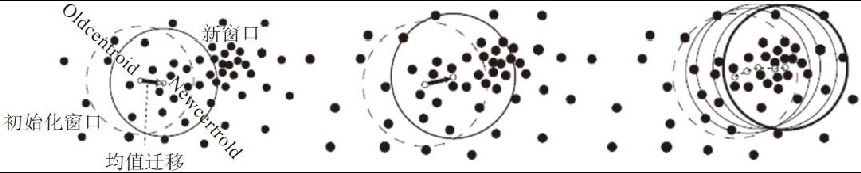
上图中的虚线圆是前一个迭代的窗口位置与中心， 实线圆是当前的窗口与中心， 可以看出随着迭代计算中心的不断迁移，重心位置越来越趋近高密度区域， 直到稳定为止。

OpenCV中均值迁移滤波函数处于Imgproc模块中， 其还可以被用作图像自动分割方法之一，

解释具体如下： pyrMeanShiftFiltering(Mat src, Mat dst, double sp, double sr, int maxLevel, TermCriteria termcrit) src：输入图像。 dst：输出图像。 sp：图像色彩空间，也是窗口大小。 sr：图像色彩像素值范围，也是像素差值范围。 maxLevel：表示金字塔的层数，当maxLevel大于0的时候，金字塔层数为Level+1。 termcrit：表示循环或者迭代停止条件。

通常最后两个参数使用默认值即可，无须再次显式声明。

使用该函数的代码：

代码语言：javascript
复制
Imgproc.pyrMeanShiftFiltering(src, dst, 10, 50);

  • 补充：关于maxLevel的金字塔的层数的意义以及termcrit的解释等， 可以 点击这里 去官网终究查个明白；

  • 下面是官网上对应的截图（先后是原版英文版以及谷歌翻译中文版）：

  • 除了OpenCV实现的这两种常用的边缘保留滤波方法之外， 常见的边缘保留滤波方法还包括 图像各向异性滤波、局部均方差滤波、导向滤波等， 感兴趣的小伙伴可以阅读相关的资料。
#opencv#kernel