引言
在之前的章节中,我们已经详细介绍了计算机硬件的组成部分,包括中央处理器(CPU)、内存、磁盘和总线等。因此,从今天开始,我们将深入探讨计算机内部的工作原理。首先,我们将从二进制这个简单而重要的概念开始讲解,因为计算机底层只能使用二进制来表示和处理信息。
二进制
我们都知道,计算机的底层使用二进制数据进行数据流传输。那么,为什么计算机要使用二进制表示呢?又什么是二进制数呢?更进一步地,我们如何使用二进制进行加减乘除运算呢?接下来,我们将一一解答这些问题。
什么是二进制数
那么,什么是二进制数呢?为了详细说明这个问题,我们先将一个二进制数 00100111 转换为十进制数进行观察。将二进制数转换为十进制数的方法是,直接将各个位置上的值乘以相应的位权,然后相加得到结果。那么,让我们来将上述的二进制数转换为十进制数。

根据转换规则,将二进制数 00100111 转换为十进制数,结果为 39。这里的 39 不是由数字 3 和 9 连在一起写成的,而是由 3 乘以位权 10 和 9 乘以位权 1 相加得到的。而这些位权,从高位到低位依次为 7、6、5、4、3、2、1、0。这些位权也可以被称为次幂,例如最高位的位权就是 2 的 7 次幂,第二位的位权就是 2 的 6 次幂,以此类推。
在二进制数的运算中,每次运算都是以基数 2 作为底数。而十进制数的基数则是 10。在任何情况下,位权的值都是数的位数减去 1。因此,第一位的位权为 1 - 1 = 0,第二位的位权为 2 - 1 = 1,以此类推。
移位运算和乘除的关系
在我们了解了二进制数之后,接下来让我们来探讨一下二进制数的运算。和十进制数一样,二进制数也可以进行加减乘除运算,只需要注意到逢二进位即可。二进制数的运算是计算机程序中的基础运算,因此了解二进制的运算是至关重要的。
首先,让我们来介绍一下移位运算。移位运算是指将二进制数的各个位置上的元素进行左移和右移操作。具体的操作可以参考下图:
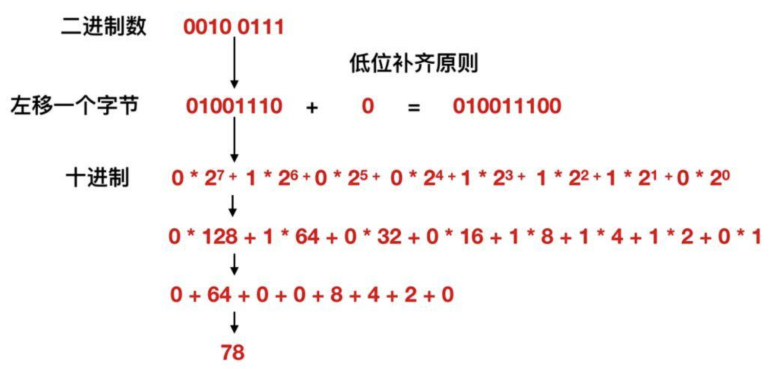
移位运算在计算机中被广泛应用,可以用于快速进行乘以或除以2的幂次的运算。同时,移位运算也可以用来提取或插入二进制数中的特定位。
除了移位运算,还有其他的二进制运算,如按位与、按位或、按位异或等。这些运算可以用于处理和操作二进制数据,在计算机科学中有着重要的应用。
补数
刚才我们没有介绍右移的情况,是因为右移之后空出来的高位数值有两种形式:0和1。为了区分补0和补1的情况,我们需要了解二进制数表示负数的方法。
一般来说,二进制数中用最高位作为符号位来表示负数。符号位为0表示正数,为1表示负数。那么如何用二进制数表示-1呢?很多人可能会认为,因为1的二进制是0000 0001,最高位是符号位,所以-1应该表示为1000 0001。但是这个答案是否正确呢?
实际上,计算机中没有减法运算,计算机在做减法时实际上是通过加法来实现的,即用加法来表示减法运算。例如100-60,在计算机中实际上看作是100+(-60)。为了表示负数,我们需要使用二进制补码,即用正数表示负数。
为了得到补码,我们需要将二进制的各位数值全部取反,然后再加1。记住这个结论因为他适用于所有负数,下面我们来演示一下。

具体来说,要获取某个数值的二进制补码,需要先获取该数值的二进制表示,然后对每一位进行取反操作(0变为1,1变为0),最后再将取反后的数值加1,这样就得到了补码。
尽管补码的获取可能在直观上不容易理解,但在逻辑上是非常严谨的。举个例子,我们来看一下1-1的过程。我们先用上面提到的1000 0001(我们假设它是1的补码,如果不了解,请参考前文,先不管补码是否是对的)来表示一下。
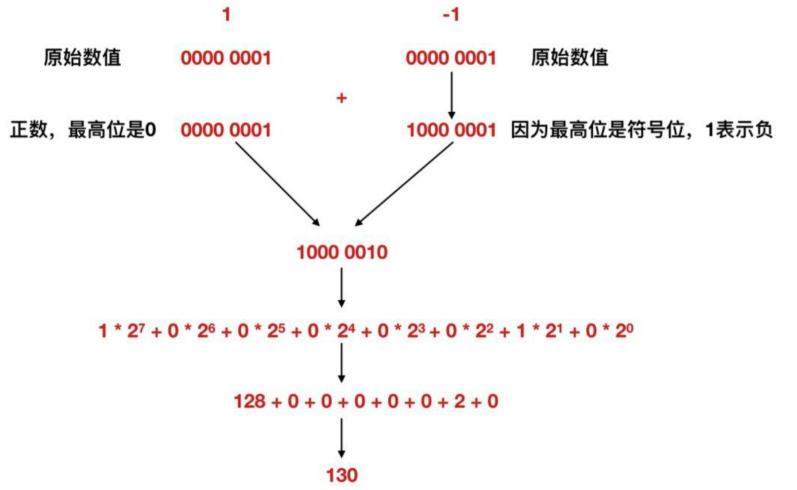
奇怪,1 - 1 为什么会变成 130 而不是 0?这个结果看起来很奇怪,我们来分析一下。
对于正数 1,它的二进制表示是 0000 0001。现在我们将其转成补码。首先取反各位得到 1111 1110,然后加1,得到补码 1111 1111,即 -1 的补码表示。
接下来,我们来验证一下 -1 的补码表示是否正确。
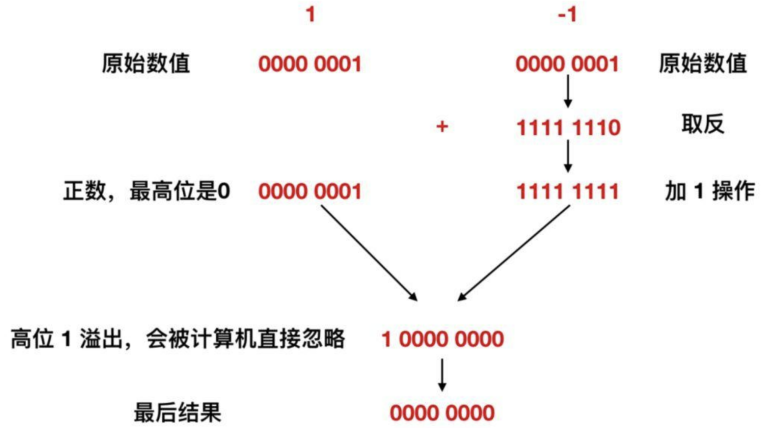
我们可以观察到,1 - 1 实际上是 1 + (-1) 的运算。对于 -1,我们可以使用上面提到的方法来求其补码表示。通过取反 + 1 的过程,我们得到了补码 1111 1111。然后,将补码 1111 1111 与 1 进行加法运算。
在加法运算中,我们会得到一个九位的结果 1 0000 0000。然而,在计算机中,发生了溢出的情况下,会直接忽略掉溢出位,即最高位的 1。因此,结果变为 0000 0000,即 0。所以,我们得出的结果是正确的,1111 1111 表示的是 -1。
综上所述,负数的二进制表示是通过先求其补数,即对原始数值的二进制数各位取反,然后将结果加1。这样可以得到正确的负数的二进制表示。
算数右移和逻辑右移的区别
在了解了补数的概念之后,我们需要重新考虑一下右移这个问题。右移操作会导致最高位出现两种情况,即0和1。
当我们将二进制数作为带符号的数值进行右移运算时,移位后需要在最高位填充移位前的符号位的值(0或1)。这种右移方式被称为算术右移。如果数值是负数且使用补码表示,那么右移后需要在最高位补1,这样才能正确地表示数值的1/2、1/4、1/8等运算结果。而如果是正数,则直接在最高位补0即可。
下面我们来看一个右移的例子,将-4右移两位,大家可以参考移位示意图来理解。
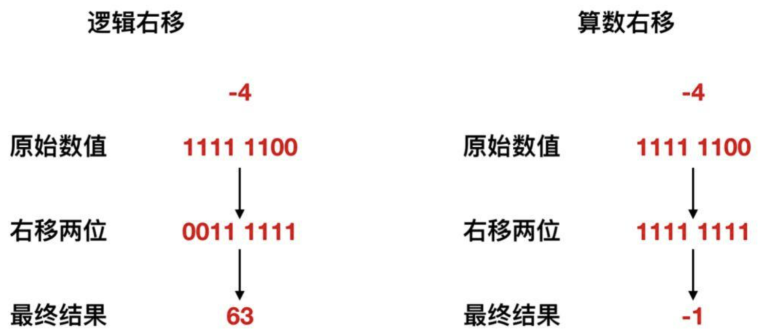
根据上图所示,当进行逻辑右移操作时,-4右移两位会变成63,显然这不是它的1/4,因此逻辑右移不适用于这种情况。而在算数右移的情况下,-4右移两位会变为-1,显然这是它的1/4,所以我们选择采用算数右移。
因此,我们可以得出一个结论:在左移操作中,无论是正数还是负数,只需要将低位补0即可;而在右移操作中,需要根据具体情况判断是应该进行逻辑右移还是算数右移。
现在我要介绍一下符号扩展的概念。符号扩展是为了在保持数值不变的前提下,增加数据的位数,以满足某些指令对操作数位数的要求。它可以用于使被除数比除数位数更长,或者用于增加数据位数以减少计算过程中的误差。
以8位二进制数为例,符号扩展的目标是将其转换为16位或32位二进制数,而保持数值不变。对于一个8位正数二进制数0111 1111,很容易得到正确的16位结果0000 0000 0111 1111。但对于一个用补码表示的负数,比如补码1111 1111,我们该如何处理呢?我们只需要直接将其表示为16位二进制数1111 1111 1111 1111。换句话说,无论是正数还是补码表示的负数,只需要在高位填充0或1即可。
总结
通过本文的学习,我们深入了解了计算机内部工作原理中的二进制数、移位运算、补数表示、算术右移和逻辑右移等重要概念。我们了解到计算机底层使用二进制来表示和处理信息的原因,并学习了二进制数的转换方法和位权的概念。我们还探讨了移位运算和二进制数的运算,并介绍了移位运算在计算机中的应用。此外,我们学习了二进制补数的概念和计算方法,以及符号扩展的原理和应用。最后,我们讨论了算术右移和逻辑右移的区别,并总结了在左移和右移操作中应该采用的补位方法。通过本文的学习,我们对计算机内部工作原理有了更深入的了解,为进一步学习和研究计算机科学打下了坚实的基础。
我正在参与2023腾讯技术创作特训营第四期有奖征文,快来和我瓜分大奖!