《程序员数学：欧几里德算法》—— 如何编码程序计算最大公约数

作者：小傅哥博客：https://bugstack.cn

❝沉淀、分享、成长，让自己和他人都能有所收获！😜 ❞

一、前言
二、短除法
三、欧几里德算法
四、辗转相除法代码实现
- 1. 循环实现
- 2. 递归实现
- 3. 测试验证
五、常见面试题

一、前言

嘿，小傅哥怎么突然讲到最大公约数了？

这么想你肯定是没有好好阅读前面章节中小傅哥讲到的RSA算法，对于与欧拉结果计算的互为质数的公钥e，其实就需要使用到辗转相除法来计算出最大公约数。

放心，你所有写的代码，都是对数学逻辑的具体实现，无非是难易不同罢了。所以如果你真的想学好编程思维而不只是CRUD，那就要把数据结构、算法逻辑等根基打牢。

二、短除法

既然都说到这了，那你还记得怎么计算最大公约数吗，死鬼？

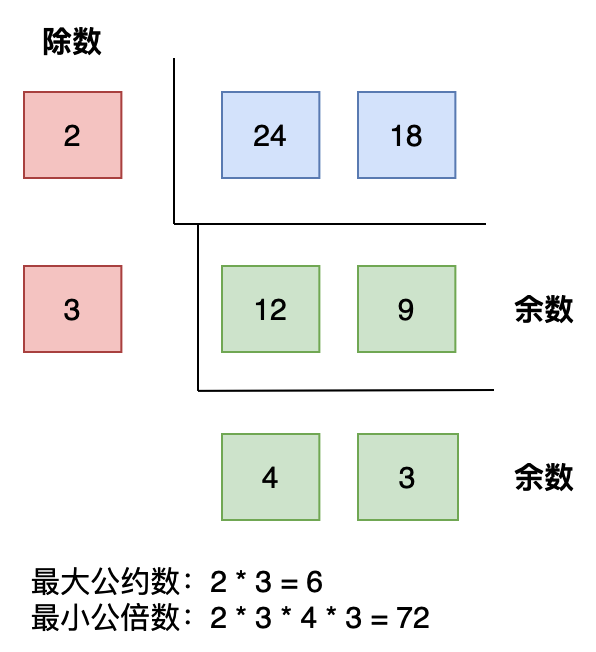
以上这种方式就是我们在上学阶段学习的，这种计算方式叫做短除法。

短除法：是算术中除法的算法，将除法转换成一连串的运算。短除法是由长除法简化而来，当中会用到心算，因此除数较小的除法比较适用短除法。对大部分的人而言，若除以12或12以下的数，可以用记忆中乘法表的内容，用心算来进行短除法。也有些人可以处理除数更大的短除法。—— 来自维基百科

三、欧几里德算法

短除法能解决计算最大公约数的问题，但放到程序编写中总是很别扭，总不能一个个数字去试算，这就显得很闹挺。其实除了短除法还有一种是计算公约数的办法，叫做欧几里德算法。

欧几里德算法：是计算两个整数（数字）的最大公约数【GCD(Greatest Common Divisor)】的有效方法，即能将它们整除而无余数的最大数。它以古希腊数学家欧几里得的名字命名，欧几里德在他的几何原本（约公元前 300 年）中首次描述了它。它是算法的示例，是根据明确定义的规则执行计算的分步过程，并且是常用的最古老的算法之一。它可以用来减少分数到他们的最简单的形式，并且是许多其他数论和密码计算的一部分。—— 来自维基百科

GCD，代表了两个数字的最大公约数，GCD(X,Y) = Z，那么就表示 X 和 Y 的最大公约数是 Z。由欧几里德算法给出 GCD(X,Y) = GCD(Y,XmodY) —— mod 表示求模计算余数。

其实简单来说就是，X和Y的公约数是Z，那么Y和Z的公约数也是Z。24和18的最大公约数是6，那么18和6的公约数也是6。嘿，就这么一个事。但就因为有了这一样一条推论，让编程代码变得优雅舒服，只需要不断地将X、Y两数作差，就能计算最大公约数。

😂 这让小傅哥想起，多年前上学时候，我也给出过一条推论；”任意一组所能构成等差数列的三个数字，所能组合出来的一个三位数，都能被3整除。“ 例如：等差数列 16、31、46 组合成三位数 463116 或者 461631 都能被3整除。

四、辗转相除法代码实现

欧几里德算法 = 辗转相除法法：https://en.wikipedia.org/wiki/Euclidean_algorithm

在辗转相除法的实现中，计算最大公约数的方式，就是使用一个数字减去另外一个数字，直到两个数字相同或者有其中一个数字为0，那么最后不为零的那个数字就是两数的最大公约数。

小傅哥在这里提供了2种计算方式，一种是循环另外一种是递归。—— 方便很多看不懂递归的小伙伴可以用另外的方式学习。

1. 循环实现

代码语言：javascript

复制

public long gcd01(long m, long n) {
    m = Math.abs(m);
    n = Math.abs(n);
while (m != 0 &amp;&amp; n != 0 &amp;&amp; m != n) {
    if (m &gt; n) {
        m = m - n;
    } else {
        n = n - m;
    }
}
return m == 0 ? n : m;

}

两数循环处理中，条件为 m != 0 && n != 0 && m != n 直至循环结束。

2. 递归实现

代码语言：javascript

复制

public long gcd02(long m, long n) {

if (m < n) {

long k = m;

m = n;

n = k;

}

if (m % n != 0) {

long temp = m % n;

return gcd02(n, temp);

} else {

return n;

}

}

计算方式逻辑和条件是一样的，只不过这个是使用了递归调用的方式进行处理。

3. 测试验证

代码语言：javascript

复制

@Test

public void test_euclidean() {

Euclidean euclidean = new Euclidean();

System.out.println(euclidean.gcd01(124, 20));

System.out.println(euclidean.gcd02(124, 20));

}

测试结果

代码语言：javascript

复制

4 4

Process finished with exit code 0

计算 124 和 20 的最大公约数，两个计算方式结果都是 4 。好的，到这测试通过。
这并不是一个很难的知识点，但当你做一些技术分享、答辩述职等时候，能这样用技术语言而不是大白话的讲述出来后，其实高度就有了。兄弟！👬🏻

五、常见面试题

最大公约数的使用用途？
如何使用代码实现最大公约数计算？
你是否了解欧几里德算法？
关于数论你还记得多少？
RSA 加密算法为什么需要用到公约数计算？

欧几里德算法：https://en.wikipedia.org/wiki/Euclidean_algorithm
线性组合：https://en.wikipedia.org/wiki/Linear_combination
贝祖定理：https://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity

- END -

你好，我是小傅哥。一线互联网java 工程师、T8架构师，开发过交易&营销、写过运营&活动、设计过中间件也倒腾过中继器、IO板卡。不只是写Java语言，也搞过C#、PHP，是一个技术活跃的折腾者。