计算机组织结构(四) 浮点数四则运算

发布于

📚 文档目录 合集-数的二进制表示-定点运算-BCD 码-浮点数四则运算-内置存储器-Cache-外存-纠错-RAID-内存管理-总线-指令集: 特征- 指令集:寻址方式和指令格式

浮点数的加减运算

X=X_S \times 2^{X_E},Y=Y_S \times 2^{Y_E}

  • 步骤
    1. 检查是否为零
    2. 阶码对齐,尾数移位
    3. 对尾数加或减
    4. 标准化结果
    5. 溢出判断
  1. 对阶 求阶差\Delta E=\begin{cases} =0,已经对齐\\\ne0,\begin{cases}大的向小的对齐:减小较r大的阶码,同时扩大其尾数\\小的向大的对齐:增大较小的阶码,同时减小其尾数 \end{cases} \\\end{cases}在计算机中,尾数左移可能会使最高位数据丢j失,故采用小阶向大阶对齐 浮点数加减的过程

一些溢出情况

1. Exponent overflow
  • 一个正的指数超出了指数的最大值(即127)
  • 指定为-\infty 或 +\infty
2. Exponent underflow
  • 一个负的指数小于了指数的最小值(即-126)
  • 指定为0.
3. Significand overflow
  • 同号的两个数字相加时,在最重要的位上产生了进位.
  • 在realignment时修正
4. Significand underflow
  • 在对齐尾数的时候, 数据可能从尾数的最右端流失
  • 需要某种形式的四舍五入

原码加减法(用于尾数的加减)

  • 如果两个操作数符号相同,做加法,否则做减法. 加法: 若最高位产生了进位,溢出 符号同加数 减法:加第二个数的补数 若最高位产生进位,结果正确(符号等同于被减数) 若没有进位,应该取结果的补数,最终结果与被减数相反.注意:此处可以是认定为没有符号位的补码在做计算,所以最终结果需要进行修正.(因为正数补码是它自身,负数补码是其反码加一) 更通俗的说法:最终算A+B的时候(无论是一开始就是A+B还是减法转化而来).如A,B同号,尾数是正常相加;若A,B异号,尾数为A_S+[B_S]_补

浮点数加减法举例

  • 减法 0.5-(-0.4375)=0.5+0.4375=0.9375 0.5   0 01111110 00000000000000000000000 -0.4375 1 01111101 11000000000000000000000  0.4375 0 01111101 11000000000000000000000 01111110-01111101=01111110+10000011=00000001 则前者阶码比后者大,后者向前者对齐(后者阶码加1,尾数右移一位,此处尾数包含隐藏位，即橙色位).减法经处理后,两个操作数同号,尾数做正常加法

加法计算没有进位，则结果正确，为

  • 加法 0.5+(-0.4375)=0.0625 0.5   0 01111110 00000000000000000000000 -0.4375 1 01111101 11000000000000000000000 01111110-01111101=01111110+10000011=00000001 则前者阶码比后者大,后者向前者对齐(后者阶码加1,尾数右移一位,此处尾数包含隐藏位，即橙色位).两个操作数异号,尾数加法做加后者补数.

符号相异产生进位,结果正确,与第一个操作数符号相同.经规格化后:

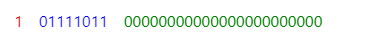
浮点数乘法

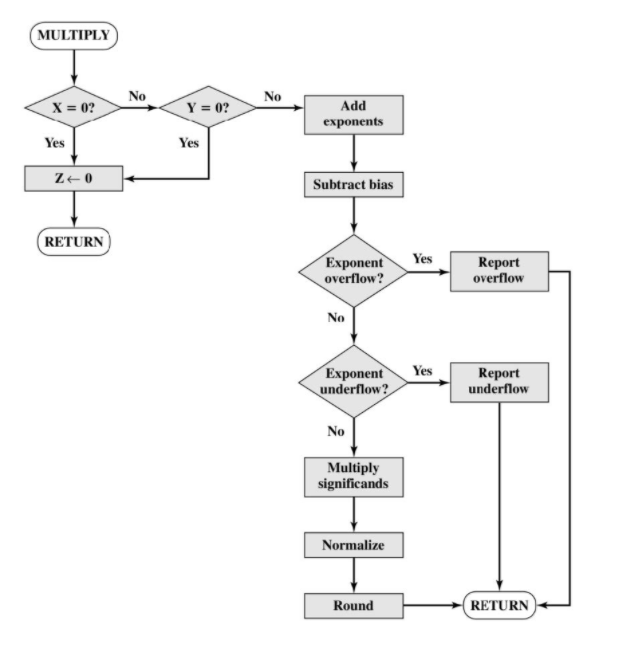
  • 步骤
    • 如果任何一个操作数为0,返回0.
    • 指数相加时需要减去偏差值,因为阶码用移码表示.
    • 尾数相乘.
    • 结果规格化并舍入.(可能造成指数溢出).

浮点数除法

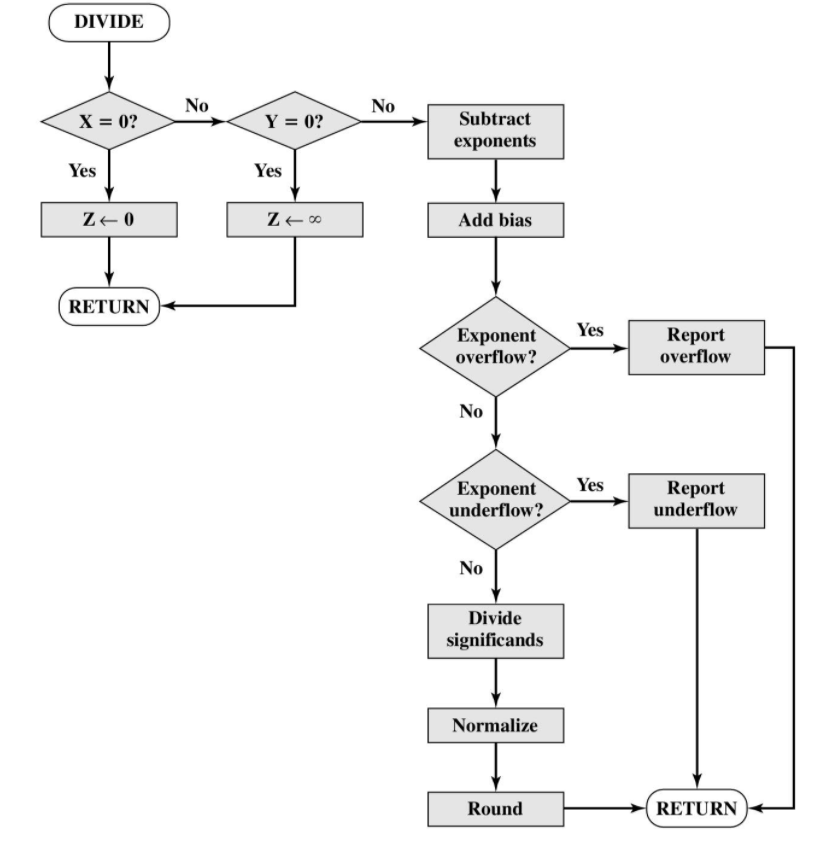
  • 步骤
    • 除数为0,报错或设为无穷.
    • 被除数为0,设为0.
    • 被除数的阶码和除数的阶码做差,并加回偏差值.
    • 尾数相除.
    • 结果标准化并舍入.

注意:和无符号整数除法不同:浮点数除法给被除数后面填零存入余数和商寄存器,而整数是高位填零.

保护位

为了提高精度,在计算时每个数字都存在保护位,暂时储存着计算后(比如右移)后的超出低位的数据.

#overflow