使用开源量子编程框架ProjectQ进行量子计算资源估计与绘制量子线路图

技术背景

在量子计算领域，基于量子芯片的算法设计(或简称为量子算法)是基于量子线路来设计的，类似于传统计算中使用的与门和非门之类的逻辑门。因此研究一个量子线路输入后的编译(可以简化为数量更少的量子门组合，或者适配硬件上可实现的量子逻辑门操作)，并且输出编译后的量子线路与量子线路图，在各种场景下都会使用到。而且，量子线路编译也能够为量子计算资源估计带来更加准确的结果预测。

量子计算与量子线路

针对于量子计算，这里我们尽量的避免硬件上实现原理的解释，因为那是属于另外一个领域的研究课题。这里我们仅从矩阵力学的角度来理解，读者可以尝试从这篇介绍量子系统模拟的博客中先了解一部分量子门操作的实现。这些量子门的每一种排列组合，我们都可以将其视为一个量子线路，如下图所示是一种量子线路的图示。

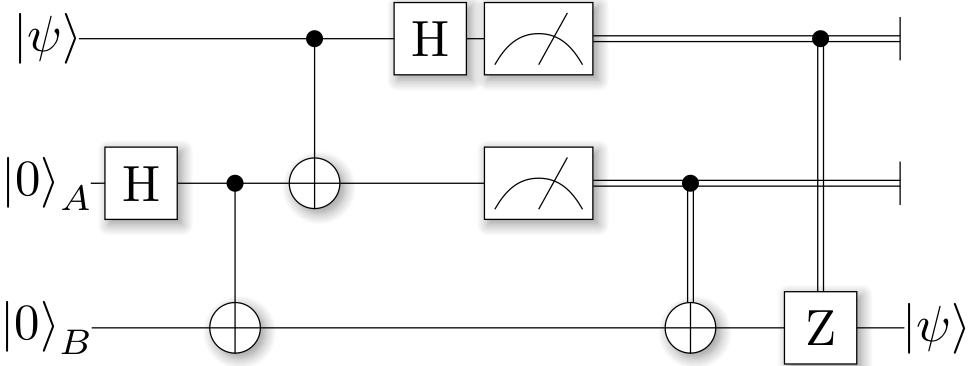
这里的

门和

CNOT

门作用在不同的量子比特上，相当于执行了一项如下所示的任务：

[\left|\psi_t\right>=U\left|\psi_0\right> ]

这里将

作用在初始的量子态

\left|\psi_0\right>

之后得到了一个新的量子态

\left|\psi_t\right>

，当然，此时信息还被存储在量子态中。如果需要将量子态中的信息读取到经典信息，就需要对量子态进行采样，相关过程可以参考这篇介绍量子态采样的博客，最终我们得到的信息是一系列二进制比特串的分布。

ProjectQ编译与打印量子线路

我们先用ProjectQ量子编程框架写一个不会被编译优化的量子线路：

代码语言：javascript

复制

from projectq import MainEngine
from projectq.backends import CommandPrinter
from projectq.ops import H, CX, X, Z, Measure, All
circuit_backend = CommandPrinter()

eng=MainEngine(backend=circuit_backend)
qubits = eng.allocate_qureg(3)

All(H) | qubits

CX | (qubits[0], qubits[1])

CX | (qubits[1], qubits[2])

eng.flush()

这个程序的基本逻辑是：使用MainEngine类来执行编译优化等工作;使用CommandPrinter作为后端，表示只打印量子线路而不进行计算;分配3个量子比特进行计算，最后作用一个线路在该量子系统上。这个程序的执行输出如下，是一个包含有Allocate的量子线路：

代码语言：javascript

复制

Allocate | Qureg[0]

H | Qureg[0]

Allocate | Qureg[1]

H | Qureg[1]

CX | ( Qureg[0], Qureg[1] )

Allocate | Qureg[2]

H | Qureg[2]

CX | ( Qureg[1], Qureg[2] )

这里在额外介绍几种优化操作：量子比特回收和量子线路编译。由于该分配的比特已经在内存中注册，需要手动的注销该量子系统所分配的量子比特：

代码语言：javascript

复制

from projectq import MainEngine

from projectq.backends import CommandPrinter

from projectq.ops import H, CX, X, Z, Measure, All
circuit_backend = CommandPrinter()

eng=MainEngine(backend=circuit_backend)

qubits = eng.allocate_qureg(3)
All(H) | qubits

CX | (qubits[0], qubits[1])

CX | (qubits[1], qubits[2])

eng.flush(deallocate_qubits=True)

这里python代码中唯一的变化就是增加了deallocate_qubits=True这个选项，最终输出的量子线路里面也就会包含有Deallocate的操作：

代码语言：javascript

复制

Allocate | Qureg[0]

H | Qureg[0]

Allocate | Qureg[1]

H | Qureg[1]

CX | ( Qureg[0], Qureg[1] )

Deallocate | Qureg[0]

Allocate | Qureg[2]

H | Qureg[2]

CX | ( Qureg[1], Qureg[2] )

Deallocate | Qureg[1]

Deallocate | Qureg[2]

如果在线路中遇到一些可以简化的模块，比如连续作用两次H门之后，相当于没有执行任何的操作，即

HH=I

。这里的

的矩阵形式如下所示：

[H=\left( \begin{array}{l} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\ \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \end{array} \right) ]

如下代码所示我们除了在所有量子比特上作用

门之外，在第二个量子比特上额外作用一个

门，这样理论上说两次连续作用的

门会被抵消：

代码语言：javascript

复制

from projectq import MainEngine

from projectq.backends import CommandPrinter

from projectq.ops import H, CX, X, Z, Measure, All
circuit_backend = CommandPrinter()

eng=MainEngine(backend=circuit_backend)

qubits = eng.allocate_qureg(3)
All(H) | qubits

H | qubits[1]

CX | (qubits[0], qubits[1])

CX | (qubits[1], qubits[2])

eng.flush(deallocate_qubits=True)

可以看到相应的结果如下：

代码语言：javascript

复制

Allocate | Qureg[0]

H | Qureg[0]

Allocate | Qureg[1]

CX | ( Qureg[0], Qureg[1] )

Deallocate | Qureg[0]

Allocate | Qureg[2]

H | Qureg[2]

CX | ( Qureg[1], Qureg[2] )

Deallocate | Qureg[1]

Deallocate | Qureg[2]

区别于上面的两个例子我们可以发现，这里仅有2个

门而上面的例子中都有3个

门，这就说明在量子编译中两个连续的

门成功的被抵消了。

ProjectQ输出量子线路图

代码语言：javascript

复制

from projectq import MainEngine

from projectq.backends import CircuitDrawer

from projectq.ops import H, CX, X, Z, Measure, All
circuit_backend = CircuitDrawer()

circuit_backend.set_qubit_locations({0: 2, 1: 1, 2:0})

eng=MainEngine(backend=circuit_backend)

qubits = eng.allocate_qureg(3)
All(H) | qubits

CX | (qubits[0], qubits[1])

CX | (qubits[1], qubits[2])

All(Measure) | qubits

eng.flush()
print (circuit_backend.get_latex())

执行输出的是一串完整的LaTex格式代码，可以存储为file_name.tex再进行编译。

代码语言：javascript

复制

\documentclass{standalone}

\usepackage[margin=1in]{geometry}

\usepackage[hang,small,bf]{caption}

\usepackage{tikz}

\usepackage{braket}

\usetikzlibrary{backgrounds,shadows.blur,fit,decorations.pathreplacing,shapes}
\begin{document}

\begin{tikzpicture}[scale=0.8, transform shape]
\tikzstyle{basicshadow}=[blur shadow={shadow blur steps=8, shadow xshift=0.7pt, shadow yshift=-0.7pt, shadow scale=1.02}]\tikzstyle{basic}=[draw,fill=white,basicshadow]

\tikzstyle{operator}=[basic,minimum size=1.5em]

\tikzstyle{phase}=[fill=black,shape=circle,minimum size=0.1cm,inner sep=0pt,outer sep=0pt,draw=black]

\tikzstyle{none}=[inner sep=0pt,outer sep=-.5pt,minimum height=0.5cm+1pt]

\tikzstyle{measure}=[operator,inner sep=0pt,minimum height=0.5cm, minimum width=0.75cm]

\tikzstyle{xstyle}=[circle,basic,minimum height=0.35cm,minimum width=0.35cm,inner sep=-1pt,very thin]

\tikzset{

shadowed/.style={preaction={transform canvas={shift={(0.5pt,-0.5pt)}}, draw=gray, opacity=0.4}},

}

\tikzstyle{swapstyle}=[inner sep=-1pt, outer sep=-1pt, minimum width=0pt]

\tikzstyle{edgestyle}=[very thin]
\node[none] (line0_gate0) at (0.1,-0) {\Ket{0}};

\node[none] (line0_gate1) at (0.5,-0) {};

\node[none,minimum height=0.5cm,outer sep=0] (line0_gate2) at (0.75,-0) {};

\node[none] (line0_gate3) at (1.0,-0) {};

\draw[operator,edgestyle,outer sep=0.5cm] ([yshift=0.25cm]line0_gate1) rectangle ([yshift=-0.25cm]line0_gate3) node[pos=.5] {H};

\draw (line0_gate0) edge[edgestyle] (line0_gate1);

\node[none] (line1_gate0) at (0.1,-1) {\Ket{0}};

\node[none] (line1_gate1) at (0.5,-1) {};

\node[none,minimum height=0.5cm,outer sep=0] (line1_gate2) at (0.75,-1) {};

\node[none] (line1_gate3) at (1.0,-1) {};

\draw[operator,edgestyle,outer sep=0.5cm] ([yshift=0.25cm]line1_gate1) rectangle ([yshift=-0.25cm]line1_gate3) node[pos=.5] {H};

\draw (line1_gate0) edge[edgestyle] (line1_gate1);

\node[none] (line2_gate0) at (0.1,-2) {\Ket{0}};

\node[none] (line2_gate1) at (0.5,-2) {};

\node[none,minimum height=0.5cm,outer sep=0] (line2_gate2) at (0.75,-2) {};

\node[none] (line2_gate3) at (1.0,-2) {};

\draw[operator,edgestyle,outer sep=0.5cm] ([yshift=0.25cm]line2_gate1) rectangle ([yshift=-0.25cm]line2_gate3) node[pos=.5] {H};

\draw (line2_gate0) edge[edgestyle] (line2_gate1);

\node[xstyle] (line1_gate4) at (1.4000000000000001,-1) {};

\draw[edgestyle] (line1_gate4.north)--(line1_gate4.south);

\draw[edgestyle] (line1_gate4.west)--(line1_gate4.east);

\node[phase] (line2_gate4) at (1.4000000000000001,-2) {};

\draw (line2_gate4) edge[edgestyle] (line1_gate4);

\draw (line1_gate3) edge[edgestyle] (line1_gate4);

\draw (line2_gate3) edge[edgestyle] (line2_gate4);

\node[xstyle] (line0_gate4) at (1.9500000000000002,-0) {};

\draw[edgestyle] (line0_gate4.north)--(line0_gate4.south);

\draw[edgestyle] (line0_gate4.west)--(line0_gate4.east);

\node[phase] (line1_gate5) at (1.9500000000000002,-1) {};

\draw (line1_gate5) edge[edgestyle] (line0_gate4);

\draw (line0_gate3) edge[edgestyle] (line0_gate4);

\draw (line1_gate4) edge[edgestyle] (line1_gate5);

\node[measure,edgestyle] (line0_gate5) at (2.6000000000000005,-0) {};

\draw[edgestyle] ([yshift=-0.18cm,xshift=0.07500000000000001cm]line0_gate5.west) to [out=60,in=180] ([yshift=0.035cm]line0_gate5.center) to [out=0, in=120] ([yshift=-0.18cm,xshift=-0.07500000000000001cm]line0_gate5.east);

\draw[edgestyle] ([yshift=-0.18cm]line0_gate5.center) to ([yshift=-0.07500000000000001cm,xshift=-0.18cm]line0_gate5.north east);

\draw (line0_gate4) edge[edgestyle] (line0_gate5);

\node[measure,edgestyle] (line1_gate6) at (2.6000000000000005,-1) {};

\draw[edgestyle] ([yshift=-0.18cm,xshift=0.07500000000000001cm]line1_gate6.west) to [out=60,in=180] ([yshift=0.035cm]line1_gate6.center) to [out=0, in=120] ([yshift=-0.18cm,xshift=-0.07500000000000001cm]line1_gate6.east);

\draw[edgestyle] ([yshift=-0.18cm]line1_gate6.center) to ([yshift=-0.07500000000000001cm,xshift=-0.18cm]line1_gate6.north east);

\draw (line1_gate5) edge[edgestyle] (line1_gate6);

\node[measure,edgestyle] (line2_gate5) at (2.0500000000000003,-2) {};

\draw[edgestyle] ([yshift=-0.18cm,xshift=0.07500000000000001cm]line2_gate5.west) to [out=60,in=180] ([yshift=0.035cm]line2_gate5.center) to [out=0, in=120] ([yshift=-0.18cm,xshift=-0.07500000000000001cm]line2_gate5.east);

\draw[edgestyle] ([yshift=-0.18cm]line2_gate5.center) to ([yshift=-0.07500000000000001cm,xshift=-0.18cm]line2_gate5.north east);

\draw (line2_gate4) edge[edgestyle] (line2_gate5);
\end{tikzpicture}

\end{document}

不过这里推荐另外一种更加方便的做法，避免自己去安装众多的第三方tex包，可以直接使用Overleaf平台来执行tex文件的编译操作，演示效果如下图所示：

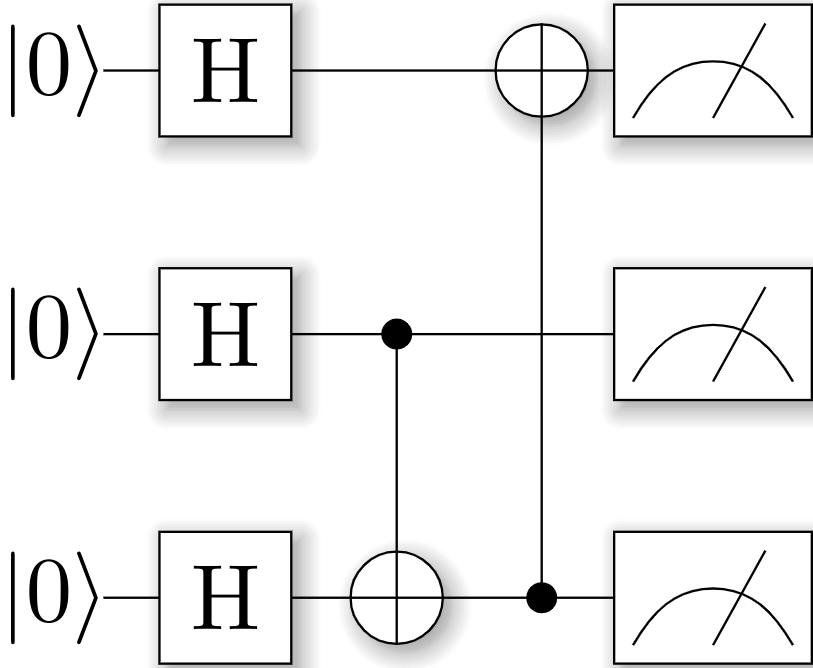
在Overleaf里面会自动的帮我们配置好相关的Latex环境，大大减轻我们自己的工作量。这里的量子线路图绘制时跟比特顺序本身是相关的，比如这里我们尝试切换一种量子比特的映射编号，就会得到不同的线路图(在数学和物理上是等价的)：

代码语言：javascript

复制

from projectq import MainEngine

from projectq.backends import CircuitDrawer

from projectq.ops import H, CX, X, Z, Measure, All
circuit_backend = CircuitDrawer()

circuit_backend.set_qubit_locations({0: 1, 1: 2, 2:0})

eng=MainEngine(backend=circuit_backend)

qubits = eng.allocate_qureg(3)
All(H) | qubits

CX | (qubits[0], qubits[1])

CX | (qubits[1], qubits[2])

All(Measure) | qubits

eng.flush()
print (circuit_backend.get_latex())

生成的latex代码这里就不做展示了，我们可以直接看下编译后输出的量子线路图：

ProjectQ输出资源统计结果

说到量子计算的资源估计，这里面就需要结合实际场景来分析，这是因为即使我们给出了一个非常精妙的线路，但是这个量子线路最终可能也很难真正在量子计算硬件上实现，这是由于不同的硬件体系本身所具备的局限性。这里我们可以考虑在给定量子门集合的条件下的资源估计，我们先还是用给定的量子门集合来编译上述的示例：

代码语言：javascript

复制

from projectq import MainEngine

from projectq.backends import CommandPrinter

from projectq.ops import H, CX, X, Z, Rx, Ry, Rz, Measure, All

from projectq.setups import linear
compiler_engines = linear.get_engine_list(num_qubits=16,

one_qubit_gates=(Rx, Ry, Rz),

two_qubit_gates=(CX, ))

circuit_backend = CommandPrinter()

eng=MainEngine(backend=circuit_backend, engine_list=compiler_engines)

qubits = eng.allocate_qureg(3)
All(H) | qubits

CX | (qubits[0], qubits[1])

CX | (qubits[1], qubits[2])

eng.flush(deallocate_qubits=True)

这里我们使用的是

{R_x,R_y,R_z,CX}

这个组合，而并不包含上述用例中使用到的

门，这里我们可以看下输出结果(其实就是用

R_x

和

R_y

的组合来构建一个

门)：

代码语言：javascript

复制

Allocate | Qureg[1]

Ry(1.570796326795) | Qureg[1]

Rx(9.424777960769) | Qureg[1]

Allocate | Qureg[0]

Ry(1.570796326795) | Qureg[0]

Rx(9.424777960769) | Qureg[0]

CX | ( Qureg[0], Qureg[1] )

Allocate | Qureg[2]

Ry(1.570796326795) | Qureg[2]

Rx(9.424777960769) | Qureg[2]

CX | ( Qureg[1], Qureg[2] )

Deallocate | Qureg[1]

Deallocate | Qureg[2]

Deallocate | Qureg[0]

针对于这种场景，我们切换下后端就可以实现量子计算资源的统计：

代码语言：javascript

复制

from projectq import MainEngine

from projectq.backends import ResourceCounter

from projectq.ops import H, CX, X, Z, Rx, Ry, Rz, Measure, All

from projectq.setups import linear
compiler_engines = linear.get_engine_list(num_qubits=16,

one_qubit_gates=(Rx, Ry, Rz),

two_qubit_gates=(CX, ))

circuit_backend = ResourceCounter()

eng=MainEngine(backend=circuit_backend, engine_list=compiler_engines)

qubits = eng.allocate_qureg(3)
All(H) | qubits

CX | (qubits[0], qubits[1])

CX | (qubits[1], qubits[2])

All(Measure) | qubits

eng.flush(deallocate_qubits=True)
print (circuit_backend)

这个程序实际上就是统计上一个示例代码中输出的量子线路的门的数量，对应输出结果为：

代码语言：javascript

复制

Gate class counts:

AllocateQubitGate : 3

CXGate : 2

DeallocateQubitGate : 3

MeasureGate : 3

Rx : 3

Ry : 3
Gate counts:

Allocate : 3

CX : 2

Deallocate : 3

Measure : 3

Rx(9.424777960769) : 3

Ry(1.570796326795) : 3
Max. width (number of qubits) : 3.

这里我们可以看到，统计中的

R_x,R_y,CX

的门的数量与上面输出的结果是保持一致的，那么我们的示例到这里就成功完成演示。

总结概要

这篇文章中，我们通过介绍开源量子计算编程框架ProjectQ的一些常规使用方法，来讲解了如何使用程序来编译和生成量子线路，以及将该量子线路作为字符串或者Latex格式代码输出，这同时也使得我们可以通过输出结果来统计量子计算的资源，以用于预测在大规模场景下所需要的大致的量子比特数以及门操作数量(或用量子线路深度来衡量)的量级。这种编译的手段和资源估计的方法，在工程和科学研究上都有较大的意义。

版权声明

本文首发链接为：https://cloud.tencent.com/developer/article/1827372

作者ID：DechinPhy

更多原著文章请参考：https://www.cnblogs.com/dechinphy/

参考链接

https://github.com/ProjectQ-Framework/ProjectQ