本代码可以用来快速计算四周固定的圆板在均布载荷下大挠度弯曲的位移。
代码语言:javascript
复制
from matplotlib import pyplot as plt
import numpy as np
class RoundPlate(object):
def init(self, E: float, nu: float, a: float, t: float):
"""弹性模量,泊松比,半径,板厚"""
self.E = E # 弹性模量
self.nu = nu # 泊松比
self.D = E * t3 / (12.0 * (1-nu2)) # 板的抗弯刚度
self.g_nu = (-2791.0nunu + 4250.0*nu + 7505.0) / 17640.0 # 仅与泊松比相关的系数
self.a = a # 圆板的半径
self.t = t # 板的厚度
def w0_linear(self, q: float) -> float: #
"""求线性条件下的板最大位移(圆心处位移),q 为均布载荷(压强)"""
return (self.a**4) * q / 64.0 / self.D
def f_w0(self, w0: float, q: float) -> float:
"""求非线性条件下的板最大位移w0(圆心处位移)的方程 f_w0(w0)=0"""
return w0 + self.g_nu/self.t**2 * w0**3 - self.w0_linear(q)
def d_f_w0(self, w0: float) -> float:
"""d f_w0(w0)/d(w0), f_w0的一阶导数,for牛顿迭代法"""
return 3.0 * self.g_nu/self.t**2 * w0*w0 + 1.0
def solve(self, q: float, error: float = 1e-10) -> float:
"""牛顿迭代法求解一元方程。q 为均布载荷(压强),error 为求解精度"""
x = self.w0_linear(q) # 用线性条件下的板最大位移 做为迭代的初值
i = 0
while True:
delta_x = self.f_w0(x, q) / self.d_f_w0(x)
x = x - delta_x
if delta_x < error:
break
i += 1
# print(f"// {i} 次迭代后收敛 //")
return x
def w(self, rho: float, q: float, error: float = 1e-10):
"""计算板中面任一点的位移"""
w0 = self.solve(q, error) # 中面中心点位移
return w0 * (1 - (rho / self.a)**2)**2
if name == "main":
# 模型输入
E = 200e9 # 弹性模量
nu = 0.30 # 泊松比
a = 1.0e-3 # 圆板的半径
t = 1.0e-6 # 板的厚度
rb = RoundPlate(E, nu, a, t)
q0 = 2.0 # 分布载荷
print(f"抗弯刚度 D = {rb.D}")
print(f"线性条件下的板最大位移 w0_L = {rb.w0_linear(q0)}")
print(f"非线性条件下板最大位移 w0 = {rb.solve(q0)}")
Q = np.linspace(0, 2, 101)
# print(Q)
W0_L = np.frompyfunc(rb.w0_linear, 1, 1)(Q)
# print(W0_L)
W0 = np.frompyfunc(rb.solve, 2, 1)(Q, 1e-10)
# print(W0)
plt.title("四周固定的圆板在均布载荷下大挠度弯曲最大位移计算")
plt.plot(Q, W0_L, c='b', linestyle="--", label="线性条件下最大位移")
plt.scatter(Q, W0_L)
plt.plot(Q, W0, c='g', linestyle="-", label="非线性条件下最大位移")
plt.scatter(Q, W0)
plt.xlabel("均布载荷q")
plt.ylabel("最大位移(中心位移)")
plt.legend(loc="lower right")
plt.show()
print(f"中心点位移:{rb.w(0,2)}")
print(f"边缘位移:{rb.w(rb.a, 2)}")
print(Q.max())
R = np.linspace(-rb.a, rb.a, 101)
W = -np.frompyfunc(rb.w, 3, 1)(np.abs(R), Q.max(), 1e-10)
plt.title("四周固定的圆板在均布载荷下大挠度弯曲 挠曲面")
plt.plot(R, W, c='b')
plt.xlabel("坐标 r")
plt.ylabel("垂向位移")
plt.show()</code></pre></div></div><p> <code>程序绘图:</code></p><figure class=""><div class="rno-markdown-img-url" style="text-align:center"><div class="rno-markdown-img-url-inner" style="width:100%"><div style="width:100%"><img src="https://cdn.static.attains.cn/app/developer-bbs/upload/1723364288623799732.png" /></div></div></div></figure><figure class=""><div class="rno-markdown-img-url" style="text-align:center"><div class="rno-markdown-img-url-inner" style="width:100%"><div style="width:100%"><img src="https://cdn.static.attains.cn/app/developer-bbs/upload/1723364289026752757.png" /></div></div></div></figure><p>程序输出:
代码语言:javascript复制抗弯刚度 D = 1.831501831501831e-08
线性条件下的板最大位移 w0_L = 1.7062500000000006e-06
非线性条件下板最大位移 w0 = 1.086361827668184e-06
中心点位移:1.086361827668184e-06
边缘位移:0.0
下面是专业有限元软件的计算结果(1000x5 个单元的轴对称模型):
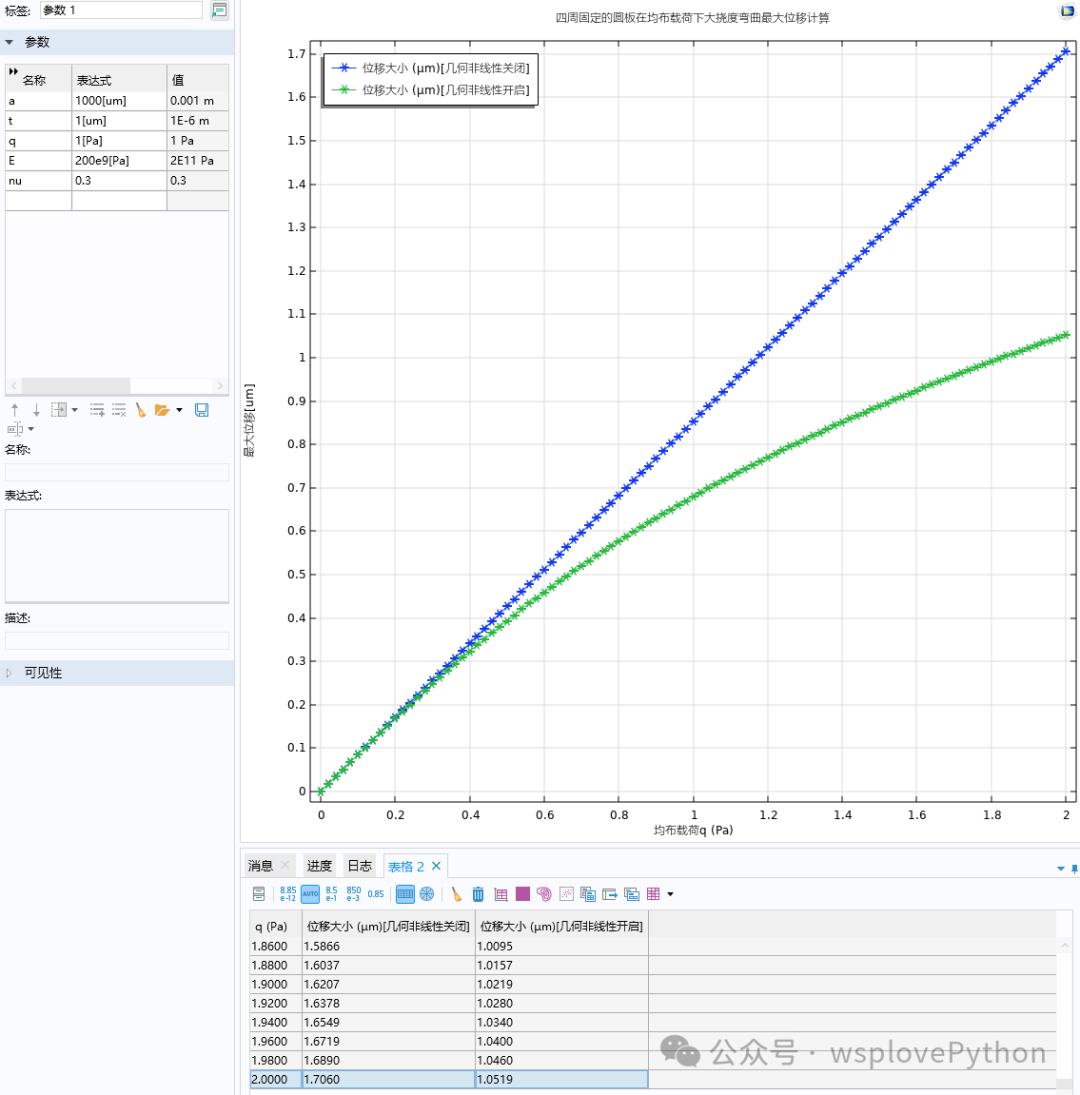
二者只相差 3%,精度很不错。
下面是w0 方程的推导过程,用的是能量法+变分法, 参考书是弹性力学教材(该教材上只有泊松比为0.3时的挠曲线方程):


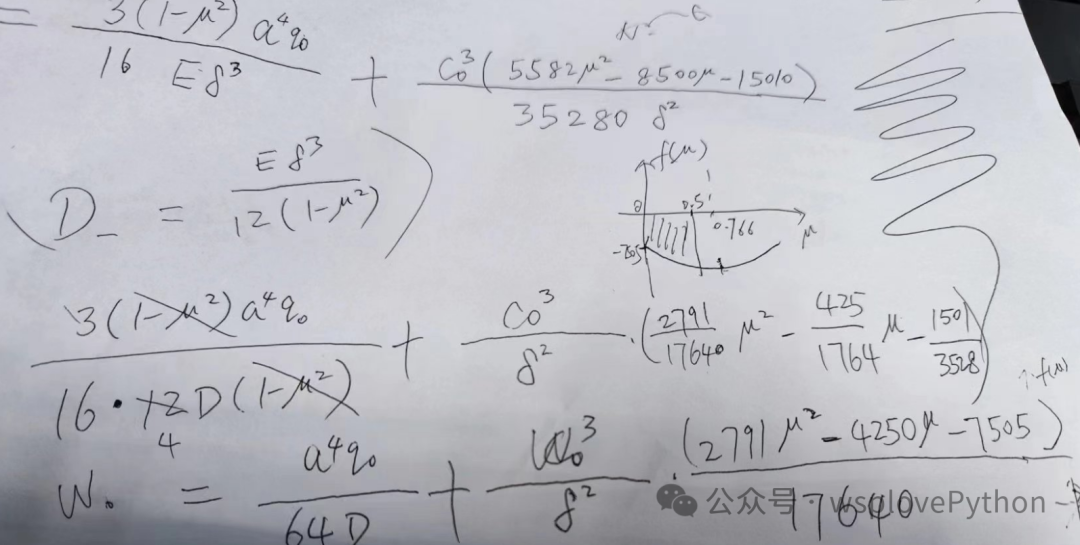
注意,推导公式里的delta 是板厚,rho是离中心点的距离, C0是W0。