新智元编译
来源:singularityhub
作者:大明
【新智元导读】摩尔定律不断给人这种感觉:就是在此时此刻,我们正处于人工智能行业独一无二的大变革时期。然而,只要计算力的增长继续遵循指数级的价格-性能曲线,那么未来的每一代人回过头来看时,过去的时代都会是几乎没有进步的时代。
现在我们中的大部分人都很熟悉摩尔定律,这个著名的定律指出,计算力的发展遵循指数曲线,每18个月性价比(即单位成本下的计算速度)翻一倍。不过,在将摩尔定律应用在自己的商业策略中的时候,即便是眼光最长远的人也难免遭遇巨大的“AI盲点”。
我曾经与很多成功的、策略大师级的杰出商人接触过,他们都善于在业内不起眼的角落里发现商机,但却把握不住摩尔定律所说的“指数发展曲线”的真正意义。藉由这条曲线获利的行业有很多,但有一个技术领域尤其获益颇丰,即人工智能。
人们无法把握人工智能的发展究竟有多快的原因之一是,它的发展轨迹过于简单,甚至有些可笑:从实用性的角度来说,要想在幻灯片或图表这种有限空间上描绘出指数曲线的陡峭轨迹几乎是不可能的。形象化地描绘出这一曲线的早期图像是可行的,不过随着曲线迅速变得越来越陡峭,相关数字会迅速增大,让绘图变得越来越麻烦。
为了解决这一视觉空间不足的问题,我们可以使用对数刻度作为数学工具,将指数曲线压扁,以便在较小的空间内呈现。
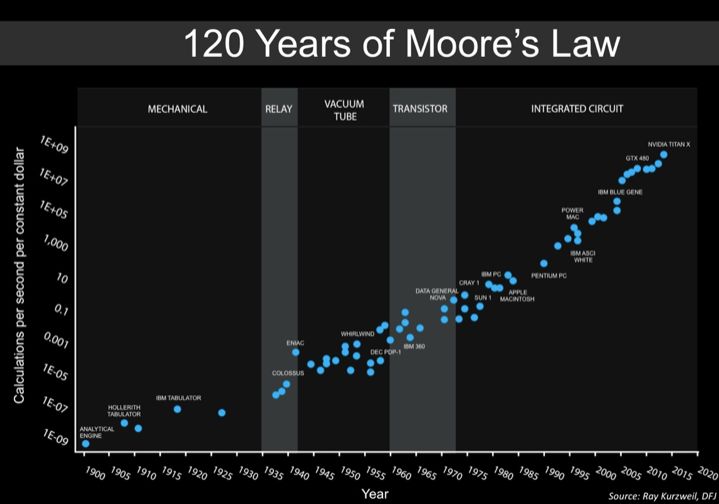
遗憾的是,广泛应用的对数刻度也会导致另一个问题。这个工具的原理是:竖直方向上Y坐标轴上的刻度不在按照线性增加,而是乘以一个倍数,比如100倍。经典的摩尔定律图(如下图)一般都会使用对数刻度来刻画过去120年来计算力成本的指数级发展(Y轴单位为每1美元能买到的每秒计算次数),图表的涵盖范围从20世纪初的机械设备,一直到今天性能强大的硅基GPU。

图1:以对数刻度绘制的计算成本的指数级发展。
现在,对数刻度图已经成为一种很有价值的工具,节省空间,便于速记。实际上,对于任何随时间陡峭而迅速上升的曲线,都可以利用对数刻度进行方便处理。
不过,对数刻度的应用也伴随着一个潜在的巨大代价:它会欺骗你的眼睛。
对数刻度会在数学上将巨大的数字压缩,使指数曲线呈现为线性。由于该工具将不受控制的指数增长曲线压缩成线性,让人们很容易对未来计算能力增长的速度产生舒适感,甚至滋生自满情绪。
我们的逻辑大脑能够理解对数图,但是我们在潜意识中却看到了一条线性的曲线。
那么,有什么有效的方法能够消除对数图表带来的“战略性近视”问题呢?重新回归原来的线性刻度可能会解决一部分问题。
如下图2所示,我利用数据拟合一条指数曲线,然后在Y轴使用线性刻度绘图。同样地,Y轴同样表示1美元能够买到的运算速度(单位为Gflop),X轴表示时间。不过在图2中,Y轴上的每个刻度对应的计算力增量仅为1Gflop(而不是图1中的100Gflop)。flop一词是指每秒钟的浮点操作数,是衡量计算力的标准量度。
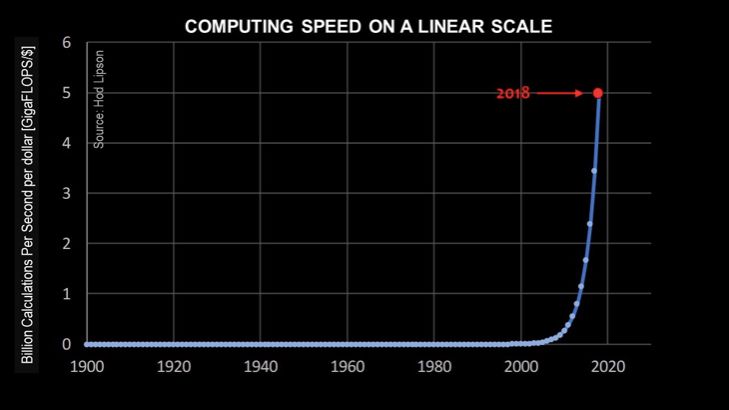
图2:以线性刻度绘制的摩尔定律图表
图2所示为实际的、真正反映摩尔定律的指数曲线。从这张表中,我们可以很容易理解单位价格计算性能在过去十年中的迅速发展。不过,这张图中存在一些严重错误,从表中来看,似乎在整个20世纪,计算机的成本和性能根本没有提高,而这很明显是错误的。
图2表明,用线性刻度呈现摩尔定律随时间的变化也可能会有问题。这种方式会让过去时间段的曲线看上去很平,好像一直完全没有进步,直到最近才有所发展。此外,这种线性刻度的图表也会导致人们得出错误的结论:觉得当前的有利时间点就代表了一段独一无二的“几乎飞跃式”的技术进步。
这一点让我想到由图表引起的“AI盲区”的又一个主要原因:线性刻度图表富有欺骗性,让人们以为自己生活在发展变革的高峰期。
现代生活造成的“近视”
让我们再来看图2。如果从2018年的情况开始看,那么整个20世纪中每十年一次的性价比翻倍,在曲线上看就是平的,显得几乎无足轻重。一个人看了图2,可能会对自己说:“多亏我活到了现在。我还记得2009年时,我以为我的iPhone就算快的了,我当时都不知道它有多慢!现在我总算赶上令人激动的飞跃时刻了!”
但事实并非如此。这种垂直式的“转变点”实际上并不存在。
每条指数曲线都是自相似的,也就是说,未来的曲线形状和过去的曲线形状是一样的。在下方的图3中再次采用线性刻度绘制了摩尔定律的指数曲线,但不同的是,图3是以2028年的视角绘制的。这条曲线假设,我们在过去100年中的经历的技术进步还会在未来至少10年内继续。该图表明,在2028年,1美元将能够买到大约200Gflop的计算力。
不过,图3也呈现出一些分析上的困境。
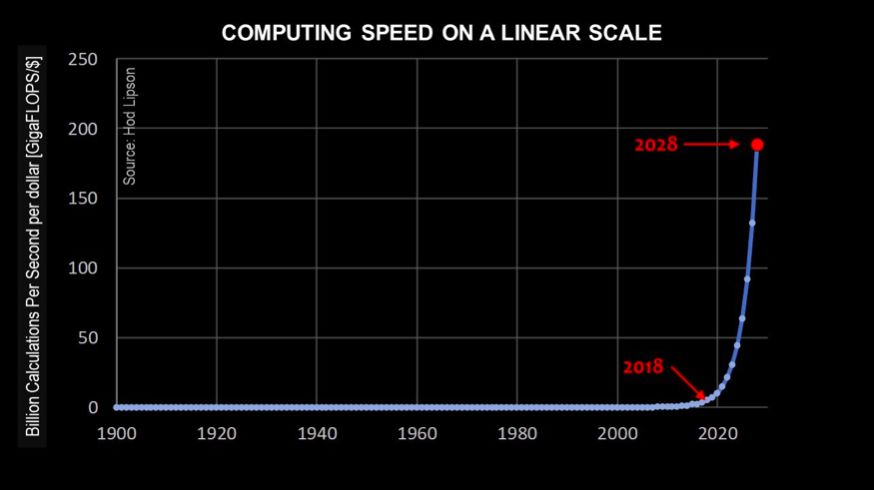
图3 以线性刻度绘制的摩尔定律曲线(2028年视角)
在图中仔细观察今天(2018年)的计算力,如果从2028年生活和工作的人所处的优势点来看,看上去似乎在21世纪初期,计算力似乎也完全没有任何进步。就好像2018年我们使用的计算设备也就比上世纪50年代的设备性能强一点点而已。观察者也可以得出结论,认为当前年份(2028年)为摩尔定律的顶点,即计算力的进步最终一飞冲天的时刻。
每年我都会对图3进行重绘,只改变时间跨度。重绘后的曲线形状几乎完全不变,只有Y轴的刻度会有改变。可以看到,除了Y轴的刻度有所区别之外,图2和图3的形状几乎完全相同。从每张图上的未来的时间点看,过去时间点的曲线都是平的。嗯,这种误解可能会导致有缺陷的商业策略,尤其是在人工智能领域。
这意味着什么?
对于人们而言,指数级的变化率往往很难理解,也很难看明白。指数曲线的特殊之处在于,它的每个点在数学上都是自相似的。也就是说,这种不断爬升的曲线没有平坦部分,没有上升部分,也不存在很多商人所说的“肘部”和“曲棍球棒”弯曲部分。如果你对过去或未来某时间段的曲线放大观察,你会发现它们的形状完全相同。
摩尔定律不断给人这种感觉,就是在此时此刻,我们正处于人工智能行业(以及其他与摩尔定律有关的行业)独一无二的大变革时期。然而,只要计算力的增长继续遵循指数级的价格-性能曲线,那么未来的每一代人回过头来看时,过去的时代都会是几乎没有进步的时代。此话反过来也是成立的,即当前的一代人展望10年后的未来,同样想象不到人将会取得多大的进步。
所以,如果有人规划计算力呈指数增长的未来,那么现在的挑战在于克服自己的大脑对该曲线的有缺陷的理解方式。这听起来很难,你需要记住上面的三幅图表(视觉一致性很高的对数刻度图,以及富有欺骗性、但看起来很过瘾的线性刻度图),真正体会指数级增长的力量。因为过去看上去总是平的,而未来看上去总是一飞冲天。
原文地址:
https://singularityhub.com/2018/07/15/why-most-of-us-fail-to-grasp-coming-exponential-gains-in-ai/#sm.000007jycsxmx6cvrv703hbej2cjz