Compute the Optimal Policy & the Optimal Value 计算最佳策略和计算最佳价值

发布于

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/Solo95/article/details/102500566

MDP Control

在这节内容里我们不讨论如何学习策略，我们仅仅探讨计算最佳策略。 计算最佳策略和计算最佳价值都属于MDP Control。

  • 计算最佳策略 π∗(s)=argmaxπVπ(s)\pi^*(s)=\mathop{argmax}\limits_{\pi} V^\pi(s)π∗(s)=πargmax​Vπ(s)
  • 存在一个独一无二的最优价值函数
  • 在一个有限horizon内MDP的最优策略是确定的

最后一条是一个非常好的原因，能够解答为什么我们仅仅关注确定性策略就已经足够解决问题。

火星小车可以移动。

在这里插入图片描述

那么一共有多少个确定性策略?

272^727 计算公式∣A∣∣s∣|A|^{|s|}∣A∣∣s∣

MDP的最优策略永远是独一无二的吗？

不是的。因为可能存在两个不同的动作由相同的价值函数。

在上面这个例子中，最优价值函数是独一无二的，虽然可以有多个最优策略，但这些策略计算出来的价值的最大值是一样的。
同时，我们假定在所有的状态下所有的动作都是能够进行的。虽然在现实世界，这可能并不成立。在很多实际例子中，一些动作是指定在某些状态下才能执行的。

总结下来：

  • 计算最佳策略
    π∗(s)=argmaxπVπ(s)\pi^*(s)=\mathop{argmax}\limits_{\pi} V^\pi(s)π∗(s)=πargmax​Vπ(s)
  • 存在一个独一无二的最优价值函数
  • 在一个有限horizon内MDP的最佳策略(哪怕agent永远在行动)
    • 确定的(Deterministic)
    • 固定不动的(Stationary, does not depend on tims step)
    • 独一无二的？不需要非得是独一无二的，可能有多个状态-动作对拥有相同的最佳价值。

策略搜索

  • 一个选项是使用搜索去计算最佳策略
  • 确定性策略的数量是∣A∣∣S∣|A|^{|S|}∣A∣∣S∣
  • 策略迭代通常比暴力枚举更高效
MDP Policy Iteration(PI)

(下面是是一个算法，Markdown代码模式无法输入公式，所以写成这样)

  • Set i = 0
  • Initialize π0(s)\pi_0(s)π0​(s) randomly for all states s
  • While i==0i == 0i==0 or ∥πi−πi−1∥>0|\pi_i-\pi_{i-1}|>0∥πi​−πi−1​∥>0 (L1L_1L1​-norm, measures if the policy changed for any state):
    • Vπi←MDPV^{\pi_i} \leftarrow MDPVπi​←MDP V function policy evaluation of πi\pi_iπi​
    • πi+1←\pi_{i+1} \leftarrowπi+1​← Policy improvement
    • i = i + 1

New Dedinition: State-Action Value Q

为了定义我们如何改进一个策略，我们定义状态-动作价值 Q。

在之前的叙述中，我们使用如下notation描述状态-动作价值: Vπ(s)V^\pi(s)Vπ(s) 即，采用策略π\piπ时在状态s下的动作价值。这里我们定义新的概念，同时也定义了Q函数。

一个策略的状态-动作价值是： Qπ(s,a)=R(s,a)+γ∑s′∈SP(s′∣s,a)Vπ(s′)Q^\pi(s, a) = R(s, a) + \gamma \sum_{s' \in S}P(s'|s,a)V^\pi(s')Qπ(s,a)=R(s,a)+γ∑s′∈S​P(s′∣s,a)Vπ(s′)

它的直观理解是，我先采取动作a，然后再遵循策略π\piπ。

Policy Imporvement
  • Compute state-action value of a policy πi\pi_iπi​
    • For s in S and a in A:
      • Qπi(s,a)=R(s,a)+γ∑s′∈SP(s′∣s,a)Vπi(s′)Q^{\pi_i}(s, a) = R(s, a) + \gamma \sum_{s' \in S}P(s'|s,a)V^{\pi_i}(s')Qπi​(s,a)=R(s,a)+γ∑s′∈S​P(s′∣s,a)Vπi​(s′)
  • Compute new policy πi+1\pi_{i+1}πi+1​, for all s∈Ss\in Ss∈S
    • πi+1(s)=argmaxaQπi(s,a)\pi_{i+1}(s) =\mathop{argmax}\limits_{a}Q^{\pi_i}(s,a)πi+1​(s)=aargmax​Qπi​(s,a) ∀s inS\forall s \ in S∀s inS

上面的等式中，maxaQπi(s,a)≥Qπi(s,πi(s))\mathop{max}\limits_{a} Q^{\pi_i}(s, a)\geq Q^{\pi_i}(s, \pi_i(s))amax​Qπi​(s,a)≥Qπi​(s,πi​(s))，也就是说，agent要么采取了策略指定的动作，要么采取了经由argmaxargmaxargmax Q function计算得到的更好的动作，从而产生了新的策略。

如果采用梯度下降的策略迭代方法，跟其他深度学习方法一样，会有局部最优值的问题，但是目前的情景下不会遇到这样的情况。

更进一步理解优化(改进)步骤：

在这里插入图片描述
  • 假设我们在一个action采取了计算的得到的πi+1(s)\pi_{i+1}(s)πi+1​(s)，然后再一直遵循旧的πi\pi_iπi​。
    • 我们的回报期望总值至少和从头到尾遵循πi\pi_iπi​一样
  • 但是奇怪的是，新提出的策略将会一直遵循πi+1\pi_{i+1}πi+1​

改进步骤将会单调递增地改进策略价值。

为什么？

Momotonic Improvement in Policy Value

定义(Definition)： Vπ1≥Vπ2:Vπ1(s)≥Vπ2(s),∀s∈SV^{\pi_1}\geq V^{\pi_2}: V^{\pi_1}(s) \geq V^{\pi_2}(s), \forall s \in SVπ1​≥Vπ2​:Vπ1​(s)≥Vπ2​(s),∀s∈S

命题(Proposition): Vπi+1≥VπiV^{\pi_{i+1}}\geq V^{\pi_i}Vπi+1​≥Vπi​，在πi\pi_iπi​是次优的条件下，这个不等式严格成立，其中πi+1\pi_{i+1}πi+1​是我们在πi\pi_iπi​上进行策略优化得到的。

证明过程如下：

在这里插入图片描述

证明思路总结如下：不等式右边按定义展开，然后再构造另一个不等式，这个不等式的右边可以展开成一个迭代过程，刚好等于Vπi+1(s)V^{\pi_{i+1}(s)}Vπi+1​(s)。

回顾前述内容策略优化的过程：

在这里插入图片描述

如果策略不发生改变了，策略有再次发生改变的可能性吗？

没有。πi+1=πi\pi_{i+1}=\pi_{i}πi+1​=πi​

在这里插入图片描述

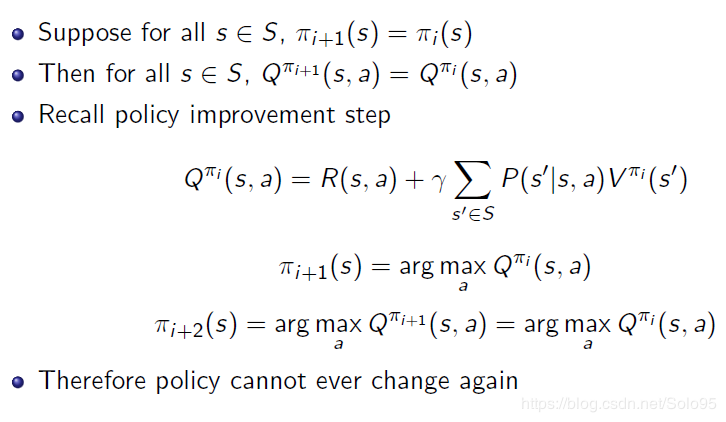
有策略迭代次数的最大值吗？

有，如前面提到的∥A∥∥S∥\|A\|^{\|S\|}∥A∥∥S∥

博主在学习TD Learning之后回来补充一点：这其实就是Q-Learining。

MDP: Computing Optimal Policy and Optimal Value

  • 策略迭代计算最优价值和最优策略
  • 价值迭代是另外一种技术：
    • 思想：在本轮(this episode)中，从状态s开始还剩下k步，这维持了一个最优值。
    • 迭代地以类似方式思考后面的轮次。

这和策略地带的不同之处在于： 在策略迭代中，你总是都有一个策略，并且你知道它的价值，只是这个策略可能不是很好。 在价值迭代中，你总是知道策略中的最优价值，但是你仅仅需要执行k步才能得到。

Bellman Equation and Bellman Backup Operators

一个策略的价值函数必须满足Bellman Equation: Vπ(s)=Rπ(s)+γ∑s′∈SPπ(s′∣s)Vπ(s′)V^\pi(s)=R^\pi(s) + \gamma \sum_{s' \in S}P^\pi(s'|s)V^\pi(s')Vπ(s)=Rπ(s)+γs′∈S∑​Pπ(s′∣s)Vπ(s′)

  • Bellman backup operator
    • 应用于一个价值函数
    • 返回一个新的价值函数
    • 尽可能的提升价值 BV(s)=maxaR(s,a)+γ∑s∈Sp(s′∣s,a)V(s′)BV(s) = \mathop{max}\limits_{a}R(s,a)+\gamma\sum_{s \in S}p(s'|s,a)V(s')BV(s)=amax​R(s,a)+γs∈S∑​p(s′∣s,a)V(s′)

有时我们会使用BV来表示Bellman Operator，意思是，在每次迭代，你取就的V值代入上式的右边计算新的V值。

Value Iteration (VI)

算法表示如下：

  • Set k = 1
  • Initialize V0(s)=0V_0(s)=0V0​(s)=0 for all states s
  • Loop until [finite horizon, convergence]:
    • For each state s
      • Vk+1(s)=maxaR(s,a)+γ∑s′∈SP(s′∣s,a)Vk(s′)V_{k+1}(s) = \mathop{max}\limits_{a}R(s,a)+\gamma\sum_{s' \in S}P(s'|s,a)V_k(s')Vk+1​(s)=amax​R(s,a)+γs′∈S∑​P(s′∣s,a)Vk​(s′)
    • View as Bellman backup on value function Vk+1=BVkV_{k+1} = BV_{k}Vk+1​=BVk​ πk+1=argmaxaR(s,a)+γ∑s′∈SP(s′∣s,a)Vk(s′)\pi_{k+1}=\mathop{argmax}\limits_{a}R(s,a) + \gamma\sum_{s' \in S}P(s' | s,a)V_k(s')πk+1​=aargmax​R(s,a)+γ∑s′∈S​P(s′∣s,a)Vk​(s′)

初始化为零时有意义的，因为相当于第一次迭代的时候最优值是一个动作的即时回报，然后把它备份，进行下一次迭代，如如此往复。

Policy Iteration as Bellman Operations

一个特定策略的Bellman backup operator BπB^\piBπ被定义为： BπV(s)=Rπ(s)+γ∑s′∈SPπ(s′∣s)V(s)B^\pi V(s) = R^\pi(s)+\gamma\sum_{s' \in S}P^\pi(s'|s)V(s)BπV(s)=Rπ(s)+γs′∈S∑​Pπ(s′∣s)V(s)

策略迭代等同于计算BπB^\piBπ的不动点。

为了进行策略迭代，重复应用operator直到V停止变化。 Vπ=BπBπ...BπVV^\pi=B^\pi B^\pi...B^\pi VVπ=BπBπ...BπV

所以你可以通过固定策略来初始化Bellman operator。

Policy Iteration as Bellman Operation

一个特定策略的Bellman backup operator BπB^\piBπ被定义为： BπV(s)=Rπ(s)+γ∑s′∈SPπ(s′∣s)V(s)B^\pi V(s) = R^\pi(s)+\gamma\sum_{s' \in S}P^\pi(s'|s)V(s)BπV(s)=Rπ(s)+γs′∈S∑​Pπ(s′∣s)V(s)

为了进行策略优化： πk+1(s)=argmaxaR(s,a)+γ∑s′∈SP(s′∣s,a)Vπk(s′)\pi_{k+1}(s)=\mathop{argmax}\limits_{a}R(s,a) + \gamma\sum_{s' \in S}P(s'|s, a) V^{\pi_k}(s')πk+1​(s)=aargmax​R(s,a)+γs′∈S∑​P(s′∣s,a)Vπk​(s′)

Going back to value Iteration(VI)

算法表示如下：

  • Set k = 1
  • Initialize V0(s)=0V_0(s)=0V0​(s)=0 for all states s
  • Loop until [finite horizon, convergence]:
    • For each state s
      • Vk+1(s)=maxaR(s,a)+γ∑s′∈SP(s′∣s,a)Vk(s′)V_{k+1}(s) = \mathop{max}\limits_{a}R(s,a)+\gamma\sum_{s' \in S}P(s'|s,a)V_k(s')Vk+1​(s)=amax​R(s,a)+γs′∈S∑​P(s′∣s,a)Vk​(s′)
    • Equivalently, in Bellman backup notation
      • Vk+1=BVkV_{k+1}=BV_{k}Vk+1​=BVk​

To extract optimal policy if can act for k+1 more steps, π(s)=argmaxR(s,a)+γ∑s′∈SP(s′∣s,a)Vk+1(s′)\pi(s)=\mathop{argmax}R(s,a)+\gamma\sum_{s' \in S}P(s'|s,a)V_{k+1}(s')π(s)=argmaxR(s,a)+γs′∈S∑​P(s′∣s,a)Vk+1​(s′)

Contration Operator

补充一点缩减(Contration)方面的知识。

  • 定义O是一个操作符，并且∣X∣|X|∣X∣表示x的任何形式的norm
  • 如果∣OV−OV′∣≤∣V−V′∣|OV-OV'|\leq |V-V'|∣OV−OV′∣≤∣V−V′∣，那么O就是一个缩减操作符
Will Value Iteration Converge？

Bellman backup 也是一个缩减操作符。

是的，如果折扣因子γ<1\gamma < 1γ<1，整个过程会以1的概率结束在一个终止状态。

Bellman backup在折扣因子γ<1\gamma < 1γ<1时会缩减。

如果把Ballman backup应用到两个不同的价值函数，两个函数的距离在应用Bellman Equation后会减小。

证明如下，有兴趣的话你可以看看。

在这里插入图片描述

Value Iteration for Finite Horizon

Vk=V_k=Vk​=optimal value if making k more decisions πk=\pi_k=πk​=optimal policy if making k more decisions

  • Initialize V0(s)=0V_0(s)=0V0​(s)=0 for all state s
  • For k=1 : H
    • For each state s Vk+1(s)=maxaR(s,a)+γ∑s′∈SP(s′∣s,a)Vk(s)V_k+1(s)=\mathop{max}\limits_{a}R(s,a)+\gamma\sum_{s' \in S}P(s'|s,a)V_k(s)Vk​+1(s)=amax​R(s,a)+γ∑s′∈S​P(s′∣s,a)Vk​(s) πk+1(s)=argmaxaR(s,a)+γ∑s′∈SP(s′∣s)Vk(s′)\pi_{k+1}(s)=\mathop{argmax}\limits_{a}R(s,a)+\gamma\sum_{s' \in S}P(s'|s)V_k(s')πk+1​(s)=aargmax​R(s,a)+γ∑s′∈S​P(s′∣s)Vk​(s′)

这个算法跟之前讲过的一样，只是限定了迭代到H次，即horizon大小。

在这里插入图片描述

注意，这里说最优策略不是固定的(独立于时间步)，是在迭代求最优价值的情境下，跟博文开头的最优策略不在一个情境下。

Value vs Policy Iteration

  • 价值迭代
    • 计算的是horizon为k时的最优价值
      • 注意这点可以被用来计算最优策略
  • 策略迭代
    • 计算有限horizon内策略的价值
    • 用于选择另外的更好的策略
    • 策略迭代跟RL里一个非常流行的方法策略梯度关系非常紧密
#backup#iteration#policy#state#sum