通过投影统计计算物体朝向

图像处理中会遇到需要计算物体朝向的情况，前文使用转动惯量计算了物体朝向，本文换一种思路，使用投影统计计算朝向。

问题描述

• 对于一幅二值图像，需要求解图像的朝向

解决思路

• 物体上的每个点可以向某个方向投影，完成投影后每个点变为一维数据

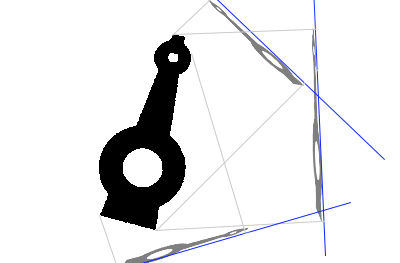
• 直觉上，与真正朝向垂直方向的投影的一维数据，的方差是最小的
• 按照这个思路，求解二值图物体朝向

计算方法

• 图中非零的点有 N 个，坐标为 (x_i, y_i), 0 <i<N

\textbf{x}=[x_1,x_2, …,x_N]^T, \textbf{y}=[y_1,y_2, …,y_N]^T

• 合并为维度 N \times 2 的矩阵 \textbf{M} = [\textbf{x}, \textbf{y}]，
• 给定一条直线，直线过点 (x_t, y_t)，直线的法向量 \textbf{v} = [a, b]^T，该法向量为单位向量，有：

a^ 2 + b ^2=1

• 则直线可表示为：

[x-x_t,y-y_t]\textbf{v} = 0

• 二值图上的点 (x,y) 到直线的有向距离为： 点到(x_t, y_t) 的向量到直线法向量 \textbf{v} 的投影:

d =[x-x_t,y-y_t]\textbf{v}

• 所有点的有向距离组成向量：

\begin{array}{c} \textbf{d} &= [\textbf{M}-[x_t,y_t]]\textbf{v}\ &= \textbf{M}\textbf{v}- [x_t,y_t]\textbf{v} \end{array}

• 设 [x_t,y_t]\textbf{v} 为常数 c，有：

d =[x,y]\textbf{v}-c，\textbf{d} = \textbf{M}\textbf{v}- c

• 我们的目标是找到所有点的有向距离组成的样本集合的方差统计量最小，有向距离的均值为：

\overline{d} =\frac{1}{N} \sum\textbf{M}\textbf{v}- c

• 有向距离的方差可表示为：

\begin{array}{c} Var&=&\frac{1}{N} \sum_{i=1}^N (d_i-\overline{d})^2\\ &=&\frac{1}{N} \sum_{i=1}^N ([x_i,y_i]\textbf{v}-\frac{1}{N} \sum\textbf{M}\textbf{v})^2\\ &=&\frac{1}{N} \sum_{i=1}^N ([x_i-\overline{x},y_i-\overline{y}]\textbf{v})^2 \end{array}

• 可见二值图到直线的有向距离的方差与直线的偏置无关，仅与法向量有关，设 \textbf{M}’=\textbf{M}-[\overline{x}, \overline{y}]，有：

\begin{array}{c} Var&=&\frac{1}{N} \sum_{i=1}^N ([x_i-\overline{x},y_i-\overline{y}]\textbf{v})^2\\ &=&\frac{1}{N} (\textbf{M}’\textbf{v})^T(\textbf{M}’\textbf{v})\\ &=& \frac{1}{N} \textbf{v}^T\textbf{M}’^T\textbf{M}’\textbf{v} \end{array}

• 可以看做 Var 是关于 \textbf{v} 的二次型，系数矩阵为 \frac{1}{N}\textbf{M}’^T\textbf{M}’
• 我们需要该方差最小，则对 \textbf{v} 求导，取值为零

\begin{array}{c} \frac{{\partial Var}}{{\partial {\bf{v}}}} = \frac{2}{N}\textbf{M}’^T\textbf{M}’\bf{v}= 0\\ \textbf{M}’^T\textbf{M}’\bf{v}= 0 \end{array}

参考资料

• https://www.zywvvd.com/notes/study/image-processing/robot-vision/chapter-3/binary-image-moment/binary-image-moment
• https://www.zywvvd.com/notes/study/image-processing/robot-vision/chapter-3/binary-image-moment/binary-image-moment