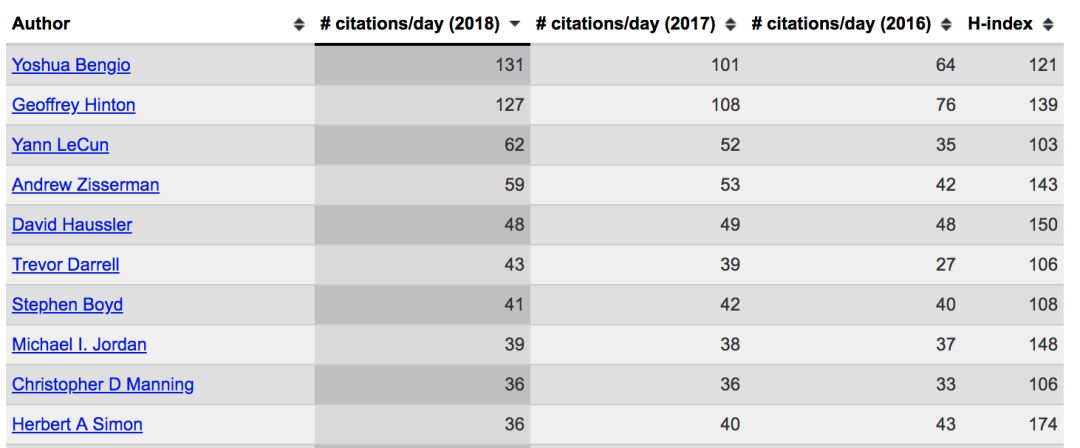
下图是2018年计算机科学领域的H-index排名前十，相信从中就是小白们也能看到不少熟悉的名字。

下图是2018年计算机科学领域的H-index排名前十，相信从中就是小白们也能看到不少熟悉的名字。

同态加密（Homomorphic encryption）是一种加密形式，它允许人们对密文进行特定形式的代数运算得到仍然是加密的结果，将其解密所得到的结果与对明文进行同样的运算结果一样。换言之，这项技术令人们可以对加密的数据进行处理，得出正确的结果，而在整个处理过程中无需对数据进行解密。同态加密的实现效果如图所示。

同态加密（Homomorphic encryption）是一种加密形式，它允许人们对密文进行特定形式的代数运算得到仍然是加密的结果，将其解密所得到的结果与对明文进行同样的运算结果一样。换言之，这项技术令人们可以对加密的数据进行处理，得出正确的结果，而在整个处理过程中无需对数据进行解密。同态加密的实现效果如图所示。

Recent advances in human stem cell-derived brain organoids promise to replicate critical molecular and cellular aspects of learning and memory and possibly aspects of cognition in vitro. Coining the term “organoid intelligence” (OI) to encompass these developments, we present a collaborative program to implement the vision of a multidisciplinary field of OI. This aims to establish OI as a form of genuine biological computing that harnesses brain organoids using scientific and bioengineering advances in an ethically responsible manner. Standardized, 3D, myelinated brain organoids can now be produced with high cell density and enriched levels of glial cells and gene expression critical for learning. Integrated microfluidic perfusion systems can support scalable and durable culturing, and spatiotemporal chemical signaling. Novel 3D microelectrode arrays permit high-resolution spatiotemporal electrophysiological signaling and recording to explore the capacity of brain organoids to recapitulate the molecular mechanisms of learning and memory formation and, ultimately, their computational potential. Technologies that could enable novel biocomputing models via stimulus-response training and organoid-computer interfaces are in development. We envisage complex, networked interfaces whereby brain organoids are connected with real-world sensors and output devices, and ultimately with each other and with sensory organ organoids (e.g. retinal organoids), and are trained using biofeedback, big-data warehousing, and machine learning methods. In parallel, we emphasize an embedded ethics approach to analyze the ethical aspects raised by OI research in an iterative, collaborative manner involving all relevant stakeholders. The many possible applications of this research urge the strategic development of OI as a scientific discipline. We anticipate OI-based biocomputing systems to allow faster decision-making, continuous learning during tasks, and greater energy and data efficiency. Furthermore, the development of “intelligence-in-

kafka 传统上被视为一个强大的消息总线，能够处理事件流，但是不具备对数据的处理和转换能力。kafka可靠的流处理能力，使其成为流处理系统的完美数据源，Apache Storm，Apache Spark streams,Apache Flink,Apache samza 的流处理系统都是基于kafka构建的，而kafka通常是它们唯一可靠的数据源。 行业分析师有时候声称，所有这些流处理系统就像已存在了近20年的复杂事件处理系统一样。我们认为流处理变得更加流行是因为它是在kafka之后创建的，因此可以使用kafka做为一个可靠的事件流处理源。日益流行的apache kafka,首先做为一个简单的消息总线，后来做为一个数据集成系统，许多公司都有一个系统包含许多有趣的流数据，存储了大量的具有时间和具有时许性的等待流处理框架处理的数据。换句话说，在数据库发明之前，数据处理明显更加困难，流处理由于缺乏流处理平台而受到阻碍。 从版本0.10.0开始，kafka不仅仅为每个流行的流处理框架提供了更可靠的数据来源。现在kafka包含了一个强大的流处理数据库作为其客户端集合的一部分。这允许开发者在自己的应用程序中消费，处理和生成事件，而不以来于外部处理框架。 在本章开始，我们将解释流处理的含义，因为这个术语经常被误解，然后讨论流处理的一些基本概念和所有流处理系统所共有的设计模式。然后我们将深入讨论Apache kafka的流处理库，它的目标和架构。我们将给出一个如何使用kafka流计算股票价格移动平均值的小例子。然后我们将讨论其他好的流处理的例子，并通过提供一些标准来结束本章。当你选择在apache中使用哪个流处理框架时可以根据这些标准进行权衡。本章简要介绍流处理，不会涉及kafka中流的每一个特性。也不会尝试讨论和比较现有的每一个流处理框架，这些主题值得写成整本书，或者几本书。

kafka 传统上被视为一个强大的消息总线，能够处理事件流，但是不具备对数据的处理和转换能力。kafka可靠的流处理能力，使其成为流处理系统的完美数据源，Apache Storm，Apache Spark streams,Apache Flink,Apache samza 的流处理系统都是基于kafka构建的，而kafka通常是它们唯一可靠的数据源。 行业分析师有时候声称，所有这些流处理系统就像已存在了近20年的复杂事件处理系统一样。我们认为流处理变得更加流行是因为它是在kafka之后创建的，因此可以使用kafka做为一个可靠的事件流处理源。日益流行的apache kafka,首先做为一个简单的消息总线，后来做为一个数据集成系统，许多公司都有一个系统包含许多有趣的流数据，存储了大量的具有时间和具有时许性的等待流处理框架处理的数据。换句话说，在数据库发明之前，数据处理明显更加困难，流处理由于缺乏流处理平台而受到阻碍。 从版本0.10.0开始，kafka不仅仅为每个流行的流处理框架提供了更可靠的数据来源。现在kafka包含了一个强大的流处理数据库作为其客户端集合的一部分。这允许开发者在自己的应用程序中消费，处理和生成事件，而不以来于外部处理框架。 在本章开始，我们将解释流处理的含义，因为这个术语经常被误解，然后讨论流处理的一些基本概念和所有流处理系统所共有的设计模式。然后我们将深入讨论Apache kafka的流处理库，它的目标和架构。我们将给出一个如何使用kafka流计算股票价格移动平均值的小例子。然后我们将讨论其他好的流处理的例子，并通过提供一些标准来结束本章。当你选择在apache中使用哪个流处理框架时可以根据这些标准进行权衡。本章简要介绍流处理，不会涉及kafka中流的每一个特性。也不会尝试讨论和比较现有的每一个流处理框架，这些主题值得写成整本书，或者几本书。

输入（Input）/输出（Output）设备，即I/O设备。 显示器这所谓的输出设备。 鼠标和键盘所谓的输入设备。 硬盘，数据持久化。

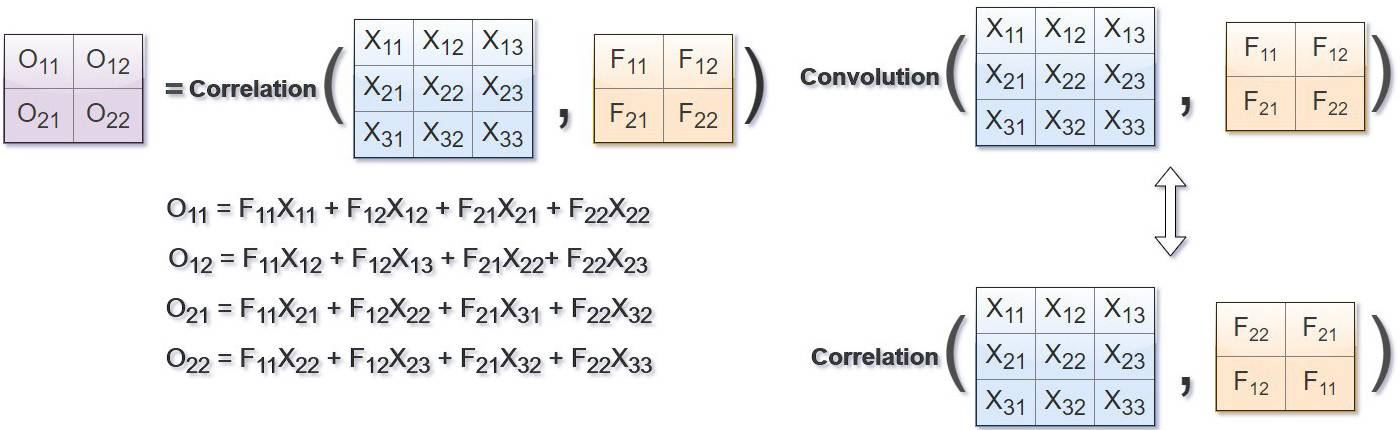
在计算机视觉领域，卷积核、滤波器通常为较小尺寸的矩阵，比如\(3\times3\)、\(5\times5\)等，数字图像是相对较大尺寸的2维（多维）矩阵（张量），图像卷积运算与相关运算的关系如下图所示（图片来自链接），其中\(F\)为滤波器，\(X\)为图像，\(O\)为结果。

媒介和技术的发展使设计艺术打破了原本界限：从静到动到可交互，从二维到三维到沉浸体验，技术结合设计形成的审美价值在未来是无止境的。视觉设计师们普遍形成了不断从文化、艺术中汲取风格和元素，采用计算机设计软件结合自定义传达内容在媒介载体上传播的工作模式。然而设计软件赋予了设计绚丽的视觉语言却也限制了内在的可能性：设计在不断反复之前出现的文化浪潮，许多设计因软件功能出现了泛同质化难以应对复杂多变的应用场景。现有的设计语言不够丰富，而生成艺术的发展优化了设计创造力的新路径。正如维拉·莫尔纳所言：“这听起来可能很矛盾

媒介和技术的发展使设计艺术打破了原本界限：从静到动到可交互，从二维到三维到沉浸体验，技术结合设计形成的审美价值在未来是无止境的。视觉设计师们普遍形成了不断从文化、艺术中汲取风格和元素，采用计算机设计软件结合自定义传达内容在媒介载体上传播的工作模式。然而设计软件赋予了设计绚丽的视觉语言却也限制了内在的可能性：设计在不断反复之前出现的文化浪潮，许多设计因软件功能出现了泛同质化难以应对复杂多变的应用场景。现有的设计语言不够丰富，而生成艺术的发展优化了设计创造力的新路径。正如维拉·莫尔纳所言：“这听起来可能很矛盾

媒介和技术的发展使设计艺术打破了原本界限：从静到动到可交互，从二维到三维到沉浸体验，技术结合设计形成的审美价值在未来是无止境的。视觉设计师们普遍形成了不断从文化、艺术中汲取风格和元素，采用计算机设计软件结合自定义传达内容在媒介载体上传播的工作模式。然而设计软件赋予了设计绚丽的视觉语言却也限制了内在的可能性：设计在不断反复之前出现的文化浪潮，许多设计因软件功能出现了泛同质化难以应对复杂多变的应用场景。现有的设计语言不够丰富，而生成艺术的发展优化了设计创造力的新路径。正如维拉·莫尔纳所言：“这听起来可能很矛盾

输入（Input）/输出（Output）设备，即I/O设备。 显示器这所谓的输出设备。 鼠标和键盘所谓的输入设备。 硬盘，数据持久化。

你好，我是对白，清华计算机硕士，BAT算法工程师，拿过8家大厂算法岗SSP offer。

你好，我是对白，清华计算机硕士，BAT算法工程师，拿过8家大厂算法岗SSP offer。

Python是生物信息学应用中的常用编程语言，在2019年11月TIOBE 编程语言排行榜中排名第3，仅次于Java语言、C语言。

各位同仁们好，我们最近在2023年IEEE进化计算国际会议（IEEE CEC） 上组织了关于“进化计算机视觉和图像处理” 的Special Session，将接收所有关于进/演化计算算法应用于解决计算机视觉和图像处理问题的论文。

CPU (Central Processing Unit) 中央处理器 。 简单来说， CPU是一个超级精细的印刷电路版。

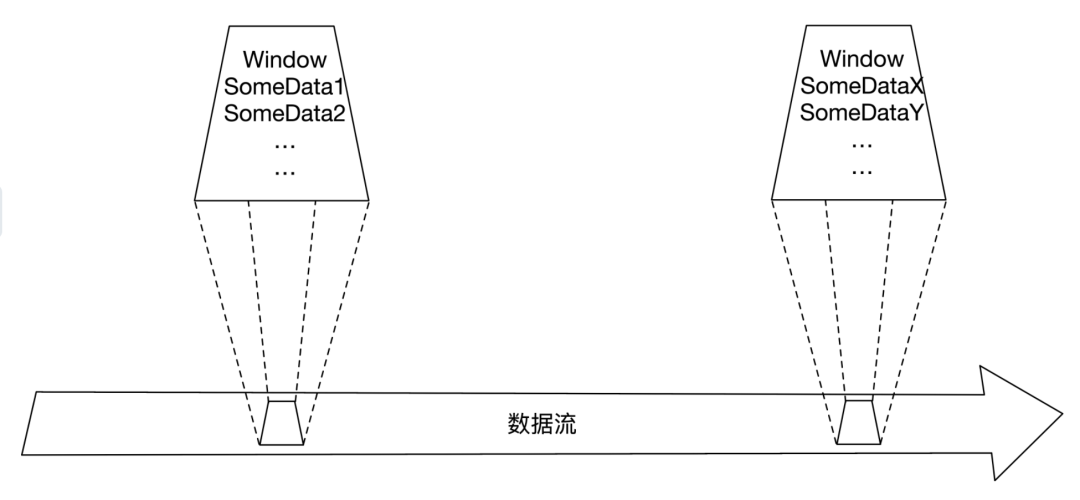
在上一章代码中使用了timeWindow，使得我们可以操作Flink流中的一个时间段内的数据，这就引出了Flink中的"窗口"概念：在大多数场景下，数据流都是"无限的"，因引我们无法等待数据流终止后才进行一些统计计算，而通常的需求是对一段时间或是一定范围内的数据进行分析。

图像处理中会遇到需要计算物体朝向的情况，前文使用转动惯量计算了物体朝向，本文换一种思路，使用投影统计计算朝向。 问题描述 📷 对于一幅二值图像，需要求解图像的朝向 解决思路 物体上的每个点可以向某个方向投影，完成投影后每个点变为一维数据 📷 直觉上，与真正朝向垂直方向的投影的一维数据，的方差是最小的 按照这个思路，求解二值图物体朝向 计算方法 图中非零的点有 N 个，坐标为 (x_i, y_i), 0 <i<N \textbf{x}=[x_1,x_2, …,x_N]^T, \textbf{y}=[y_