文章目录- I . 人类的视觉原理
- II . 卷积神经网络 模仿 视觉原理
- III . 卷积神经网络简介
- IV . 卷积神经网络 组成
- V . 卷积神经网络 工作流程
- VI . 降低样本参数数量级
- VII . 卷积计算 图示分析
- VIII . 卷积计算 简介
- IX . 卷积计算 示例
- X . 卷积本质
- XI . 卷积 计算 参数
I . 人类的视觉原理
1 . 深度学习 与 大脑认知 :
① 深度学习基础 : 大脑对外界事务的认知原理 , 是很多深度学习算法的基础 , 这里讨论人类的视觉原理 ,
② 视觉原理 : 视觉识别信息处理过程 , 是由可视皮层完成的 , 并且可视皮层是分级的 ;
③ 卷积神经网络来源 : 卷积神经网络 受 人类视觉原理启发 , 而开发出来的 ;
2 . 视觉原理 与 可视皮层 分层 :
① 信号输入 : 视觉输入原始信号 , 即大脑从瞳孔中摄入一张由像素值组成的图片 ;
② 识别边缘 ( 可视皮层 底层 ) : 将输入的像素值 , 进行 初步处理 , 识别像素的 边缘 , 方向 信息 ;
③ 识别形状 ( 可视皮层 中层 ) : 将 边缘信息 抽象成 形状信息 , 如圆形 , 方形等 ;
④ 判定类别 ( 可视皮层 上层 ) : 在上述识别形状的基础上 , 判定该形状是什么类型的事务 , 如桌子 , 汽车等 ;
II . 卷积神经网络 模仿 视觉原理
卷积神经网络 原理 :
① 模拟视觉原理 : 人类视觉识别涉及到了 不同层级 的可视皮层 , 每层分别处理不同的事务 ;
② 构建多层神经网络模型 : 模仿上述分层的课视频曾 , 创建多层神经网络模型 , 如 卷积神经网络 ;
③ 分层工作机制 : 多层神经网络模型机制 , 在底层识别图像的边缘特征 , 上一层逐渐识别形状 , 最上层对图像像素进行判定分类 ;
III . 卷积神经网络简介
卷积神经网络 简介 :
① CNN 卷积神经网络 处理的数据类型 : CNN 卷积神经网络 , 是特殊的神经网络 , 其通常用于处理网格状的数据 , 如 时间序列 ( 音频数据 ) , 或 图片数据 ;
② CNN 适用场景 : CNN 卷积神经网络其本质是一个多层神经网络 , 该模型适合处理 大型图像 相关的 机器学习 问题 ;
③ CNN 成就 : CNN 在 深度神经网络 中是应用最早 , 最成功的的领域 ;
④ CNN 的计算 : 卷积神经网络其本质还是 神经网络 , 其基本的计算由 矩阵相乘 变成了 卷积 ;
⑤ CNN 处理图像原理 : 处理大型图像时 , 将图像识别问题 降维处理 , 从底层向高层 , 不断抽取特征时 , 其维度越降越低 , 最终将其变成可训练的模型 ;
IV . 卷积神经网络 组成
卷积神经网络 构成 :
① 组成 : 卷积神经网络由 卷积层 , 池化层 , 全连接层 , 组成 ;
② 卷积组 : 卷积层 与 池化层 , 配对组合 , 即
个卷积 +
个池化 , 组成
个卷积组 ; 整个卷积神经网络中有多个卷积组 ;
③ 工作机制 : 按照上述分层 , 逐层提取数据 ( 图像 ) 特征 , 这些特征通过全连接层结合起来 , 完成最终的分类判定操作 ;
V . 卷积神经网络 工作流程
卷积神经网络 工作流程 :
① 卷积 : 通过卷积 模拟 特征 ;
② 池化 : 通过卷积的 权值 共享 , 池化 , 可以降低整体网络的参数数量级 ;
③ 连接分类 : 上述 卷积 池化 后的结果通过传统的 神经网络 进行分类即可 ;
VI . 降低样本参数数量级
1 . 传统神经网络分析图片 : 使用 传统神经网络 分析一张图片 , 如果该图片有
万 像素 , 那么需要将每个像素值都作为一个属性值输入到神经网络中 , 那么其隐藏层有
万神经元单元 , 如果这样的图片有几万张 , 这个数量级太复杂 ;
2 . 卷积神经网络 减少参数数量级 原理 :
① 底层特征局部性 : 图像的最底层的特征都是局部性的 , 使用一个小的过滤器 , 如
像素 , 就可以将图像的 边缘 特征表示出来 ; 边缘底层特征是 横向 , 垂直 , 斜线 , 等边缘 形状特征 ;
② 图像特征类似 : 图像中的特征 , 不管是相同图像 , 还是不同图像 , 其中的片段的特征是类似的 , 可以使用 同一组分类器 描述 不同的图像 特征 ; 如训练识别一只猫的图像 , 在这张图片上的猫 , 与另外一张图片的猫 , 其片段特征的是类似的 ;
③ 降低数量级 :
万像素的图片 , 可以使用
万个
像素 的过滤器 , 描述图片底部的特征 ;
VII . 卷积计算 图示分析
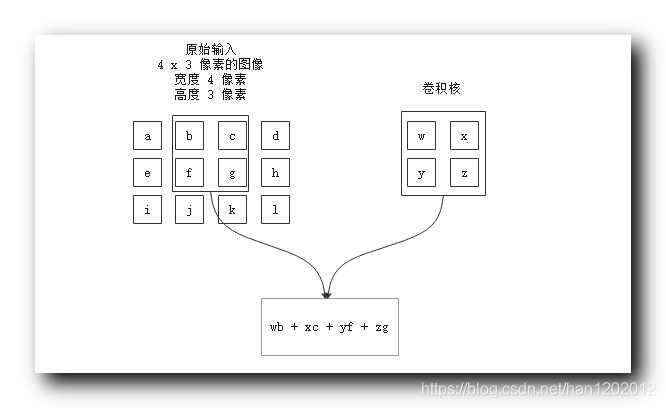
1 . 原始输入 与 卷积核 :
① 原始输入 : 需要识别的图像 ;
② 卷积核 : 可以看做是滑动窗口 , 在图像上滑动 ;

2 . 第
次卷积 :
与 卷积核
进行卷积 计算 : 如下图 , 对应位置的值相乘 , 然后将
个乘积相加 , 这个操作表示一次卷积运算 , 结果是
;

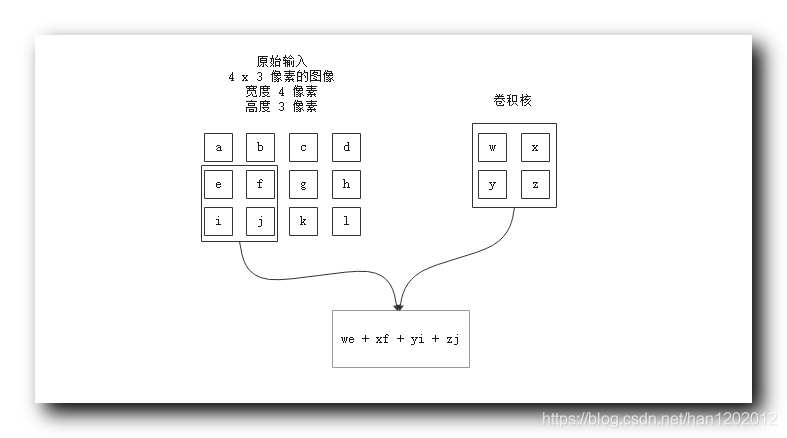
3 . 第
次卷积 :
与 卷积核
进行卷积 计算 : 如下图 , 对应位置的值相乘 , 然后将
个乘积相加 , 这个操作表示一次卷积运算 , 结果是
;
4 . 第
次卷积 :
与 卷积核
进行卷积 计算 : 如下图 , 对应位置的值相乘 , 然后将
个乘积相加 , 这个操作表示一次卷积运算 , 结果是
;

5 . 第
次卷积 :
与 卷积核
进行卷积 计算 : 如下图 , 对应位置的值相乘 , 然后将
个乘积相加 , 这个操作表示一次卷积运算 , 结果是
;
6 . 第
次卷积 :
与 卷积核
进行卷积 计算 : 如下图 , 对应位置的值相乘 , 然后将
个乘积相加 , 这个操作表示一次卷积运算 , 结果是
;

7 . 第
次卷积 :
与 卷积核
进行卷积 计算 : 如下图 , 对应位置的值相乘 , 然后将
个乘积相加 , 这个操作表示一次卷积运算 , 结果是
;

8 . 卷积结如下 : 变成了一个
的图像 ;

9 . 卷积效果 :
① 卷积 结果 : 原来的输入图像是
像素 , 经过卷积后 , 变成了
的图像 ;
② 效果 : 维度降低了 , 参数变少了 ;
③ 卷积核维度 : 如果使用
的卷积核 , 那么维度降低的更多 ;
VIII . 卷积计算 简介
1 . 卷积计算 :
① 输入图 : 要分析的图片 , 又叫做特征图 ;
② 卷积核 :大小是固定的 , 用于扫描输入图 ; 可以由学习得到 , 也可以使用事先设计好的卷积核 ;
③ 内积运算 : 就是所有对应元素相乘 , 然后求和的结果 ;
③ 卷积计算过程 : 使用卷积核 扫描 输入图 , 如上示例 , 将扫描到的 输入图的部分内容 , 与卷积核的内容 , 进行内积运算 ;
2 . 常用的卷积核 :
① 常用卷积核 1 :
0 | 0 | 0 |
|---|---|---|
0 | 0 | 0 |
0 | 0 | 0 |
② 常用卷积核 2 :
-1 | -1 | -1 |
|---|---|---|
0 | 0 | 0 |
1 | 1 | 1 |
③ 常用卷积核 3 :
-1 | 0 | 1 |
|---|---|---|
-1 | 0 | 1 |
-1 | 0 | 1 |
IX . 卷积计算 示例
计算图中的最后两个空白位置的卷积 :
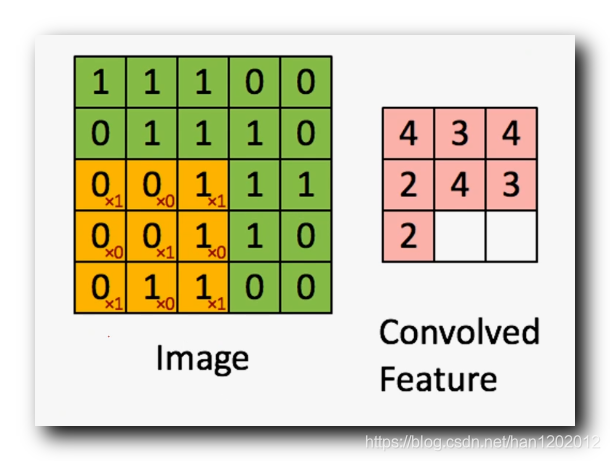
输入图是
的 , 卷积核是
的 ;
黄色部分是卷积核为 :
卷积计算过程如下 :
① 第
行第
列 卷积结果 : 卷积核
与
进行卷积运算 , 如下 :
② 第
行第
列 卷积结果 : 卷积核
与
进行卷积运算 , 如下 :
X . 卷积本质
1 . 卷积 及 卷积核 本质 :
① 卷积核本质 : 卷积核的本质相当于一个过滤器 , 可以过滤识别图像的各个区域的特征 , 获取这些区域的特征值 ;
② 卷积核来源 : 卷积核一般是在学习训练过程中得到的 ;
③ 卷积结果的意义 : 每个卷积核代表了一种图像的特征模式 , 如果某个区域与该卷积核 进行内积运算 , 卷积出的值很大 , 说明该区域与该卷积核图像类似 ;
④ 多个卷积核 : 在实际使用中 , 一个卷积神经网络 , 可能会有多个卷积核 ;
2 . 卷积核底层纹理 :
① 底层纹理模式 : 如果有
个卷积核 , 可以理解为该图像有
种底层的纹理模式 , 使用这些纹理模式的特征可以绘制出一幅图像 , 也能从一堆杂乱的图像中识别出该图像 ;
② 底层纹理示例 : 下图是常用的
种卷积核 , 也就是
种底层纹理模式 ; 如 第
行 , 第
列 , 三条垂直的线 , 亮线表示 1 , 暗线表示 0 , 因此可以使用卷积核
表示 , 该纹理 , 最左侧是亮的 , 右边两个是暗的 ;

XI . 卷积 计算 参数
1 . 通道数 : 卷积核的个数 ;
① 输入通道数 : 上一层输出的通道数量 , 即卷积核的个数 ;
② 输出通道数 : 本层输出的通道数量 , 即卷积核的个数 ;
2 . 卷积核大小 :
① 卷积核大小关联性 : 与卷积计算后 , 每个卷积结果输出值 , 与多大范围的输入图像有关 , 即上面说的过滤器大小 , 底层纹理大小 , 滑动窗口大小 ;
② 建议取值 : 建议使用奇数大小 , 这样能保证卷积计算后 , 有唯一的一个中心点 ;
③ 卷积核效果 : 卷积核 越大 , 分类效果越好 ;
④ 卷积核参数数量 : 卷积核增大 , 其参数就会指数级增加 , 参数个数是卷积核的平方 , 即进行内积运算的参数个数 ; 如卷积核为
, 那么参数有
个 , 卷积核为
, 参数有
个 ;
3 . 填充 : 不想降维 , 先将输入图 对称 补
, 然后进行滑动窗口 , 卷积计算 ;
① 降低维度 : 卷积之后 , 不想降维 , 如前面的
的输入图 , 使用
卷积核 , 卷积之后变成了
的图像 , 这里就将输入图的维度下降了 ;
② 对称补
: 如果不想降低输入图的维度 , 可以使用填充 , 即先在周边位置使用
补充 , 注意对称补充 , 不要在一个边上补
, 然后再进行卷积计算 ;
4 . 步长 : 每次卷积核的移动距离 ( 单位 : 像素 ) , 即 每次移动滑动窗口 ( 卷积核 ) 的距离 , 单位是像素 , 之前的两个例子都是每次移动一个像素值 ;