不对称因子g的理论计算

发布于

不对称因子g是分子不对称程度的一种度量，在研究手性化合物的光物理性质时是一个很重要的参数。手性化合物与光发生作用，会产生圆二色谱（CD）和圆偏振发光（CPL）两种光谱，前者为吸收，后者为发射，它们的关系类似紫外-可见吸收和荧光发射间的关系。大致原理可参考下图[1]：

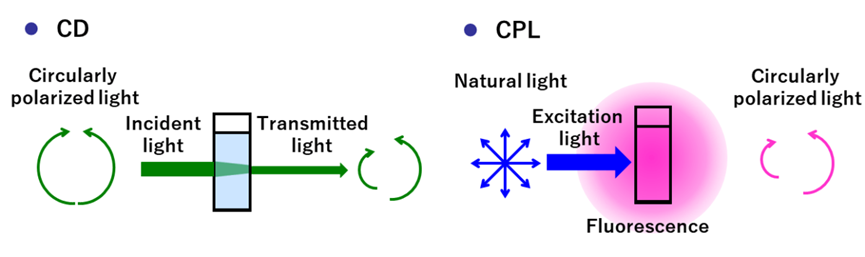
本文简单介绍一下不对称因子的理论计算方法，并附一个笔者自己用的处理数据的Python脚本。本文只介绍吸收不对称因子（gabs）的计算，而圆偏振发光不对称因子（glum）的计算与之类似，只不过两者使用的结构不同：前者使用基态的结构，而后者使用S1的结构。从计算的角度来说，经过理论推导，g因子的计算表达式为[2]

其中，μ为跃迁电偶极矩，m为跃迁磁偶极矩，θ为两者之间的夹角。一般来说，|m|在10−20数量级，而|μ|在10−18数量级，后者远大于前者，所以上式可简化为

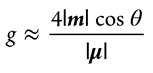
一般文献中也都是用此式来计算和讨论g因子的。

下面以王小野老师J. Am. Chem. Soc. 2021, 143, 17958一文中的1a体系为例，说明g因子的计算方法，结构取自文章的支撑材料，使用软件为Gaussian 16 C.01。其输入文件为

代码语言：javascript
复制
%mem=200GB
%nprocs=48
%chk=1a.chk
#p pbe1pbe/6-311G* td(nstates=20)

1a


0 1

C 1.203952 -0.683746 0.175929

C 1.204013 0.683659 -0.176090

C 0.000028 1.410659 -0.000136

C -1.203985 0.683770 0.175854

C -1.204047 -0.683673 -0.176026

C -0.000089 -1.410654 -0.000030

N 2.320665 -1.369076 0.647141

N -2.320876 -1.368938 -0.647108

N -2.320739 1.369104 0.647008

N 2.320801 1.368918 -0.647235

C 2.409623 -2.749083 0.580317

C 3.670872 -3.165436 1.053379

C 4.341225 -1.976828 1.533780

C 3.464537 -0.889880 1.310210

C 3.464658 0.889672 -1.310297

C 4.341451 1.976562 -1.533748

C 3.671180 3.165193 -1.053290

C 2.409871 2.748914 -0.580323

C -3.464703 -0.889736 -1.310243

C -4.341481 -1.976653 -1.533647

C -3.671198 -3.165250 -1.053154

C -2.409893 -2.748939 -0.580206

C -2.409641 2.749116 0.580213

C -3.670885 3.165497 1.053268

C -4.341252 1.976916 1.533685

C -3.464583 0.889942 1.310140

C -3.976658 -4.519126 -1.013645

C -3.015144 -5.414378 -0.533690

C -1.750049 -4.976223 -0.149296

C -1.383383 -3.616184 -0.184407

C -3.753778 0.381405 -1.798074

C -4.967102 0.561628 -2.454576

C -5.868033 -0.492709 -2.635121

C -5.554113 -1.769611 -2.187234

C -5.553871 1.769917 2.187310

C -5.867882 0.492997 2.635085

C -4.967057 -0.561405 2.454388

C -3.753747 -0.381224 1.797848

C -1.383076 3.616302 0.184429

C -1.749620 4.976378 0.149464

C -3.014653 5.414613 0.533972

C -3.976224 4.519405 1.013897

C 1.383092 -3.616270 0.184484

C 1.749654 -4.976346 0.149472

C 3.014704 -5.414552 0.533958

C 3.976244 -4.519334 1.013941

C 5.553896 -1.769748 2.187279

C 5.867930 -0.492775 2.634896

C 4.967097 0.561608 2.454154

C 3.753734 0.381347 1.797725

C 3.753769 -0.381539 -1.797905

C 4.967145 -0.561853 -2.454295

C 5.868080 0.492465 -2.634911

C 5.554134 1.769429 -2.187207

C 3.976669 4.519061 -1.013738

C 3.015184 5.414328 -0.533736

C 1.750076 4.976206 -0.149351

C 1.383396 3.616164 -0.184484

B -0.000126 -2.960010 0.000037

B 0.000108 2.960016 -0.000196

H -4.943514 -4.881991 -1.353008

H -3.251475 -6.473753 -0.486644

H -1.027199 -5.711814 0.189515

H -3.059600 1.206672 -1.696989

H -5.211425 1.547534 -2.839801

H -6.808461 -0.315041 -3.148662

H -6.233086 -2.600370 -2.360239

H -6.232763 2.600718 2.360428

H -6.808303 0.315361 3.148650

H -5.211453 -1.547329 2.839522

H -3.059647 -1.206544 1.696634

H -1.026726 5.711933 -0.189330

H -3.250891 6.474013 0.487032

H -4.943028 4.882327 1.353345

H 1.026788 -5.711905 -0.189367

H 3.250973 -6.473944 0.486998

H 4.943060 -4.882253 1.353361

H 6.232816 -2.600517 2.360441

H 6.808380 -0.315091 3.148393

H 5.211536 1.547577 2.839143

H 3.059637 1.206656 1.696428

H 3.059597 -1.206796 -1.696714

H 5.211514 -1.547813 -2.839354

H 6.808536 0.314740 -3.148380

H 6.233133 2.600153 -2.360274

H 4.943534 4.881919 -1.353082

H 3.251544 6.473696 -0.486688

H 1.027253 5.711804 0.189497

可以看出，这就是一个常规的TD计算。计算完成后，在输出文件中，我们可以依次找到：

代码语言：javascript
复制
Ground to excited state transition electric dipole moments (Au):

state          X           Y           Z        Dip. S.      Osc.

1        -2.1747     -0.0000     -0.0000      4.7293      0.2519

2        -0.0000     -0.0001     -0.6596      0.4351      0.0288

3         0.0000     -0.3133     -0.0001      0.0982      0.0077

4         0.0000      0.0006     -0.5477      0.3000      0.0241

和

代码语言：javascript
复制
Ground to excited state transition magnetic dipole moments (Au):

state          X           Y           Z

1        -0.2492      0.0000     -0.0000

2        -0.0000      0.0000      1.4332

3        -0.0000      0.1486      0.0003

4        -0.0000      0.0001      2.1894

这两段就是从基态到所计算的所有激发态（为节省篇幅，此处只展示了前4个激发态）的跃迁电偶极矩和跃迁磁偶极矩，它们都是矢量，有X、Y、Z三个分量，拿这三个分量，利用高中空间向量的知识，就可以求出g因子了。

实际计算中，需要注意单位换算的问题，Gaussian计算给出的是原子单位，而计算g因子时需要使用CGS制，它们的换算关系如下：

1 a.u. = 2.5412 Debye = 2.5412×10−18 esu cm

1 a.u. = 1.8548×10−23J/T = 1.8548×10−20 erg G−1

为了一劳永逸，笔者写了一个简单的脚本，可以直接输出|μ|、|m|和cosθ的值，其内容如下：

代码语言：javascript
复制
#!/usr/bin/env python


import sys,math

name = sys.argv[1]

nprint = 1


logfile = open(name)

elefound = False

magfound = False

nstate = 0

elevec = []

magvec = []

for line in logfile:

if line[0:51] == " Ground to excited state transition electric dipole":

elefound = True

continue

if elefound:

if line[0:12] == "       state":

continue

if line[0:51] == " Ground to excited state transition velocity dipole":

elefound = False

continue

else:

nstate = nstate + 1

tmplist = []

tmplist.append(int(line.split()[0]))

tmplist.append(float(line.split()[1]))

tmplist.append(float(line.split()[2]))

tmplist.append(float(line.split()[3]))

elevec.append(tmplist)


if line[0:51] == " Ground to excited state transition magnetic dipole":
    magfound = True
    continue
if magfound:
    if line[0:12] == "       state":
        continue
    if line[0:51] == " Ground to excited state transition velocity quadru":
        magfound = False
        break
    else:
        tmplist = []
        tmplist.append(int(line.split()[0]))
        tmplist.append(float(line.split()[1]))
        tmplist.append(float(line.split()[2]))
        tmplist.append(float(line.split()[3]))
        magvec.append(tmplist)



nprint = nstate #输出态的数目，默认输出所有的态

for i in range(0,nprint):

elelist = elevec[i]

X1 = elelist[1]

Y1 = elelist[2]

Z1 = elelist[3]

maglist = magvec[i]

X2 = maglist[1]

Y2 = maglist[2]

Z2 = maglist[3]

absmiu_au = (X1X1+Y1Y1+Z1Z1)**0.5

absmiu = absmiu_au/0.393456 # Debye or 10^-18 esu cm

absm_au = (X2X2+Y2Y2+Z2Z2)**0.5

absm = absm_au1.8548 #unit 10^-20 erg/G

dotmium = X1X2+Y1Y2+Z1Z2

costheta = dotmium/(absmiu_au*absm_au)

#完整表达式：


g = 4costhetaabsmiu*(1E-18)absm(1E-20)/((absmiu*(1E-18))*2+(absm(1E-20))**2)


#简化表达式：
g = 4*costheta*absm*(1E-20)/(absmiu*(1E-18))

print("state    %d" %(i+1))
print("absmiu   %f 10^-18 esu cm" %(absmiu) )
print("absm     %f 10^-20 erg/G" %absm )
print("costheta %f" %costheta )
print("g        %f" %g )
g = g*1000
print("g*1000   %f" %g )
print()

关于脚本的内容，此处就不做阐释了，稍微懂一点Python的读者都能看懂。设脚本名称为calcg.py，则运行方式为

代码语言：javascript
复制
./calcg.py XXX.log

即以输出文件名为输入参数即可，程序会输出：

代码语言：javascript
复制
state    1

absmiu   5.527175 10^-18 esu cm

absm     0.462216 10^-20 erg/G

costheta 1.000000

g        0.003345

g*1000   3.345045


state    2

absmiu   1.676426 10^-18 esu cm

absm     2.658299 10^-20 erg/G

costheta -1.000000

g        -0.063428

g*1000   -63.427763

与文献中的结果一致：

作为练习，读者可以计算一下1b和1c，看能否重复文献结果。

参考文献：

[1] https://jascoinc.com/learning-center/theory/spectroscopy/basics-of-circular-polarized-luminescence/

[2] Chem. Rev. 2021, 121, 2373−2412

#append#line#state#程序#脚本