城市生态与人类生活息息相关,快速 、准确 、客 观地了解城市生态状况已成为生态领域的一个研究重点 。基于遥感技术,提出一个完全基于遥感技术 ,以自然因子为主的遥感生态指数 (RSEI)来对城市的生态状况进行快速监测与评价 。该指数利用主成分分析技术集成了植被指数 、湿度分量、地表温度和建筑指数等 4个评价指标,它们分别代表了绿度、湿度、热度和干度等4大生态要素。 本文基于GEE平台,实现RSEI算法。 运行结果:
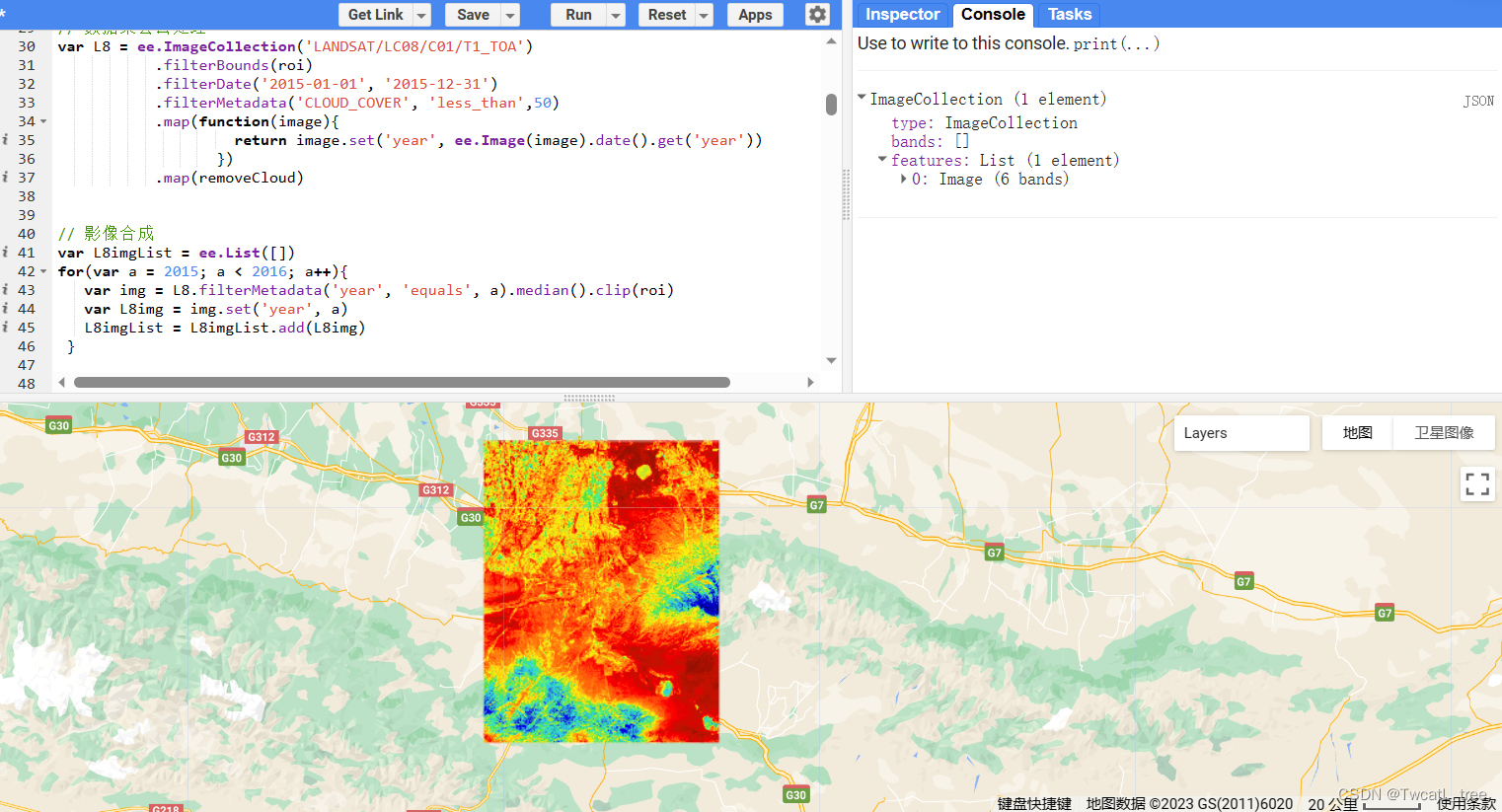
第一步:定义研究区,自行更换自己的研究区 第二步:加载数据集,定义去云函数 第三步:主函数,计算生态指标 第四步:PCA融合,提取第一主成分 第五步:利用PC1,计算RSEI,并归一化
完整代码
代码如下(示例):
// 第一步:定义研究区,自行更换自己的研究区 var roi = /* color: #98ff00 */ /* displayProperties: [ { "type": "rectangle" } ] */ ee.Geometry.Polygon( [[[120.1210075098537, 35.975189051414006], [120.1210075098537, 35.886229778229115], [120.25764996590839, 35.886229778229115], [120.25764996590839, 35.975189051414006]]], null, false);Map.centerObject(roi);
// 第二步:加载数据集,定义去云函数
function removeCloud(image){
var qa = image.select('BQA')
var cloudMask = qa.bitwiseAnd(1 << 4).eq(0)
var cloudShadowMask = qa.bitwiseAnd(1 << 8).eq(0)
var valid = cloudMask.and(cloudShadowMask)
return image.updateMask(valid)
}// 数据集去云处理
var L8 = ee.ImageCollection('LANDSAT/LC08/C01/T1_TOA')
.filterBounds(roi)
.filterDate('2018-01-01', '2019-12-31')
.filterMetadata('CLOUD_COVER', 'less_than',50)
.map(function(image){
return image.set('year', ee.Image(image).date().get('year'))
})
.map(removeCloud)// 影像合成
var L8imgList = ee.List([])
for(var a = 2018; a < 2020; a++){
var img = L8.filterMetadata('year', 'equals', a).median().clip(roi)
var L8img = img.set('year', a)
L8imgList = L8imgList.add(L8img)
}// 第三步:主函数,计算生态指标
var L8imgCol = ee.ImageCollection(L8imgList)
.map(function(img){
return img.clip(roi)
})L8imgCol = L8imgCol.map(function(img){
// 湿度函数:Wet
var Wet = img.expression('B*(0.1509) + G*(0.1973) + R*(0.3279) + NIR*(0.3406) + SWIR1*(-0.7112) + SWIR2*(-0.4572)',{
'B': img.select(['B2']),
'G': img.select(['B3']),
'R': img.select(['B4']),
'NIR': img.select(['B5']),
'SWIR1': img.select(['B6']),
'SWIR2': img.select(['B7'])
})
img = img.addBands(Wet.rename('WET'))// 绿度函数:NDVI
var ndvi = img.normalizedDifference(['B5', 'B4']);
img = img.addBands(ndvi.rename('NDVI'))// 热度函数:lst 直接采用MODIS产品
var lst = ee.ImageCollection('MODIS/006/MOD11A1').map(function(img){
return img.clip(roi)
})
.filterDate('2014-01-01', '2019-12-31')var year = img.get('year')
lst=lst.filterDate(ee.String(year).cat('-01-01'),ee.String(year).cat('-12-31')).select(['LST_Day_1km', 'LST_Night_1km']);// reproject主要是为了确保分辨率为1000
var img_mean=lst.mean().reproject('EPSG:4326',null,1000);
//print(img_mean.projection().nominalScale())img_mean = img_mean.expression('((Day + Night) / 2)',{
'Day': img_mean.select(['LST_Day_1km']),
'Night': img_mean.select(['LST_Night_1km']),
})
img = img.addBands(img_mean.rename('LST'))// 干度函数:ndbsi = ( ibi + si ) / 2
var ibi = img.expression('(2 * SWIR1 / (SWIR1 + NIR) - (NIR / (NIR + RED) + GREEN / (GREEN + SWIR1))) / (2 * SWIR1 / (SWIR1 + NIR) + (NIR / (NIR + RED) + GREEN / (GREEN + SWIR1)))', {
'SWIR1': img.select('B6'),
'NIR': img.select('B5'),
'RED': img.select('B4'),
'GREEN': img.select('B3')
})
var si = img.expression('((SWIR1 + RED) - (NIR + BLUE)) / ((SWIR1 + RED) + (NIR + BLUE))', {
'SWIR1': img.select('B6'),
'NIR': img.select('B5'),
'RED': img.select('B4'),
'BLUE': img.select('B2')
})
var ndbsi = (ibi.add(si)).divide(2)
return img.addBands(ndbsi.rename('NDBSI'))
})var bandNames = ['NDVI', "NDBSI", "WET", "LST"]
L8imgCol = L8imgCol.select(bandNames)//定义归一化函数:归一化
var img_normalize = function(img){
var minMax = img.reduceRegion({
reducer:ee.Reducer.minMax(),
geometry: roi,
scale: 1000,
maxPixels: 10e13,
})
var year = img.get('year')
var normalize = ee.ImageCollection.fromImages(
img.bandNames().map(function(name){
name = ee.String(name);
var band = img.select(name);
return band.unitScale(ee.Number(minMax.get(name.cat('_min'))), ee.Number(minMax.get(name.cat('_max'))));}) ).toBands().rename(img.bandNames()).set('year', year); return normalize;}
var imgNorcol = L8imgCol.map(img_normalize);// 第四步:PCA融合,提取第一主成分
var pca = function(img){var bandNames = img.bandNames(); var region = roi; var year = img.get('year') // Mean center the data to enable a faster covariance reducer // and an SD stretch of the principal components. var meanDict = img.reduceRegion({ reducer: ee.Reducer.mean(), geometry: region, scale: 1000, maxPixels: 10e13 }); var means = ee.Image.constant(meanDict.values(bandNames)); var centered = img.subtract(means).set('year', year); // This helper function returns a list of new band names. var getNewBandNames = function(prefix, bandNames){ var seq = ee.List.sequence(1, 4); //var seq = ee.List.sequence(1, bandNames.length()); return seq.map(function(n){ return ee.String(prefix).cat(ee.Number(n).int()); }); }; // This function accepts mean centered imagery, a scale and // a region in which to perform the analysis. It returns the // Principal Components (PC) in the region as a new image. var getPrincipalComponents = function(centered, scale, region){ var year = centered.get('year') var arrays = centered.toArray(); // Compute the covariance of the bands within the region. var covar = arrays.reduceRegion({ reducer: ee.Reducer.centeredCovariance(), geometry: region, scale: scale, bestEffort:true, maxPixels: 10e13 }); // Get the 'array' covariance result and cast to an array. // This represents the band-to-band covariance within the region. var covarArray = ee.Array(covar.get('array')); // Perform an eigen analysis and slice apart the values and vectors. var eigens = covarArray.eigen(); // This is a P-length vector of Eigenvalues. var eigenValues = eigens.slice(1, 0, 1); // This is a PxP matrix with eigenvectors in rows. var eigenVectors = eigens.slice(1, 1); // Convert the array image to 2D arrays for matrix computations. var arrayImage = arrays.toArray(1) // Left multiply the image array by the matrix of eigenvectors. var principalComponents = ee.Image(eigenVectors).matrixMultiply(arrayImage); // Turn the square roots of the Eigenvalues into a P-band image. var sdImage = ee.Image(eigenValues.sqrt()) .arrayProject([0]).arrayFlatten([getNewBandNames('SD',bandNames)]); // Turn the PCs into a P-band image, normalized by SD. return principalComponents // Throw out an an unneeded dimension, [[]] -> []. .arrayProject([0]) // Make the one band array image a multi-band image, [] -> image. .arrayFlatten([getNewBandNames('PC', bandNames)]) // Normalize the PCs by their SDs. .divide(sdImage) .set('year', year); } // Get the PCs at the specified scale and in the specified region img = getPrincipalComponents(centered, 1000, region); return img;};
var PCA_imgcol = imgNorcol.map(pca)
Map.addLayer(PCA_imgcol.first(), {"bands":["PC1"]}, 'pc1')
// 第五步:利用PC1,计算RSEI,并归一化
var RSEI_imgcol = PCA_imgcol.map(function(img){
img = img.addBands(ee.Image(1).rename('constant'))
var rsei = img.expression('constant - pc1' , {
constant: img.select('constant'),
pc1: img.select('PC1')
})
rsei = img_normalize(rsei)
return img.addBands(rsei.rename('rsei'))
})
print(RSEI_imgcol)var visParam = {
palette: '040274, 040281, 0502a3, 0502b8, 0502ce, 0502e6, 0602ff, 235cb1, 307ef3, 269db1, 30c8e2, 32d3ef, 3be285, 3ff38f, 86e26f, 3ae237, b5e22e, d6e21f, fff705, ffd611, ffb613, ff8b13, ff6e08, ff500d, ff0000, de0101, c21301, a71001, 911003'
};
Map.addLayer(RSEI_imgcol.first().select('rsei'), visParam, 'rsei')