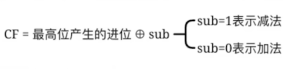上一节提到了
加法的原理其实就是同号绝对值作加法 异号则绝对值大减小 符号同绝对值大的数
减法的原理就是把 减数取反 再做加法
在此基础上 我们先回顾上一节提到的那个加法器的原理图
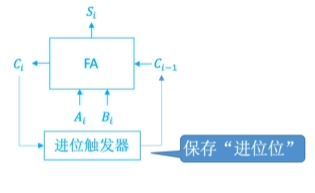
我们都知道 机器字长(也就是一次能够处理的数的位数)是固定的 那一定会有溢出的情况 于是就有了这个 溢出判断
溢出判断
引出

溢出一般分为这样两种 情况

溢出的本质就是
补码无法表示这个数的真实的值了 一种情况是他太大 一种情况是他太小
太大的叫上溢 太小的叫下溢
溢出 说明是不正常的 不正常的也就是违反常理的
什么叫违反常理?正+正=负 负+负=正 这就叫违反常理 没毛病吧?
这一大段话咋一听好像是废话 但实际也确实如此 但后面会用到这个基本的思想
解决办法
我们发现一个问题 就要去解决他 计算机也一定会有他的解决办法来处理这个问题
那计算机是如何判断的呢?
这就要用到上面那句话了 太大的叫上溢 太小的叫下溢
先说上溢
既然是太大 那一定会是两个正数相加 才会大
好既然是两个正数 那我们就看回上面说到的那两句话的第一句“正+正=负”这是个很异常的情况对吧?
那么面向这个结果来判断 :
发生了溢出->结果是负数->结果的符号位是1
那这个符号位的1从哪里来?只能够从最高数值位进位而来!为什么呢?因为两个正数的符号位都是0 两个0大眼瞪小眼死活也凑不出一个1啊!
想明白了这一点 就能轻而易举的想到 但凡发生上溢的情况 必然满足以下规律
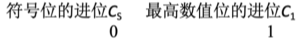
再到下溢
老样子 从事物的本质出发 下溢的本质是太小了->两个负数相加 才会小->异常情况就是违反常理所以负+负=正->结果的符号位是0
也就是说只要发生溢出 结果数符号位必定是0 但是两个负数的符号位已经是1了,他们相加必然 进位,在这种情况下我们要保证什么?保证不能再有1了呀 因为一旦最高数值位进1 原先的1又变成0了
所以就有以下规律:

也就是说只要判断他俩异不异 就能判断是否溢出
计算机用什么来判断一件事的结果?标志。所以标志位就应运而生了
标志位
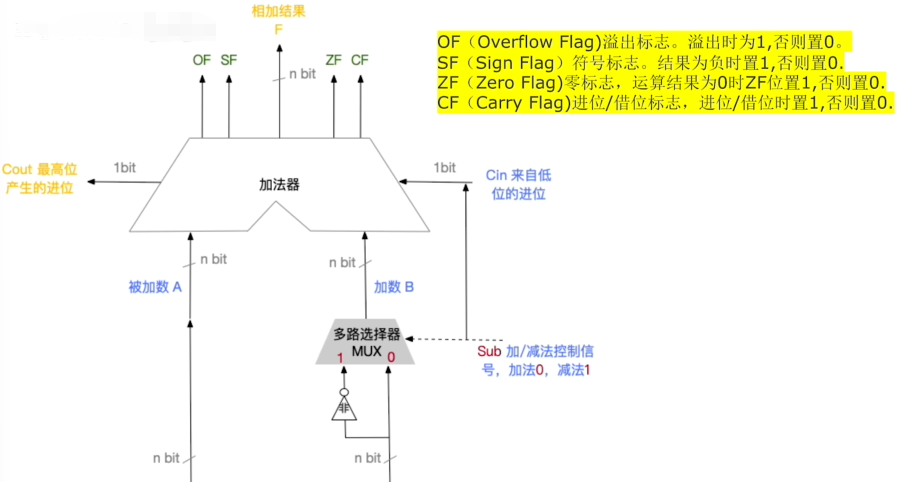
标志位一共有上面那四种 我就不cv了
无非就是督促兄弟们背多几个单词就能记住的事情
那么上面的文章 已经推导了 溢出判断 的过程 所以 OF=Cs异或C1,书上可能会写成小加号的形式
SF ZF 就是字面 意思 用来标记这个数是正是负 是不是0
CF
进位和借位 其实就是无符号数的溢出情况 只是换了种说法
既然确认了对象是无符号数(默认是正数)
sub(加法0减法1)要和最高位数值的进位进行异或
因为当减法的时候 如果最高位没有进1 说明他产生了借位(减法的原理是把减数变为负数的补码 再相加)
而当加法的时候 最高位进了1 说明进位了 按照这个 规律