大家好,又见面了,我是你们的朋友全栈君。
还有一种去体积的方法,往往它比上篇文章的方法更加方便。
为了理解这种方法,考虑图1左边所示的区域,也就是,第一象限数轴和所示示曲线 y=f(x) y=f(x)围成的区域。如果这个区域绕 x x轴旋转,那么图中的垂直窄带生成一个圆盘,我们能够从
x=0
x=0到 x=b x=b区间上积分这些圆盘的体积得到总体积。当然,这是上篇文章中描述的圆盘法。然而,如果区域绕 y y轴旋转,就像图中间的那样,那么我们获得完全不同的物体,垂直窄带产生了很薄的圆柱壳。这个壳可以看做一个罐头,只是其顶部和底部已被去掉,或者很薄的纸板。其体积
dV
dV本质上是内圆柱表面积 (2πxy) (2\pi xy)乘以厚度 (dx) (dx),所以
dV=2πxydx(1)
\begin{equation}dV=2\pi xydx\tag1\end{equation}
这个壳的半径 x x从
x=0
x=0增长到 x=b x=b,从图1可以看出,圆柱壳序列填充沿着轴向外充满了整个物体。因此总体积就是 dV dV体积元的和-或积分
V=∫dV=∫2πxydx=∫b02πxf(x)dx(2)
\begin{equation}V=\int dV=\int 2\pi xydx=\int_0^b2\pi xf(x)dx\tag2\end{equation}
其中 y=f(x) y=f(x),原则上,体积 V V也可以用水平窄带得到的水平圆盘来计算;然而我们会发现这非常困难,因为给定的方程
y=f(x)
y=f(x)无法用 y y来表示
x
x。
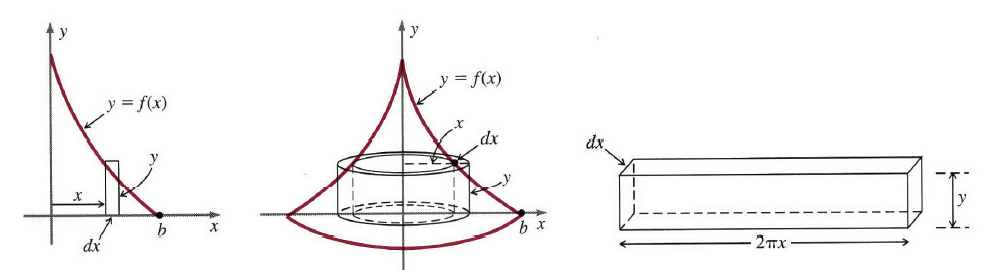
图1
和其他积分的应用一样,等式(1)(2)将涉及到和极限的复杂过程变成简洁的表达式,为了清楚起见,我们忽略这个过程的细节。
还跟之前一样,我们建议大家不要死记公式(2)。这个公式类似于对应的圆盘法公式,如果只是死记而不加思考的话,很容易将他们用混并打字自信。更好地方式是画图,直接从图中可见的信息来构建(1),然后对形式(2)进行积分。此外,这种方法更大的优势,我们不用依赖于任何特定的符号,可以很容易将基本思想应用到各种轴旋转得到的物体上。
例1:上篇文章中我们用圆盘法计算了球体的体积。现在我们用圆柱壳法在此解决这问题(图2)。图中所示壳的体积为
dV=2πx(2y)dx=4πxa2−x2−−−−−−√dx
\begin{align*}dV&=2\pi x(2y)dx\\&=4\pi x\sqrt{a^2-x^2}dx\end{align*}
因此球体的体积是
V=4π∫a0xa2−x2−−−−−−√dx=4π(−13)(a2−x2)3/2∣∣a0=−4π3(a2−x2)3/2∣∣a0=43πa3
\begin{align*}V&=4\pi\int_0^ax\sqrt{a^2-x^2}dx=4\pi (-\frac{1}{3})(a^2-x^2)^{3/2}\Big|_0^a\\&=-\frac{4\pi}{3}(a^2-x^2)^{3/2}\Big|_0^a=\frac{4}{3}\pi a^3\end{align*}

图2
另外,我们考虑一个相关问题:如果一个直径为 a a的垂直洞通过了球中,那么如何找到剩余的体积。为此,显然积分
dV
dV 的区间变成从 x=a/2 x=a/2到 x=a x=a,所以
V=4π∫aa/2xa2−x2−−−−−−√dx=−4π3(a2−x2)3/2∣∣aa/2=43π(34a2)3/2=43π(33√8a3)=3√2πa3
\begin{align*}V&=4\pi\int_{a/2}^ax\sqrt{a^2-x^2}dx=-\frac{4\pi}{3}(a^2-x^2)^{3/2}\Big|_{a/2}^a\\&=\frac{4}{3}\pi\left(\frac{3}{4}a^2\right)^{3/2}=\frac{4}{3}\pi\left(\frac{3\sqrt{3}}{8}a^3\right)=\frac{\sqrt{3}}{2}\pi a^3\end{align*}
这个问题可以用垫圈法解决,不是圆柱壳法更加方便。
例2: y=x2 y=x^2上方和 y=2−x2 y=2-x^2下方在第一象限围成的区域绕 y y轴旋转(图3)。为了用圆柱壳法求出体积,通过观察可以看出壳的高度为
y=(2−x2)−x2=2−2x2
y=(2-x^2)-x^2=2-2x^2,所以
dV=2πxydx=2πx(2−2x2)dx=4πx(x−x3)dx
\begin{align*}dV&=2\pi xydx=2\pi x(2-2x^2)dx\\&=4\pi x(x-x^3)dx\end{align*}
因为曲线交点位于 x=±1 x=\pm 1处,从而
V=4π∫10(x−x3)dx=4π(12x2−14x4)∣∣10=π
\begin{align*}V&=4\pi\int_0^1(x-x^3)dx\\&=4\pi (\frac{1}{2}x^2-\frac{1}{4}x^4)\Big|_0^1=\pi\end{align*}
大家常常错误的积分区域设置为从 x=−1 x=-1到 x=1 x=1。这个不正确的原因可以从几何上理解,圆柱壳横扫从数轴向外横扫物体的半径是从0增加到l,不是从-l增加到1。
注意,如果我们试图用圆盘法解决这个问题,那么它需要计算两个积分-一个是曲线交点下面的体积,另一个是上面的体积。
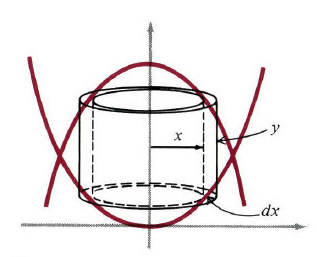
图3
例3:血流量。人类身体主动脉-大动脉-是一个管道,有人类拇指那样大。心脏通过跳动使血液通过动脉,靠近中心的血粒子移动速度约是 50 cm/s(20 in/s) 50\ cm/s(20\ in/s)。另一方面,血液是粘稠的液体,动脉壁附近的血倾向于黏着在血管壁上,所以它的速度基本上为零。在这些情况下计算总流量的问题就需要用圆柱壳法积分得到。
我们用非常简单的想法开始,如果液体以恒定的速度 s0 s_0流经圆柱管,那么单位时间通过一个某处的液体体积(流量F)是 s0A s_0A, A A是血管的截面面积(图4)。
然而,我们知道,人体动脉中血液流动比这复杂得多。我们假设动脉是圆柱形,长度为
L
L半径为 R R(图5)。因为上面提到的粘度,在薄的圆柱内有血液流动,并且每层移动速度大约恒定而不同层的速度不同。这就是所谓的层流流动,血液在靠近动脉壁附近流速慢而中心位置流速快(如图5所示),这样的话内部层滑到了外部的前面(图6)。
速度
s
s和距中心距离 r r之间的确切关系是
s=P4ηL(R2−r2)(3)
\begin{equation}s=\frac{P}{4\eta L}(R^2-r^2)\tag3\end{equation}

图4
其中 P P是动脉之间的压力差,
η
\eta是血液的粘度。我们注意到,如果速度 r=R r=R,那么速度为零;如果 r=0 r=0,那么速度最大为 PR2/4ηL PR^2/4\eta L。通常用厘米 (cm) (cm)来度量 R,r,L R,r,L,用 dynes/cm2 dynes/cm^2来度量 P P,
dyne−s/cm2
dyne-s/cm^2来度量 η \eta,这样的话 cm/s cm/s度量 s s。对于人体而言一般
R=0.2 cm
R=0.2\ cm,常数 P/4ηL P/4\eta L是500。根据这些值(3)变为
s=5000(0.22−r2)=20−500r2cm/s(4)
\begin{align}s&=5000(0.2^2-r^2)\nonumber\\&=20-500r^2\quad cm/s\tag4\end{align}

图5
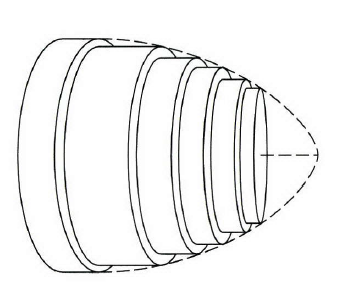
图6
这个函数图像时抛物线的一部分(图7)并且它还说明随着血粒子靠近血管壁,它的速度趋近于零。中心的速度为 20 cm/s 20\ cm/s,但是当 r=0.15 r=0.15时,速度只有 s=20−500(0.15)2=8.75 cm/s s=20-500(0.15)^2=8.75\ cm/s。
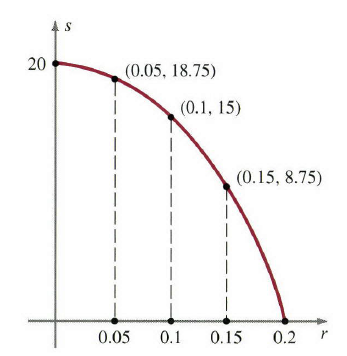
图7
现在,为了计算流量 F F(单位时间通过某处的总体积),我们写出半径为
r
r厚度为 dr dr的圆柱壳的流量元 dF dF:
dF=s⋅2πrdr=P4ηL(R2−r2)⋅2πrdr=πP2ηL(R2r−r3)dr
\begin{align*}dF&=s\cdot 2\pi rdr\\&=\frac{P}{4\eta L}(R^2-r^2)\cdot 2\pi rdr\\&=\frac{\pi P}{2\eta L}(R^2r-r^3)dr\end{align*}
剩下的工作是将所有的壳加起来,即从 0 0到
R
R进行积分:
F=∫dF=∫R0πP2ηL∫R0(R2r−r3)dr=∫R0πP2ηL(12R2r2−14r4)∣∣R0=πP8ηLR4
\begin{align*}F=\int dF&=\int_0^R\frac{\pi P}{2\eta L}\int_0^R(R^2r-r^3)dr\\&=\int_0^R\frac{\pi P}{2\eta L}(\frac{1}{2}R^2r^2-\frac{1}{4}r^4)\Big|_0^R=\frac{\pi P}{8\eta L}R^4\end{align*}
这个公式
F=πP8ηLR4(5)
\begin{equation}F=\frac{\pi P}{8\eta L}R^4\tag5\end{equation}
心血管生理学领域叫做 Poiseuille′s law Poiseuille's\ law。它表明流量与动脉半径的四次方成正比,所以半径增加一倍流量要乘以16。
发布者:全栈程序员栈长,转载请注明出处:https://javaforall.cn/133751.html原文链接:https://javaforall.cn