漫步微积分三十四——体积计算:圆柱壳法
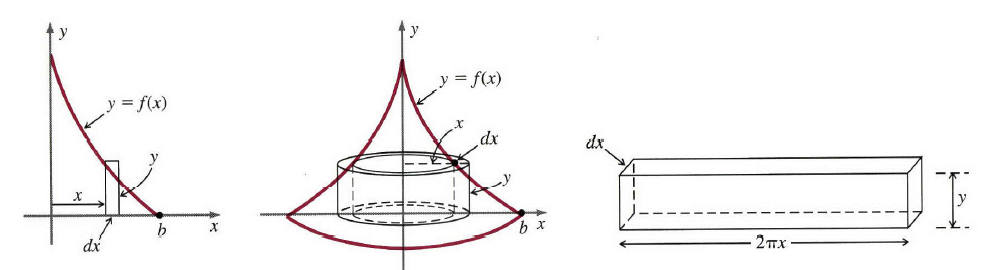
为了理解这种方法,考虑图1左边所示的区域,也就是,第一象限数轴和所示示曲线 y=f(x) y=f(x)围成的区域。如果这个区域绕 x x轴旋转,那么图中的垂直窄带生成一个圆盘,我们能够从
x=0
x=0到 x=b x=b区间上积分这些圆盘的体积得到总体积。当然,这是上篇文章中描述的圆盘法。然而,如果区域绕 y y轴旋转,就像图中间的那样,那么我们获得完全不同的物体,垂直窄带产生了很薄的圆柱壳。这个壳可以看做一个罐头,只是其顶部和底部已被去掉,或者很薄的纸板。其体积
dV
dV本质上是内圆柱表面积 (2πxy) (2\pi xy)乘以厚度 (dx) (dx),所以
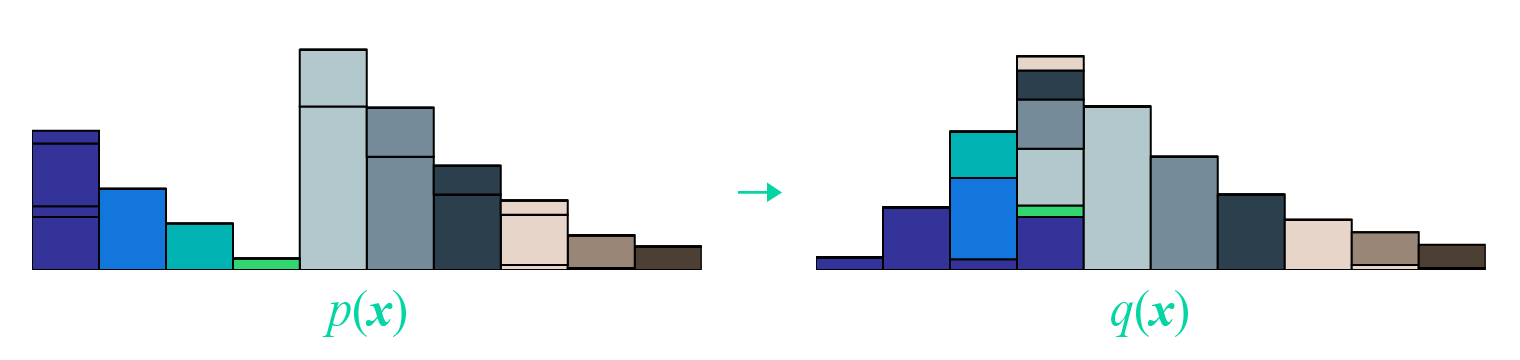
从EMD、WMD、WRD:文本向量序列的相似度计算
在NLP中,我们经常要比较两个句子的相似度,其标准方法是将句子编码为固定大小的向量,然后用某种几何距离(欧氏距离、cos距离等)作为相似度。这种方案相对来说比较简单,而且检索起来比较快速,一定程度上能满足工程需求
漫步微积分三十四——体积计算:圆柱壳法
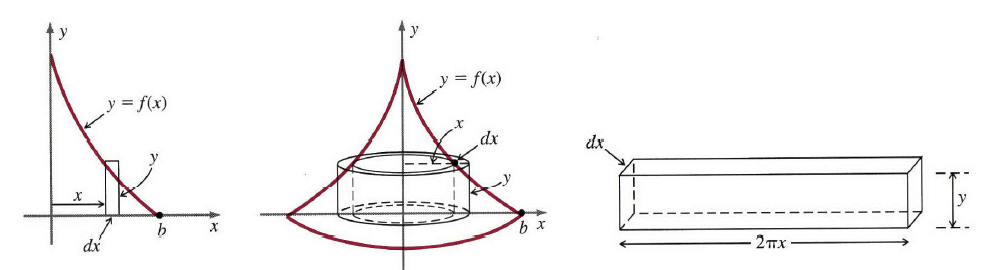
为了理解这种方法,考虑图1左边所示的区域,也就是,第一象限数轴和所示示曲线 y=f(x) y=f(x)围成的区域。如果这个区域绕 x x轴旋转,那么图中的垂直窄带生成一个圆盘,我们能够从
x=0
x=0到 x=b x=b区间上积分这些圆盘的体积得到总体积。当然,这是上篇文章中描述的圆盘法。然而,如果区域绕 y y轴旋转,就像图中间的那样,那么我们获得完全不同的物体,垂直窄带产生了很薄的圆柱壳。这个壳可以看做一个罐头,只是其顶部和底部已被去掉,或者很薄的纸板。其体积
dV
dV本质上是内圆柱表面积 (2πxy) (2\pi xy)乘以厚度 (dx) (dx),所以
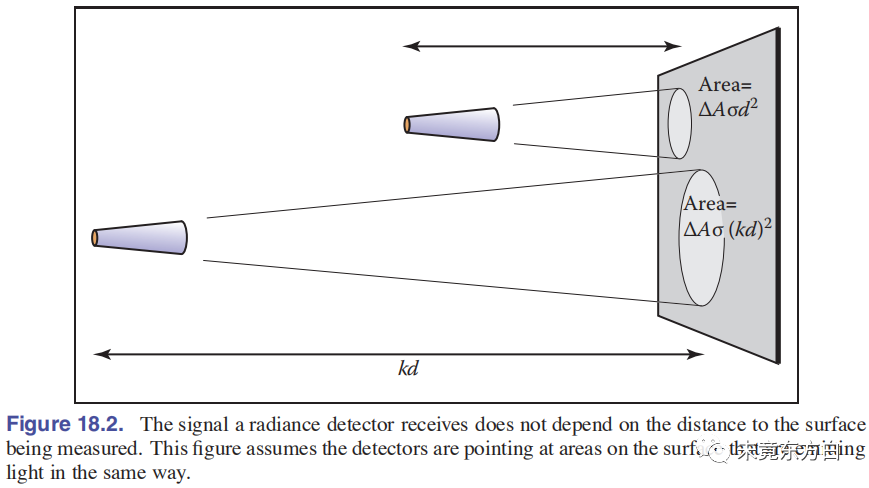
【笔记】《计算机图形学》(18)——光
辐射学, 描述和研究辐射现象运作的学科, 图形学需要用到其描述光线传播的部分. 下面是需要用到的光的一些属性:
python 微积分计算
dsolve函数是用来解决微分方程(differential equation)的函数。