文章目录
- 一、顶点覆盖问题
- 二、哈密顿路径问题
- 三、旅行商问题
- 四、子集和问题
- 五、NP 完全问题
一、顶点覆盖问题
顶点覆盖 ( Vertex Cover ) :
给定一个 无向图
,
的 点集覆盖 定义 :
找到 无向图
的 点集子集
,
使得 无向图
中的任何一条边 , 都与 点集子集
的至少一个节点是接触的 ;
顶点覆盖问题 : 查看 无向图
中 是否包含一个指定大小的 满足上述要求的 点集子集
;
符号化表示 :
其中
个节点 的 点集覆盖 就是无向图中有
个点的点集子集 , 满足点集覆盖要求 ;
点集覆盖 是
完全问题 ;
二、哈密顿路径问题
哈密顿路径问题在图论中是很重要的问题 ;
在下图中 , 从某个顶点出发 , 将所有的顶点都走一遍, 并且每个顶点只能经过一次 ,
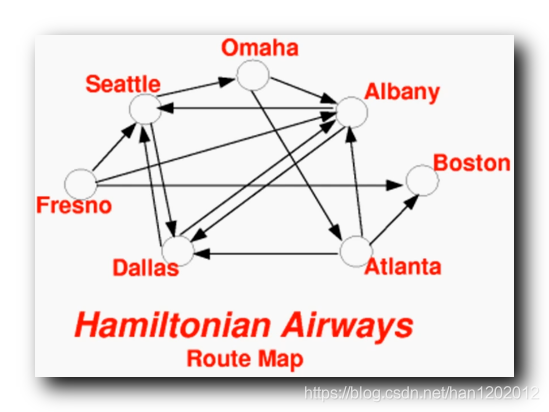
经过所有顶点的 圈 称为 哈密顿圈 ,
经过所有顶点的 道路 称为 哈密顿道路 , 又称为 哈密顿路径 ;
哈密顿路径问题 就是 找到无向图中的哈密顿路径 ;
涉及到的其它概念 : … 途径 : 顶点和边的交替出现的序列 , 其顺序符合图中的位置即可 ; 迹 : 每个边不能相同的 途径 ; 路 : 每个点都不相同的 迹 ; … 这三个概念 , 一个比一个严格 ; … 闭途径 : 起点 和 终点 相同的 途径 ; 闭迹 : 起点 和 终点 相同的 迹 , 也称 回路 ; 圈 : 起点 和 终点 相同的 路 ; …
指的是 Graphic 图 ;
指的是 Edge 边 ;
指的是 Vertext 顶点 ;
哈密顿路径 , 参考 【图论】简单 概念 及 公式 入门 ( 完全图 | 二部图 | 连通图 | 欧拉回路 | 哈密顿圈 | 平面图 | 欧拉定理 ) 博客中的 欧拉回路 与 哈密顿圈 ;
哈密顿路径问题 是
完全的 ;
无向图中哈密顿路径是否存在 , 该问题也是
完全的 ;
前者是求出具体的哈密顿路径 , 后者求哈密顿路径是否存在 ;
三、旅行商问题
旅行商问题 : 无向图中 , 每条边都有一个权重 , 求是否有一条哈密顿路径的权重之和 , 不超过给定的自然数
;
旅行商问题 是
完全的 ;
四、子集和问题
子集和问题 : 给定一个 自然数集合 , 给定一个 自然数
, 问给定的自然数集合中 , 是否存在子集 , 使它们之和等于给定的自然数
;
子集和问题 是
完全的 ;
五、NP 完全问题
计算理论中的
完全问题 :
布尔可满足性问题 ;
哈密顿路径问题 ;
旅行商问题 ;
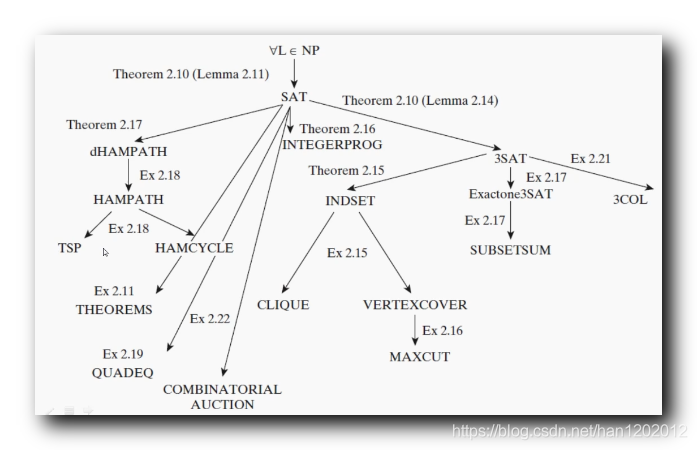
下图就是已知的
完全问题 ;