【计算理论】计算复杂性 ( 非确定性图灵机的时间复杂度 | 非确定性图灵机 与 确定性图灵机 的时间复杂度 之间的关系 )
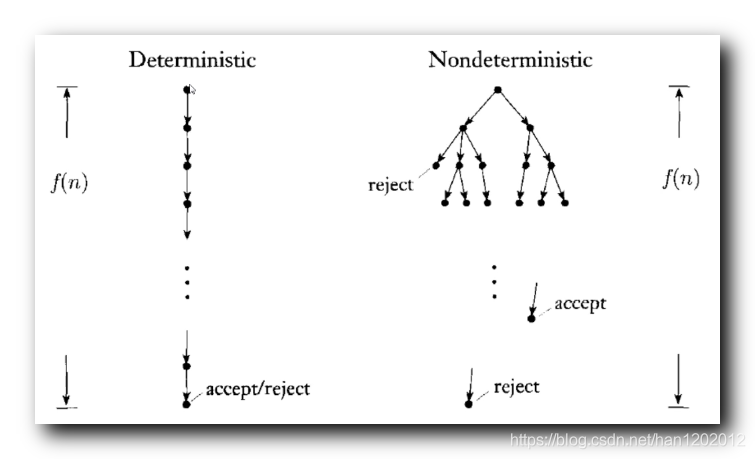
给定一个非确定性图灵机 , 该图灵机是 判定机 , 在所有的输入上都会停机 , 肯定能得到一个 接受状态 或 拒绝状态 结果 ;
【腾讯云 Cloud Studio 实战训练营】Hexo 框架 Butterfly 主题搭建个人博客
随着信息技术的快速发展,互联网已经成为了获取知识、分享见解以及展示个人能力的重要平台之一。在这个数字化时代,越来越多的开发者和技术爱好者选择通过建立自己的技术博客来展示他们的专业知识和独特观点。技术博客不仅可以帮助你记录学习的过程,还可以让你与全球范围内的开发者社区互动,获得反馈和建议,进一步提升自己的技能水平。
WordPress 博客使用腾讯云对象存储 COS 进行静态资源 CDN 加速
WPJAM Basic 最新版已经实现了对腾讯云 COS WebP 功能的支持,开启之后,可以大大节省 CDN 费用。

白嫖可道云静态文件CDN,给自建站点加速
获取可道云静态文件CDN链接
通过F12+演示站获取,获取到的链接如下(2020-09-17):
https://static.kodcloud.com/kod/static/last/
修改可道云配置文件
配置文件路径./config/setting_user.php
打开文件,在文件末尾添加如下内容:
$GLOBALS['config']['settings']['staticPath'] = "https://static.kodcloud.com/kod/static/last/";
----
记录
白嫖可道云静态文件CDN,给自建站点加速
获取可道云静态文件CDN链接
通过F12+演示站获取,获取到的链接如下(2020-09-17):
https://static.kodcloud.com/kod/static/last/
修改可道云配置文件
配置文件路径./config/setting_user.php
打开文件,在文件末尾添加如下内容:
$GLOBALS['config']['settings']['staticPath'] = "https://static.kodcloud.com/kod/static/last/";
----
记录
还记得当初为什么选择计算机?我的代码人生旅程
在这篇博客中,我将探讨计算机科学的魅力、编程的乐趣和技术对个人成长的影响。文章内容丰富,涵盖了编程基础、技术趋势、程序开发实战经验等,旨在为不同层次的读者提供价值。关键词包括:编程入门、技术趋势、计算机科学、个人成长、程序开发。

【BLE MIDI】MIDI 时间标志分析 ( 音符速度设置事件 | 拍号设置事件 | 基本时间 - 每个四分音符有多少 tick 或 pulse | 节拍时值计算 | 小节时值计算 )
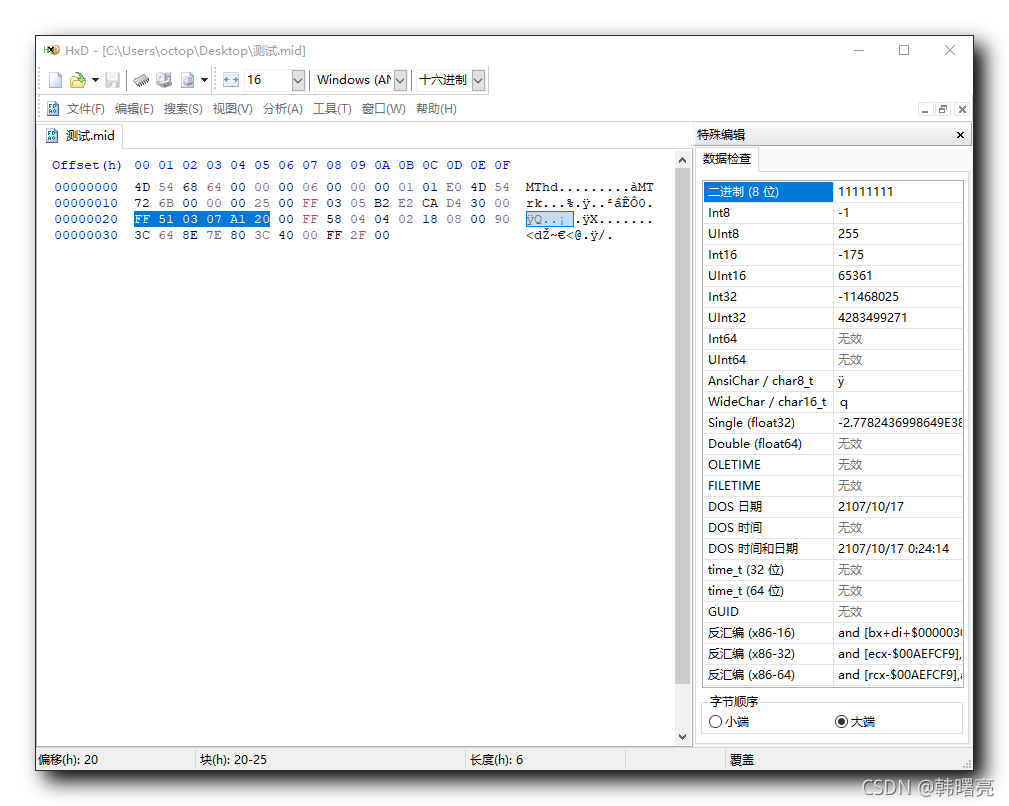
MIDI 文件中的 " 音符速度设置 Meta 事件 " , " 拍号设置 Meta 事件 " , " 文件头的 基本时间 " , 决定了该 MIDI 曲子的事件标志 ;
【云+社区年度征文】2020年年终总结
俗话常说:老鼠过街,人人喊打。鼠年,好像一直都是不太平的:今年,新冠病毒;08年,汶川大地震……大家都在叫唤今年的日子不好过,可不管好不好过时间不会因为日子是否好过而停止,这不转眼间“不太好过”的今年已经快结束了。趁着这个周末,盘点一下今年的方方面面,对今年做一个总结。
沉醉于代码的境界:探寻计算机书籍的奇妙之旅
计算机书籍,如同一扇通向代码世界的大门,吸引着无数程序员和技术爱好者。每一本书都是一个知识的宝库,蕴含着作者的智慧和经验。曾经,我也深陷于一本计算机书籍之中,读得如痴如醉,仿佛置身于一个无尽的代码世界。让我分享一下那段沉迷于书籍的时光,以及书籍带给我的启示。
【CSS】CSS 特性 ③ ( CSS 优先级 | 权重叠加计算公式 )
在使用 多个类型的 基础选择器 进行 组合 时 , 如 交集选择器 / 后代选择器 等 , 涉及到将 多个 基础选择器 的 权重进行叠加 ;
【C语言】库宏offsetof(结构体成员偏移量计算宏)
如下,我们使用offsetof打印一下结构体foo中,成员a,成员b及成员c相对于首地址的偏移量分别是多少:

沉醉于代码的境界:探寻计算机书籍的奇妙之旅
计算机书籍,如同一扇通向代码世界的大门,吸引着无数程序员和技术爱好者。每一本书都是一个知识的宝库,蕴含着作者的智慧和经验。曾经,我也深陷于一本计算机书籍之中,读得如痴如醉,仿佛置身于一个无尽的代码世界。让我分享一下那段沉迷于书籍的时光,以及书籍带给我的启示。
【计算理论】计算复杂性 ( 两个带子的图灵机的时间复杂度 | 证明多个带子图灵机时间复杂度 )
示例 : 参考上一篇博客 【计算理论】计算复杂性 ( 两个带子的图灵机的时间复杂度 ) , 识别语言

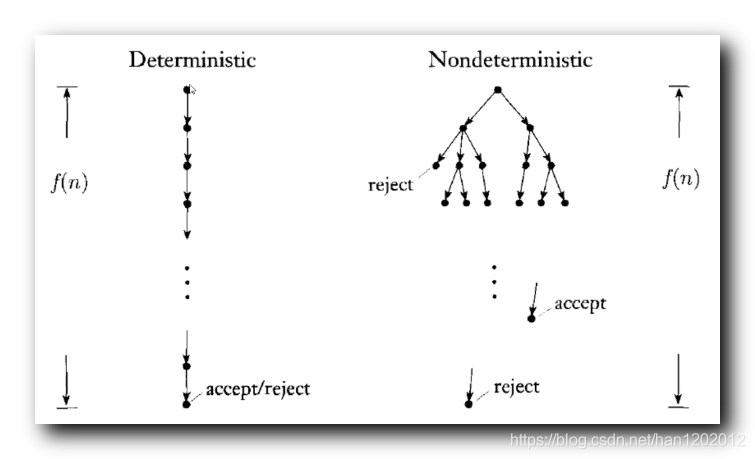
【计算理论】计算复杂性 ( 证明 非确定性图灵机 与 确定性图灵机 的时间复杂度 之间的指数关系 )
在上一篇博客 【计算理论】计算复杂性 ( 非确定性图灵机的时间复杂度 | 非确定性图灵机 与 确定性图灵机 的时间复杂度 之间的关系 ) 中 , 提出如下命题 :
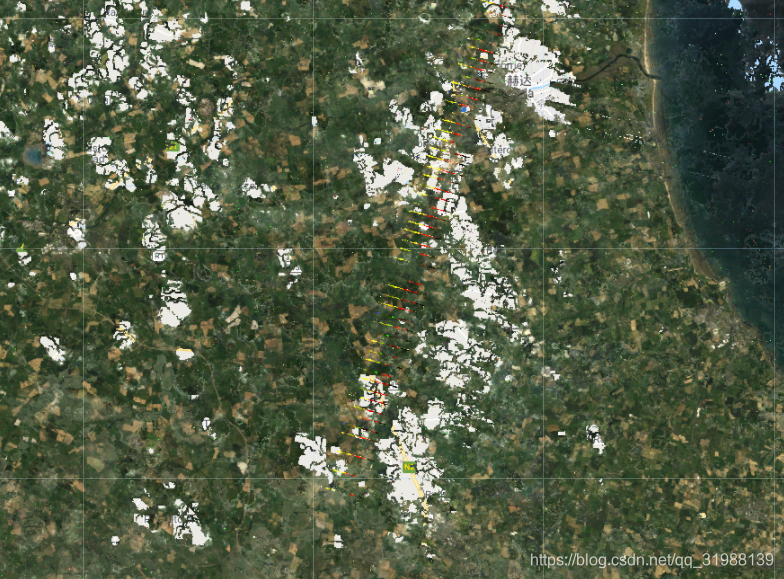
Google Earth Engine(GEE)——Landsat4/5/7 SR数据除云
Landsat4/5/7 SR数据除云是我们进行波段计算必须要进行的一项工作,这样能更加准确的获取波段信息,所以我们今天来简单介绍除云。当然除云后会有空白板块的出现,这是在所难免的,至于影像色差如何取补,可以点击连接访问:
在云服务器上安装Docker-CSDN博客
本文采用华为云云耀云服务器L实例,购买云耀云服务器L实例详见上一篇文章华为云云耀云服务器 L 实例评测 |云服务器选购。
git 把项目托管到 码云出现的错误集合
https://blog.csdn.net/weixin_49931650/article/details/132416285?spm=1001.2014.3001.5501

【Linux 内核】CFS 调度器 ③ ( 计算进程 “ 虚拟运行时间 “ )
在上一篇博客 【Linux 内核】CFS 调度器 ② ( CFS 调度器 “ 权重 “ 概念 | CFS 调度器调度实例 | 计算进程 “ 实际运行时间 “ ) 中 , 计算了 进程 在 CPU 上的 " 实际运行时间 " , CPU 的总时间是 CPU 的调度区 大小 , 则 进程 在 CPU 上执行的进程 可获取到的 CPU 时间 计算公式如下 :
【计算理论】计算复杂性 ( NP 完全问题 - 布尔可满足性问题 ★ | 布尔可满足性问题是 NP 完全问题证明思路 ) ★
布尔可满足性问题 ( Boolean Satisfiability Problem , SAT ) , 是历史已经找到了一个

Git 安装、配置并把项目托管到码云 Gitee
https://blog.csdn.net/weixin_49931650/article/details/132460492