【计算理论】计算复杂性 ( NP 完全问题 - 布尔可满足性问题 ★ | 布尔可满足性问题是 NP 完全问题证明思路 ) ★

发布于

文章目录

  • 一、NP 完全问题 - 布尔可满足性问题 ★
  • 二、布尔可满足性问题是 NP 完全问题证明思路

一、NP 完全问题 - 布尔可满足性问题 ★

布尔可满足性问题 ( Boolean Satisfiability Problem , SAT ) , 是历史已经找到了一个

\rm NP

完全问题 ;

布尔逻辑公式 : 原子命题变元

\rm x , y , \cdots

通过 联结词 合取

\land

, 析取

\lor

, 否定

\lnot

, 将这些变元联结在一起 , 得到一个布尔逻辑公式 ;

参考 离散数学 - 数据逻辑 - 命题与联结词 博客 : 【数理逻辑】命题和联结词 ( 命题 | 命题符号化 | 真值联结词 | 否 | 合取 | 析取 | 非真值联结词 | 蕴涵 | 等价 )

布尔逻辑公式可满足 , 指的是 存在一个赋值 , 该赋值是从原始命题到真和假的映射 , 是语法到语义的纽带 , 该赋值使得布尔逻辑公式取值为真 , 则称该 布尔逻辑公式可满足 ;

存在一个赋值 , 使得布尔逻辑公式为真 , 该布尔逻辑公式就是可满足的 ;

将 所有 可满足的布尔逻辑公式 , 放在一起 , 组成一个整体 , 称为 布尔可满足性问题 ( Boolean Satisfiability Problem , SAT ) ;

布尔可满足性问题 是

\rm NP

完全的 ;

二、布尔可满足性问题是 NP 完全问题证明思路

布尔可满足性问题是 NP 完全问题证明思路 :

① 首先证明 布尔可满足性问题 是

\rm NP

问题 ;

证明该步骤 , 只需要验证 , 给定布尔逻辑公式 , 给定一个赋值 , 验证该公式在该赋值的情况下 , 取值为真即可 ;

验证过程所花的时间与联结词个数有关 , 联结词的个数 , 肯定布会超过布尔逻辑公式的长度 ,

验证所花费的时间一定是 多项式时间 ,

因此 布尔可满足性问题 在

\rm NP

中 ;

② 再证明 布尔可满足性问题

\rm SAT

是最难的

\rm NP

问题 ;

将 布尔可满足性问题 与

\rm NP

中每个计算问题 进行比较 ,

证明

\rm NP

中的任何计算问题 , 其难易程度 , 布会超过 布尔可满足性问题 ,

即

\rm NP

中的任何计算问题 , 都可以在 多项式时间规约到

\rm SAT

, 即

\rm \leq SAT

,

该证明是很难的 ;

从

\rm NP

中 任选一个计算问题

\rm A

,

\rm A

是

\rm NP

的 , 一定存在一个 非确定性图灵机 可以判定 ( 解决 ) 该问题 , 该 非确定性图灵机 的计算复杂度一定是个多项式

\rm O(n^k)

,

证明该问题

\rm A

一定可以在 多项式时间规约到

\rm SAT

, 符号化表示 :

\rm A \leq SAT

,

给定一个 字符串

\rm w

, 可以被 非确定性图灵机

\rm N

接受 , 从 字符串

\rm w

和 非确定性图灵机

\rm N

出发 , 在 多项式时间 内构造出一个逻辑公式 ,

非确定性图灵机

\rm N

接受 字符串

\rm w

, 当且仅当 构造出的逻辑公式是可满足的 ;

构造该逻辑公式 :

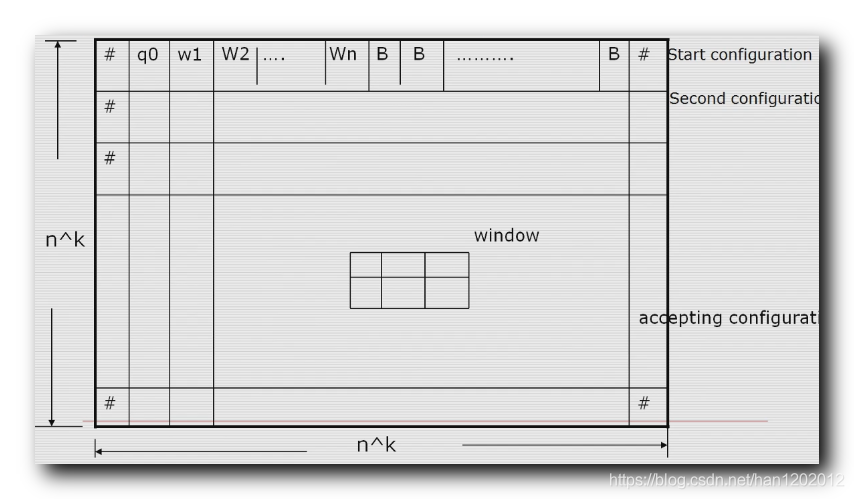
构造如下表格 , 将整个 非确定性图灵机

\rm N

在字符串上作一个计算 , 计算的分支 , 通过一个表格装进去 ;

表格的 长和宽 都是

\rm n^k

,

使用 布尔逻辑公式 表达该表格 , 使得它可以满足一定的条件 ;

在这里插入图片描述

引入如下概念 :

引入字符集 :

\rm N

是非确定性图灵机 , 其中

\rm Q

是

\rm N

的状态集 ,

\Gamma

( 伽马 ) 是

\rm N

的带子的字符集 , 则有 字符集

\rm C = Q \cup \Gamma \cup \{ \# \}

;

引入原子命题变元 :

\rm x_{i,j,s}

, 其中

\rm i , j

都是

\rm [1, n^k]

区间内的值 , 每个

\rm s

都是 字符集

\rm C

中的字符 ;

上述

\rm x_{ijs}

变元的含义是 , 如果该命题变元

\rm x_{ijs}

取值为真 , 当且仅当

\rm i,j

格子 ( 水平为

\rm i

, 垂直为

\rm j

的格子 Cell ) 对应的字符是

\rm s

;

得到布尔逻辑公式 : 上述表格中的格子中 , 任何格子 , 只包含一个字符 , 并且只能包含一个字符 , 该公式的长度是多项式长度 ; 公式如下 :

\rm \phi_{cell} =\begin{matrix} \land \\ \rm 1 \leq i,j \leq n^k \end{matrix} [ ( \begin{matrix}\rm \lor \\ \rm s \in C \end{matrix} x_{i,j,s}) \land ( \begin{matrix}\rm \lor \\ \rm s , t \in C \\ \rm s \not= t \end{matrix} (\lnot x_{i,j,s} \lor \lnot x_{i,j,t} ) ) ]

开始格局 : 表格中的第一行是 开始格局 , 在所有的表格中 , 一定包含了一个接受格局 , 其中一定包含了有一个状态 , 是接受状态 ;

\rm \phi_{start} = x_{1,1,\#} \land x_{1,2,q_0} \land x_{1,3,w_1} \land \cdots \land x_{1 , n+2 , w_n}\land x_{1 , n^k-1 , B} \land x_{1 , n^k , \#}
\rm \phi_{accept} = \lor _{1 \leq i,j \leq n^k} x_{i,j, q_{accept}}

转换函数 : 存在一个

\rm 2 \times 3

的窗口 , 如果是合法的话 , 该表格中的内容 , 刚好是 非确定性图灵机 的 计算树 中的计算分支内容 ;

\rm \phi_{move} = \begin{matrix}\rm \bigwedge \\ \rm 1 < i \leq n^k \\ \rm 1 < j < n^k \end{matrix} \ \ \ ( 窗口 \ (i , j) \ 是合法的 )
\rm \begin{matrix}\rm \bigvee \\ \rm a_1 , \cdots , a_6 \\ \rm legal \\ \rm window \end{matrix} = ( x_{i, j-1, a_1} \land x_{i, j, a_2} \land x_{i, j+1, a_3} \land x_{i +1, j-1, a_4} \land x_{i + 1, j, a_5} \land x_{i + 1, j + 1, a_6} )

合并命题公式集合 : 将上述构造出的所有的命题公式 , 放在一起 , 就得到如下公式 :

\rm \phi = \phi_{cell} \land \phi_{start} \land \phi_{accept} \land \phi_{move}
\rm \phi

的长度是 多项式长度 ,

可以将

\rm NP

中的任何计算问题 在 多项式时间中规约到

\rm SAT

问题 ( 布尔可满足性问题 ) , 布尔可满足性问题 是

\rm P

中最难的问题 , 因此该问题是

\rm NP

完全问题 ;

#表格#博客#函数#语法#字符串