中缀式转后缀式并计算(图文解释
前言:此类笔记仅用于个人复习,内容主要在于记录和体现个人理解,详细还请结合bite课件、录播、板书和代码。
[toc]
前言:用到的头文件
#include<iostream> #include<vector> #include<stack> #include<string> #include<sstream>//stringstream类需要包含的头文件,这个类的作用是将元素全是数字字符string类转换成字面上等价的int类
using namespace std;
1.输入一个中缀式
计算结果就是17(一会儿可以用来验证程序结果是否正确
输入的这个中缀式的数据是由字符组成的,中缀式本身就是一个string类型
如果用字符的话,单个的数字或者符号,比如其中的 ‘5’、’’、’3’、’(‘ 等轻易就会识别出来
但是“12”和“++”就会被识别成’1’、’2’、和’+’、’+’
所以需要将中缀式进行转化,变成能识别多个字符的格式
2.将中缀式变成一个string类型数组,存储的数据由字符变成string类型
建立一个string类型数组,命名为==save==
转化规则:
用一个指针遍历 原中缀式
如果遇到了数字字符,就向后检查,直到遇到非数字字符,将检查的这一段字符都作为一个string的成员保存,并存在==save==中
否则如果遇到了 ‘+’ 或者 ‘-’ ,就向后检查,直到遇到非 ‘+’ 或者 ‘-’ ,将检查的这一段字符都作为一个string的成员保存,并存在==save==中
直到指针遍历完原中缀式为止
vector<string> init(string s) //初始化给出的原始中缀式,处理多位数以及自增自减(原来的中缀式式一个字符串单个元素是一个字符,现在将它初始化为一个容器,容器元素就是字符串(string)
//无论字符有几个都当作一个string并存到vector容器中作为其一个元素
{
vector<string> v;
int i = 0, j;
while (i < s.size())
{
j = i;
if (j < s.size() && s.at(j) <= '9' && s.at(j) >= '0')
{
while (j < s.size() && s.at(j) <= '9' && s.at(j) >= '0') //判断是否为数字以及是不是多位数
j++;
}
else
{
while (j < s.size() && (s.at(j) == '+' || s.at(j) == '-')) //判断是不是自增自减运算符
j++;
}if (i == j) //说明没有遇到数字或者自增自减运算符 v.push_back(s.substr(i++, 1)); else { v.push_back(s.substr(i, j - i)); i = j; } } return v;
}



save就是转化后的中缀式,返回它就可以
3.中缀式转后缀式
用一个string指针遍历中缀式
建立一个字符串数组save,用来存储后缀式的元素
建立一个操作符栈result(string类),用来调整操作符的顺序
规则:
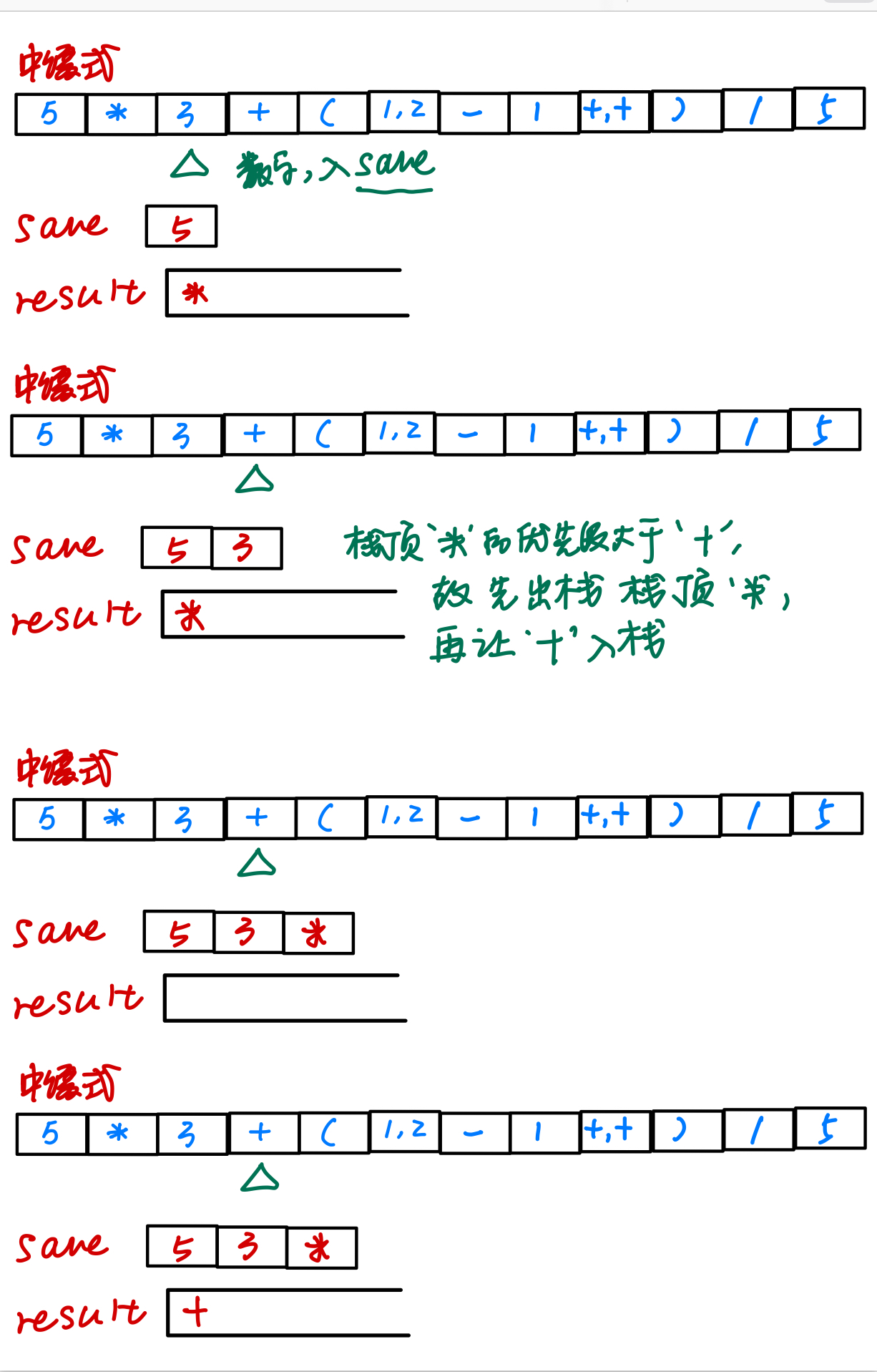
如果元素是数字,就直接进入后缀式
如果元素是操作符,就要进行一下判断:
如果操作符栈result是空的,就直接让元素进栈
如果result栈不是空,就进行判断:
如果栈顶优先度小于中缀式中的,中缀式中的操作符直接进栈
如果栈顶优先度不小于中缀式,则栈顶先出栈到后缀式,中缀式的操作符再进栈
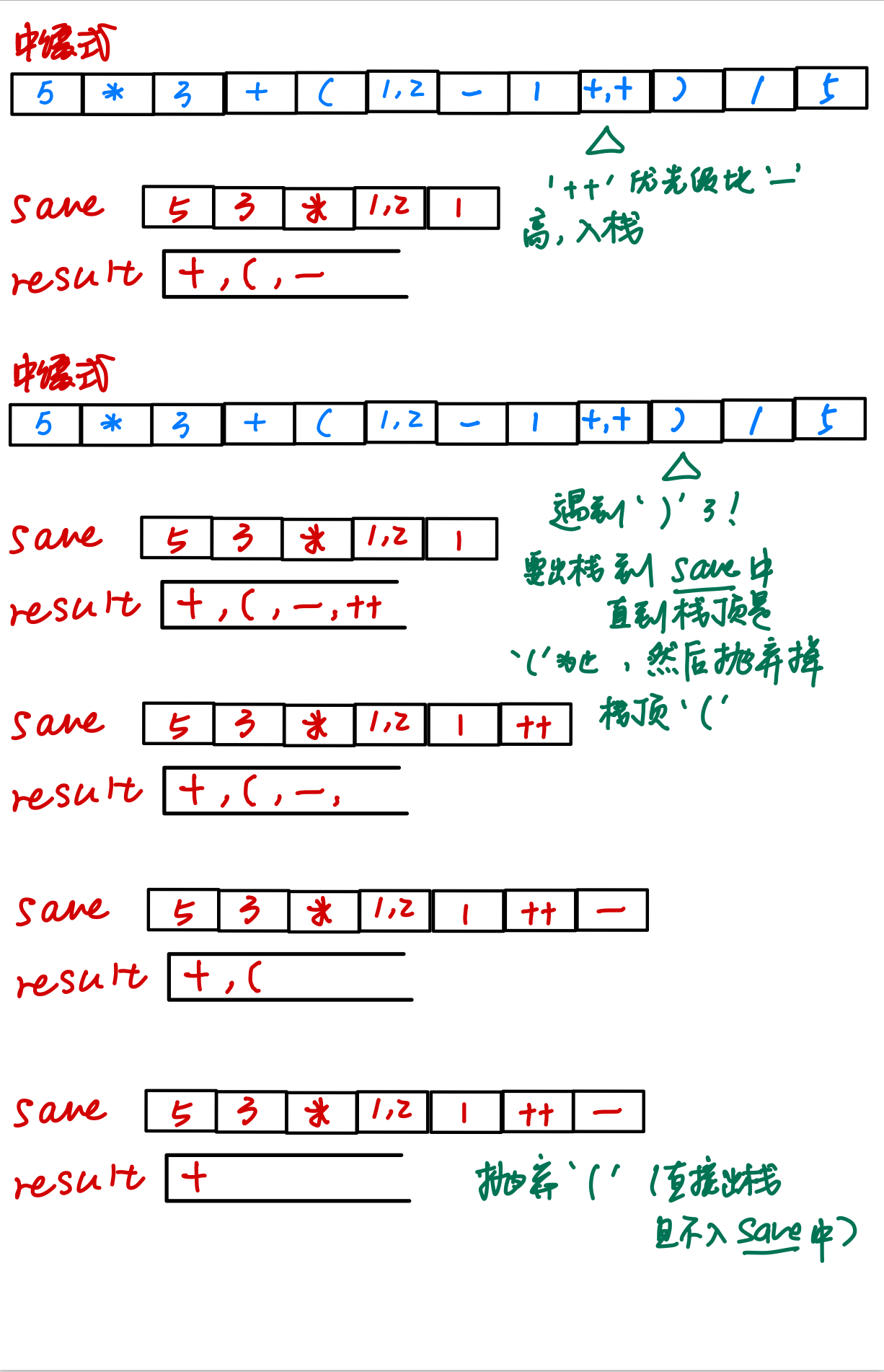
如果中缀式元素是‘)’,则一直出栈,直到把括号内的元素全部出栈
另外,如果‘(’不在栈内,则它的优先度被认为是最高的,栈内的‘(’是最低的
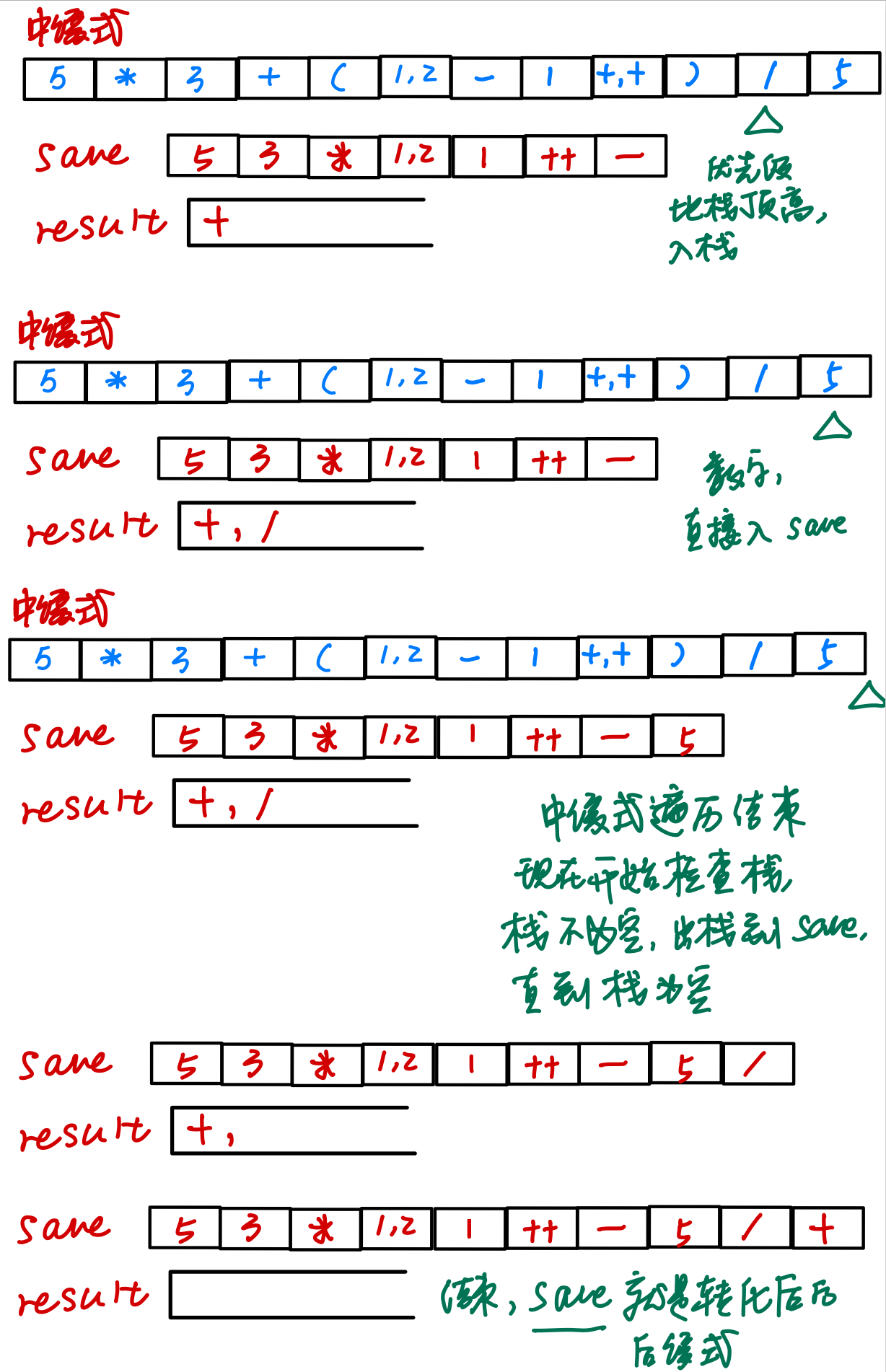
等中缀式遍历完之后,检查栈是否为空,不为空就出栈到后缀式,直到栈为空
操作符优先级:(从上到下递减)
栈外的‘(’
‘++’、‘–‘
’‘、’/‘
’+‘、’-‘
栈内的’(‘
int judge(string s) //判断运算符优先度
{
if (s == "+" || s == "-") //操作符也是string,妙
return 1;
else if (s == "" || s == "/")
return 2;
else if (s == "++" || s == "--") //自增自减优先级是仅次于左括号的
return 3;
else if (s == "(")
return 4;
else if (s == ")")
return -1;
else
return 0;
}vector<string> transform(vector<string> v)//转后缀式
{
stack<string> result;
vector<string> save;
for (int i = 0; i < v.size(); i++)
{if (judge(v[i]) == 0) //遇到数字就直接输出 save.push_back(v[i]); else if (judge(v[i]) > 0) { if (result.empty()) //栈为空则直接压栈 result.push(v[i]); else { if (judge(v[i]) > judge(result.top())) //操作符优先级比栈顶操作符优先级高 { result.push(v[i]); } else { while ((!result.empty()) && judge(result.top()) >= judge(v[i]) && result.top() != "(") //弹栈并输出直到栈为空或遇到优先级更低的操作符 (除了左括号) { save.push_back(result.top()); result.pop(); } result.push(v[i]); } } } else if (judge(v[i]) == -1) { while (result.top() != "(") { save.push_back(result.top()); result.pop(); } result.pop();//抛弃‘(’ } } while (!result.empty()) { save.push_back(result.top()); result.pop(); } return save;
}


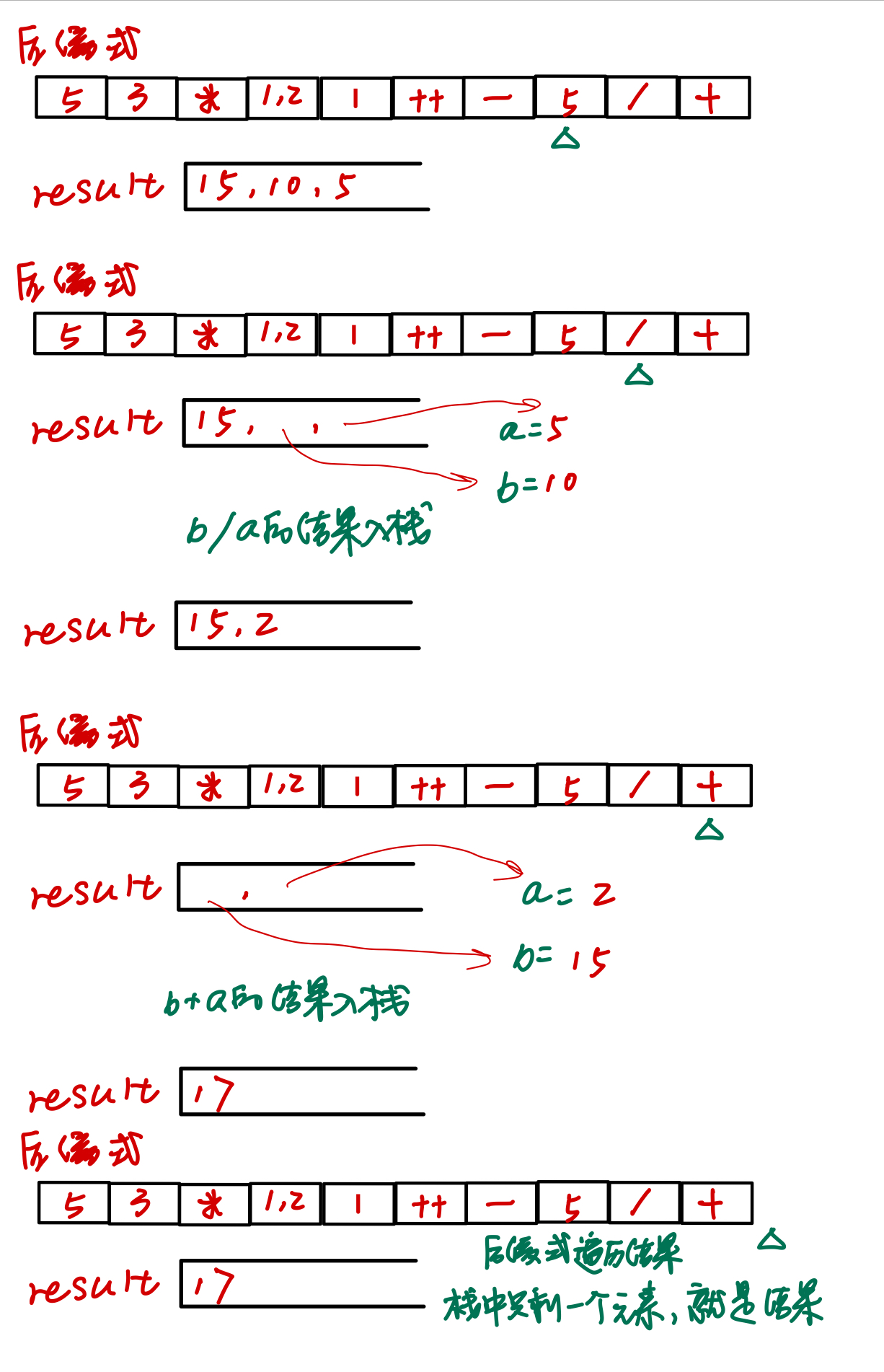
4.后缀式的计算
构建一个计算结果栈,result(int类)
分为两个模块:
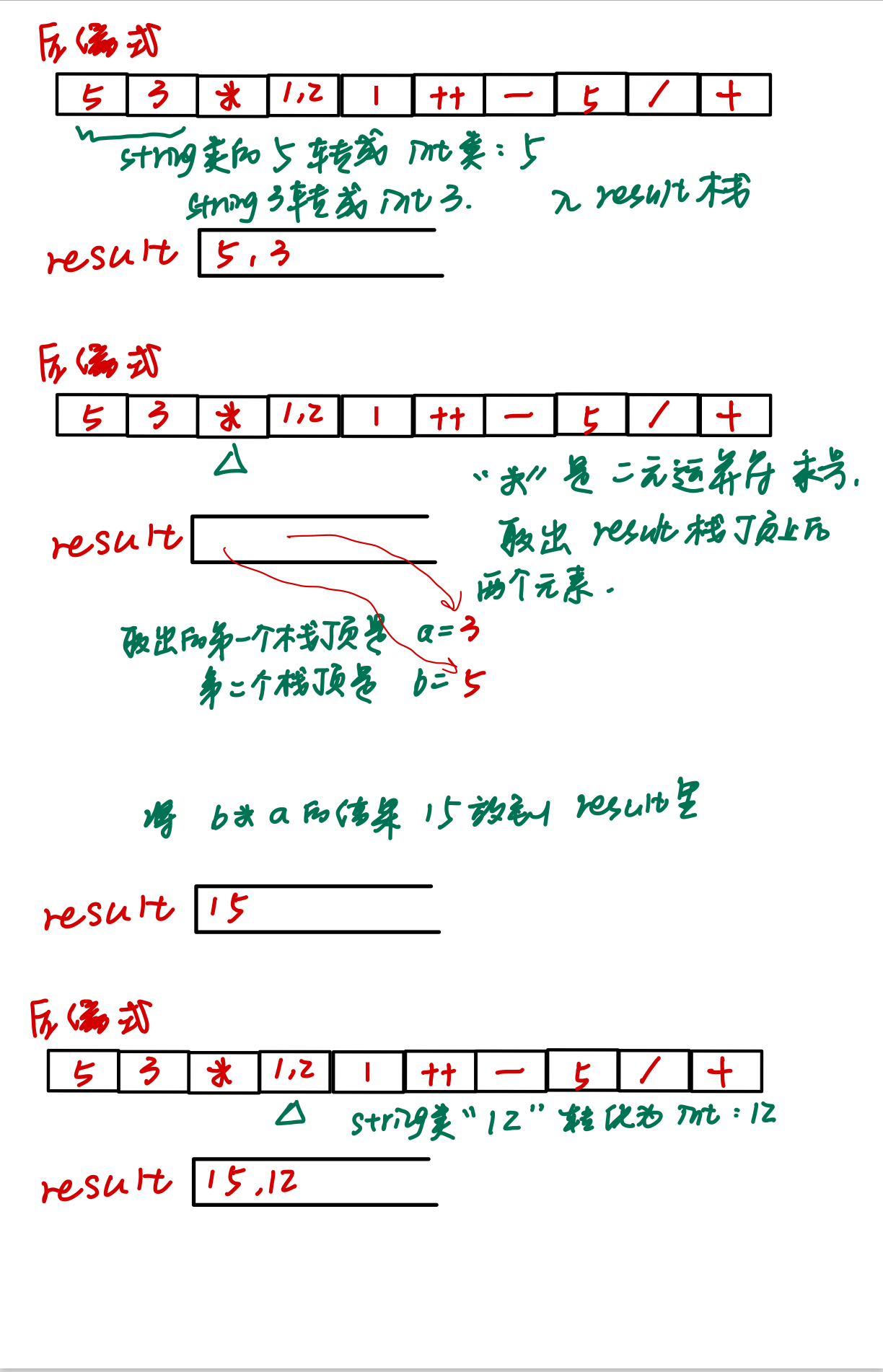
- 如果元素是数字,就进行“string转int”操作,转换后的结果入result栈
- 如果是操作符,就从栈顶取数字进行计算,并将计算结果入result
- 如果操作符是加减乘除,需要从栈中取两个数字,因为加减乘除是二元运算符,另外注意,由于从后缀式入栈到result,先进的数字a在栈底,后进的b在栈顶,而加减乘除是后缀式从前往后的顺序,比如后缀式ab-,ab进栈之后就变成了ba,应该用a-b,而不是b-a
- 如果操作符是一元运算符,就直接取栈顶元素,计算之后返回result
int stringToInt(string s) //将操作数字符串转变成int { stringstream ss;//stringstream类的作用是将元素全是数字字符string类转换成字面上等价的int类 int i; ss << s; ss >> i; return i; }int calculate(vector<string> v) //进行计算
{
stack<int> result; //结果栈
int a, b;for (int i = 0; i < v.size(); i++) { if (judge(v[i]) == 0) //如果是操作数,则转换为int之后直接入到结果栈 result.push(stringToInt(v[i])); else { a = result.top(); result.pop(); if (!result.empty()) //如果结果栈里面的元素够两个的话,才能进行加减乘除 { if (v[i] == "+") { b = result.top(); result.pop(); result.push(b + a); } else if (v[i] == "-") { b = result.top(); result.pop(); result.push(b - a); //因为在后缀式中靠前的元素先入栈,后面的元素后入栈,后入栈的先出,所以在后缀式中的顺序是b在a之前,按照运算顺序就是b-a } else if (v[i] == "*") { b = result.top(); result.pop(); result.push(b * a); } else if (v[i] == "/") { b = result.top(); result.pop(); result.push(b / a); } } if (v[i] == "++") result.push(++a); else if (v[i] == "--") result.push(--a); } } return result.top();
}

5.总的对外接口函数
void InfixToPostfixAndCalculate(string Infix)//总的对外接口
{
cout << "您输入的中缀式是:" << Infix << endl;
vector<string> v1 = init(Infix);//中缀式初始化:将中缀式的元素由字符变成string,将中缀式由string变成vector
vector<string> v2 = transform(v1);//中缀式转后缀式
cout << "转化为后缀式并进行计算的计算结果是:" << calculate(v2) << endl;
}
6.思维导图
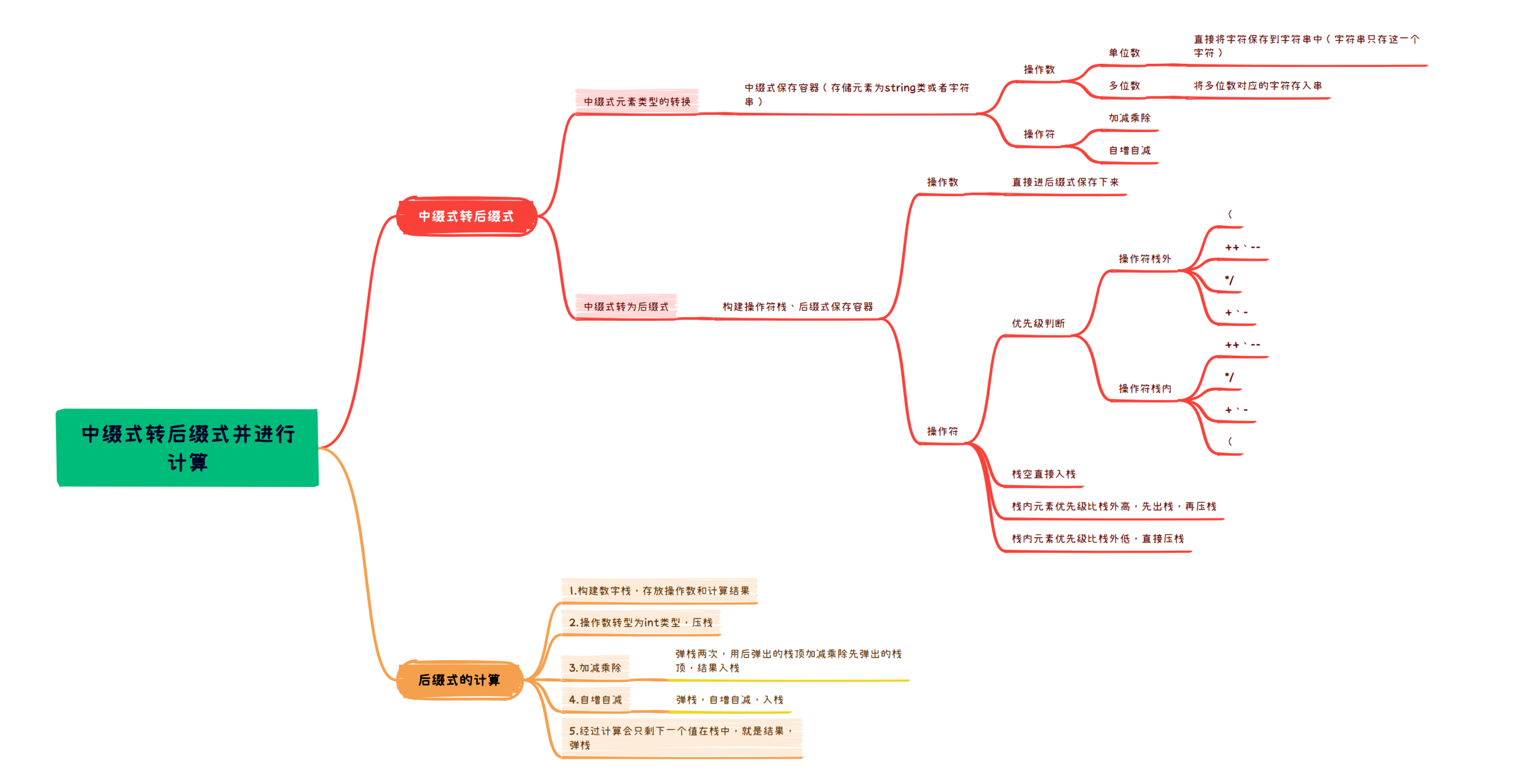
中缀式转后缀式.pdf
7.结束
That’s all, thanks for reading!💐