【计算理论】正则语言 ( 正则语言运算 | 正则语言封闭性 )

发布于

文章目录

  • 一、正则语言引入
  • 二、正则语言
  • 三、 正则语言运算 ★
  • 四、语言运算示例 ★
  • 五、正则语言封闭性 ★
  • 六、正则语言封闭性
A \cup B

证明

  • 七、正则语言封闭性
A \circ B

证明

  • 八、正则语言封闭性
A^*

证明

  • 九、自动机扩展

一、正则语言引入

1 . 非确定性有限自动机 作用 : 非确定性有限自动机并没有增加 自动机 的计算能力 , 但是给自动机设计带来很多方便 ; 仅限于在理论计算时带来很多方便 , 但是无法实现 ;

2 . 自动机实现 : 非确定性有限自动机 ( NFA ) 的的优点是给自动机的设计带来了很多方便 , 但是 只有 确定性的有限自动机 ( DFA ) 才能被实现出来 ;

3 . 自动机等价 : 通过算法可以判定两个确定性的有限自动机是等价的 ,

4 . 自动机优化 : 给定确定性有限自动机 , 可以将该自动机优化 , 得到一个最小的与该 DFA 等价的 自动机 ;

5 . 自动机涉及的两个问题 :

① 优化问题 : 给定一个自动机 , 如何找到一个算法 , 将自动机最小化 ;

② 设计自动机 : 给定一个语言 , 如何找到一个算法 , 根据该语言设计出自动机 ;

6 . 引入正则语言 : 确定性有限自动机 ( DFA ) 与 非确定性有限自动机 ( NFA ) 接受的是相同的语言 , 这个语言就是正则语言 ;

二、正则语言

正则语言 : 如果一个语言 存在一个 有限自动机识别 , 那么称该语言是 正则语言 ;

( 这个自动机可以是 确定性有限自动机 , 也可以是 非确定性有限自动机 ; )

设计自动机 :

① 自动机设计要求 : 给定一个语言 , 设计能识别该语言的自动机 ;

② 算法自动设计 : 自动机设计的过程 , 有的很复杂 , 希望能找到一个算法 , 使用该算法实现 自动机的设计 ;

③ 语言特点 : 如果要设计能识别 某语言的自动机 , 那么需要先了解这个语言有什么特点 , 知道这个语言的特点就可以设计 识别该语言的自动机 ;

三、 正则语言运算 ★

两种正则语言之间的运算 :

前提 :

A

是一种正则语言 ,

B

是另外一种正则语言 ;

1 . 并运算 ( Union ) : 将

A, B

两个语言并在一起 , 就是将

A

语言的字符串 , 和

B

语言的字符串并在一起就可以 ;

\rm A \cup B = \{ \quad x \quad | \quad ( \; x \in A \; ) \lor ( \; x \in B \; ) \quad \}

2 . 串联运算 ( Concatenation ) : 将

A

语言的字符串 与

B

语言中的字符串串在一起 , 注意

A

语言字符串在前 ,

B

字符串在后 ;

\rm A \circ B = \{ \quad xy \quad | \quad ( \; x \in A \; ) \land ( \; x \in B \; ) \quad \}

3 . 星运算 ( Star ) :

\rm A^*= \{ \quad x_1 x_2 \cdots x_k \quad | \quad x_i \in A \quad \} \quad\quad (0 \leq i \leq k)

循环计算 :

  • 计算本质 : 计算的实质是循环 , 在现实中的计算 , 其本质也是不停的重复循环 , 进行计算 ;
  • 计算机作用 : 计算机可以代替重复的计算 ;
  • 循环运算抽象 : 星运算实质上是对循环运算的抽象表述 ;
  • 自动机计算 : 在有限自动机中 , 可以做循环计算 , 使用 星 计算 实现 循环计算 ;

星运算概念 :

A

如果是一种语言 , 将

A

中的有限个字符串 , 串在一起 , 组成的集合 , 称为

A^*

;

( 有限个字符串的 有限个 是不确定的值 , 可以是 10万 , 100亿

\cdots

)

星运算结果集合元素个数 :

A^*

集合的个数是无限的 ;

空字符串 : 这个字符串个数可以取值为

0

, 即空字符串 , 空字符串一定属于

A^*

四、语言运算示例 ★

语言计算示例 :

①

A

语言 :

A = \{ 001 , 10, , 111 \}

②

B

语言 :

B = \{ \varepsilon , 001 \}

1 . 并计算 : 将

A,B

两个语言的集合 , 取 并集 即可 , 计算如下 :

\rm A \cup B = \{ 001, 10 , 111 , \varepsilon \}

2 . 串联计算 :

A

语言中的任意字符串 , 与

B

语言中的任意字符串 , 串联在一起 ,

A

语言中有

3

个字符串 ,

B

语言中有两个字符串 , 那么串联的结果有

2 \times 3 = 6

个 , 计算过程如下 :

\rm A \circ B = \{ 001 , 10, 111 , 001001, 10001, 111001 \}

3 . 星计算 :

A

语言的星计算 , 该集合一定是一个无限的集合 , 如果

A

语言不是空集 , 那么该

A^*

集合个数是无限的 , 其可以由

K

个字符串组成 ,

K

取值

0

到无穷大 ,

[0 , +\infty )

;

\rm A^* = \{ \varepsilon , 001 , 10 , 111 , \cdots \}

五、正则语言封闭性 ★

正则语言具有封闭性 , 正则语言组成的集合 , 在并运算 , 串联运算 , 星运算 中 , 都是封闭的 ;

封闭性描述 :

A,B

都是正则语言 ,

A

可以找到一个自动机识别该语言 ,

B

也可以找到一个自动机识别该语言 , 那么一定可以找到一个自动机 分别可以识别

A \cup B

,

A \circ B

,

A^*

语言 ; (

3

个自动机分别识别

3

种语言 )

若

A, B

两个语言是正则语言 , 那么

A \cup B

,

A \circ B

,

A^*

都是正则语言 ;

A \cup B

语言证明 :

前提条件 :

① 已知自动机 与 语言 : 假设有自动机

M_1

识别语言

A

, 自动机

M_2

识别语言

B

;

② 设计的 新自动机 与 语言 : 设计新的自动机

M

识别语言

A \cup B

,

A \circ B

,

A^*

;

六、正则语言封闭性

A \cup B

证明

A \cup B

语言证明 :

① 无条件跳转 : 引入一个新的状态 , 这个新的状态 , 接受

\varepsilon

即可跳转到

M_1

和

M_2

的开始状态 ;

当自动机

M

启动后 , 进入开始状态 , 不需要进行任何计算 , 会无条件跳转到

M_1

和

M_2

的开始状态 ;

② 新自动机 : 自动机

M

所接受的语言 , 实际上就是

M_1

自动机所接受的语言

A

和

M_2

自动机所接受的语言

B

的并集 , 即

A \cup B

;

在这里插入图片描述

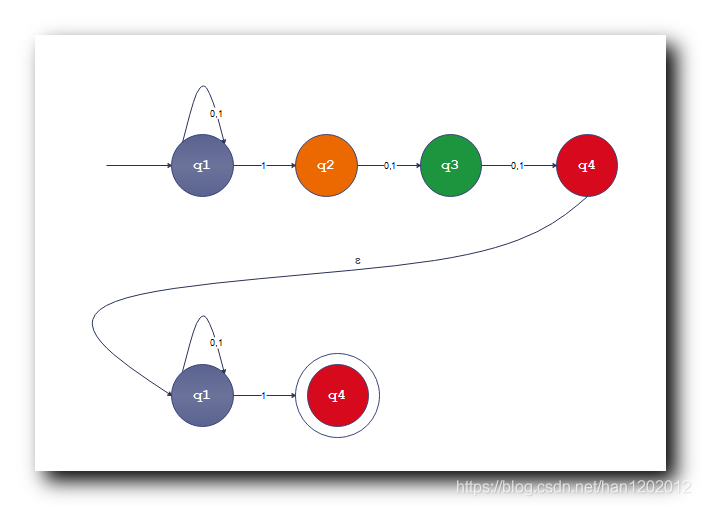
七、正则语言封闭性

A \circ B

证明

A \circ B

语言证明 :

① 旧的自动机与语言 : 假设有自动机

M_1

识别语言

A

, 自动机

M_2

识别语言

B

;

② 新的自动机与语言 : 设计新的自动机

M

识别语言

A \circ B

;

生成新自动机 : 只要引入一个

\varepsilon

箭头 , 将第一个自动机

M_1

的接受状态 , 改成非接受状态 , 使用

\varepsilon

箭头 , 指向

M_2

的开始状态即可 ;

原状态 : 上面的自动机是

M_1

, 语言

A

, 下面的自动机

M_2

, 语言

B

;

在这里插入图片描述

新状态 : 将第一个自动机

M_1

的接受状态 , 改成非接受状态 , 使用

\varepsilon

箭头 , 指向

M_2

的开始状态 ;

在这里插入图片描述

八、正则语言封闭性

A^*

证明

A^*

语言 封闭性 证明 : 一个自动机

M

识别

A

语言 , 获取识别

A^*

语言的自动机 , 只需要将 该自动机

M

的开始状态 与 接受状态 连接起来即可 ;

在这里插入图片描述

九、自动机扩展

整体思想 :

自动机是一个简单的计算模型 , 在自动机上添加

2

次简单的结构 , 就可以使该计算模型达到计算的极限 , 就是图灵机 ;

计算模型经过逐步扩张 , 达到计算的极限 ;

#集合#模型#设计#算法#字符串