本文将以具体实例形式,介绍线上判定一元函数的单调性,计算单调性区间的分界点、极值点与拐点,一元函数的极值与最值;判定多元函数的极值点、鞍点以及无条件极值、条件极值与最值的计算
- 工具:Wolfram|Alpha 计算知识引擎
- 位置:http://www.wolframalpha.com,打开网页直接操作
- 手机:可以直接打开网页操作,或者苹果店、亚马逊、Windows 应用商店下载正版App:https://products.wolframalpha.com/mobile/
特别提示:如果使用网页版执行操作,不需要下载、安装任何软件,也不需要点任何链接,直接网页打开的那个搜索文本编辑框(如下图)输入表达式就可以了!系列推文中除特别强调外,显示的结果都能直接看到的!

1、一元函数单调性判定和临界点
例1 求下列函数的单调区间与单调性的分界点
输入表达式为
where is 2x^3-9x^2+12x-3 increasing执行后的结果显示如下:

结果中不仅给出了单调增加的范围,也给出单调递减的区间,同时给出了单调性改变的临界点,也就是单调区间的分解,定义域以及图形演示.
例2 求下列函数的单调区间
输入表达式为
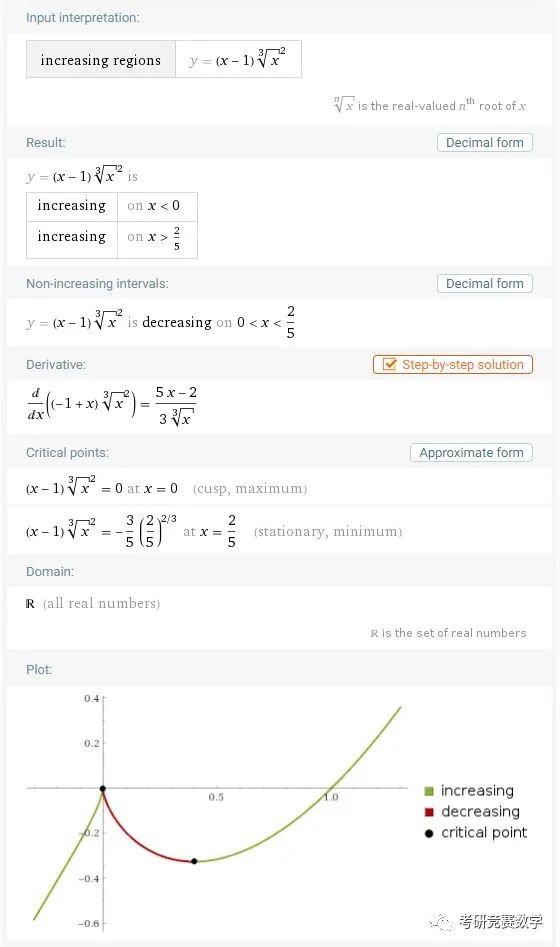
where is (x - 1) (x^(2/3)) increasing执行计算后发现只能得到大于0范围内的结果,小于0的范围不考虑,包括图形也只是显示非负的范围曲线,如下图.

也就是说当遇到一些根号里面为偶次方的函数时,执行后计算的结果只考虑大于等于0的范围,这个时候要正确完整显示,可能就需要执行一个操作。在上图结果的上方会出现一个提示,要求用the real-valued root代替操作,点击它,则完整显示计算应该得到的结果,如下图.
2、一元函数的驻点、拐点
例1 计算以下函数的驻点
输入表达式为
stationary points of x^3 (x^3 /6-x^2/5-x/4+1/3)执行后的结果显示为
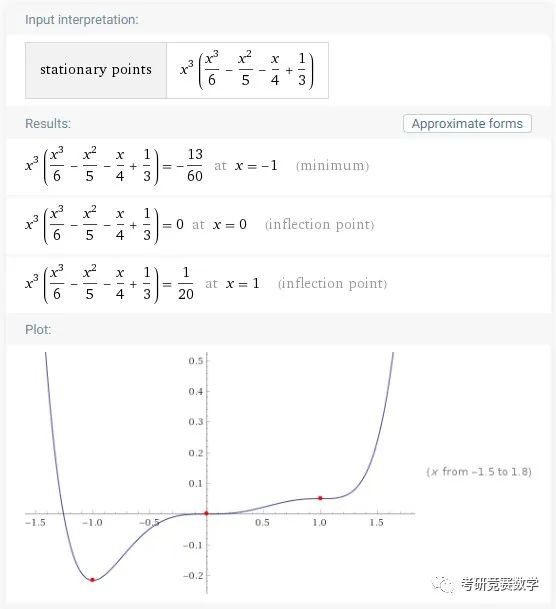
结果不仅给出稳定点的位置,而且为极值点时直接告知是极大值还是极小值,是拐点的告知为拐点.
例2 计算以下函数的拐点
输入表达式为
points of inflection of (x^2-1)^3+1执行后的结果显示为
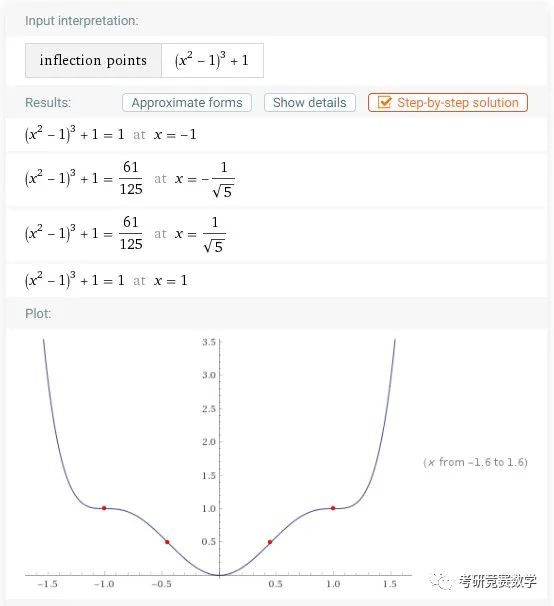
3、一元函数极值点与极值的计算
例 计算以下函数极值点和极值
输入表达式为
local extrema x^4-8x^2+2执行后的结果显示为

【注】 一般对于可导函数计算结果一般没问题,对于极值点为不可导点的位置不一定能够正确得到结果.
4、一元函数的最值计算
例1 求下列函数在指定范围内的最大值、最小值
求最大值输入表达式为
maximize |x^3-9x|,-3<=x<=5执行后的结果显示为

求最小值输入表达式为
minimize |x^3-9x|,-3<=x<=5执行后的结果显示为
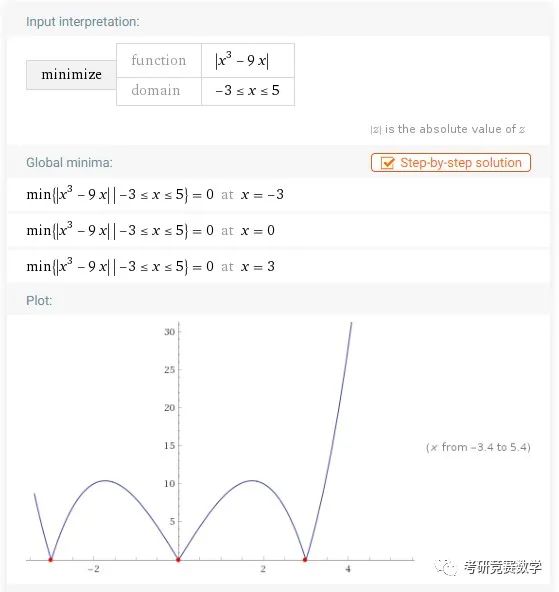
例2 求下列函数在指定范围内的最大值、最小值
求最大值输入表达式为
maximize 1/(x^2+2x+5)执行后的结果显示为

求最大值输入表达式为
minimize 1/(x^2+2x+5)结果显示该函数没有最小值. 输入
range of 1/(x^2+2x+5)计算得到值域为
5、多元函数的鞍点、极值点的判定
例 计算以下函数的驻点,并判定是否为极值点或鞍点:
输入表达式为
stationary points of x^3-y^3+3x^2+3y^2-9x执行后的结果显示为
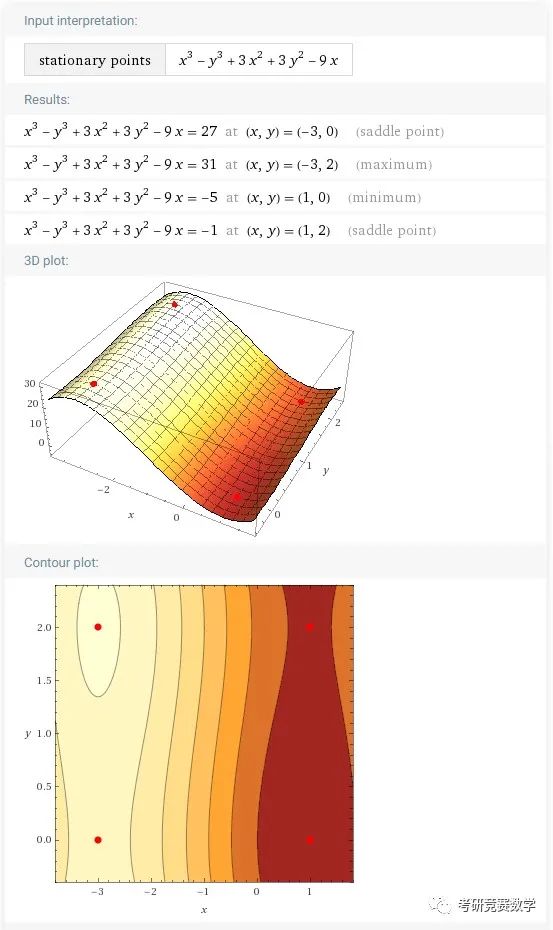
从结果可以看到 分别为极大值点和极小值点, 为鞍点
6、多元函数的无条件极值与最值
例1 计算以下函数极值点和极值
输入表达式为
local extrema x^3-y^3+3x^2+3y^2-9x执行后的结果显示为
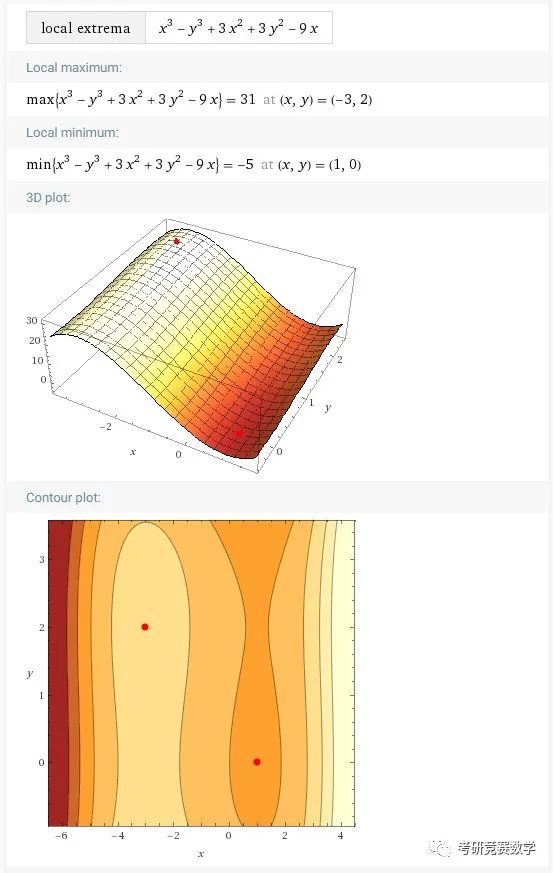
例2 求下列函数在指定范围内的最大值:
参考输入表达式为
maximize 24x siny-2x^2 siny+x^2 cosy siny, 0<x<12, 0<y<pi/2执行后的结果显示为

7、多元函数的条件极值与最值
例1 求三个正数,使它们的和为100而乘积最大. 输入表达式为
maximize x y z on x+y+z=100&&x>0&&y>0&&z>0执行后的结果显示为

例2 求下列函数在指定范围内的最大值、最小值
求最大值输入表达式为
maximize x^2+y^2-x y on |x|+|y|<=1执行后的结果显示为
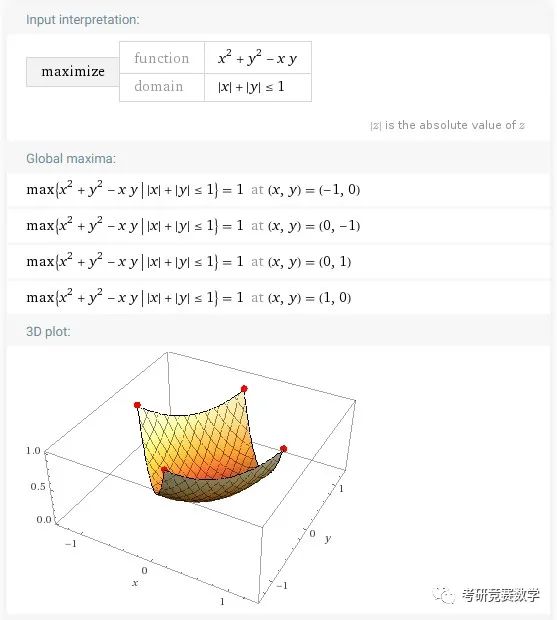
求最小值输入表达式为
minimize x^2+y^2-x y on |x|+|y|<=1执行后的结果显示为
