题目
设动物个体效应为随机遗传效应(a),日粮、性别和畜舍为固定环境效应(b),背膘厚的遗传力为0.4,请完成以下工作:
- 1,建立背膘厚的线性模型
- 2,写出模型的一般形式和矩阵形式
- 3,写出混合线性模型方程组的各组分成分
- 4,获得的估计值具有哪些特点
- 5,不同日粮和性别的效应值是多少
- 6,个体育种值是多少,是否和表型值排序一致?说明理由
处理思路
线性模型已经很清楚:
- 固定因子:日粮,性别,畜舍
- 随机因子:加性效应
- 观测值:背膘厚
矩阵形式:在R语言中构建即可
方差组分形式:因为遗传力为0.4,可以假定加性Va=2,Ve=3,则遗传力为:2/(2+3) = 0.4
问题4,问题5,问题6需要根据结果来解答
解决方案1:R语言
构建数据:
- 根据公式建立混合方程组,确定固定因子矩阵Z,随机因子矩阵X,亲缘关系逆矩阵`solve(A)``
ID <- c("A1","A2","DA","M1","C2","G","M2","CA","S","D","X")
Riliang <- c(1,1,1,1,1,1,2,2,2,2,2)
Sex <- c(2,1,2,2,1,1,2,2,1,2,1)
Sire <- c(0,0,0,0,0,"A2","A2","C2","G","A2","S")
Dam <- c(0,0,"A1","A1","A1","DA","M1",0,"M2","CA","D")
Chushe <- c(1,2,1,3,3,1,3,2,2,2,3)
mm <- c(17,20,15,30,18,12,17,16,23,19,17)
dat <- data.frame(ID,Riliang,Sex,Sire,Dam,Chushe,mm)
dat
#构建模型:ped <- dat[,c(1,4,5)]
ainv <- asreml.Ainverse(ped)$ginv
ainv_mat <- asreml.sparse2mat(ainv)
row.names(ainv_mat) = colnames(ainv_mat) <- attr(ainv,"rowNames")
round(ainv_mat,3)
dim(ainv_mat)Y = matrix(dat$mm,,1);Y
u = matrix(c(1,2,1,2,1,2,3),,1);ux = as.matrix(dat[,c(2,3,6)])/u
X = matrix(c(1,0,0,1,1,0,0,
1,0,1,0,0,1,0,
1,0,0,1,1,0,0,
1,0,0,1,0,0,1,
1,0,1,0,0,0,1,
1,0,1,0,1,0,0,
0,1,0,1,0,0,1,
0,1,0,1,0,1,0,
0,1,1,0,0,1,0,
0,1,0,1,0,1,0,
0,1,1,0,0,0,1
),11,7,byrow = T);X
Z = diag(11);ZtXX = t(X)%%X;tXX
tXZ = t(X)%%Z;tXZtZX = t(Z)%%X;tZX
tZZk = t(Z)%%Z + ainv_mat*1.5
dim(tZZk)LHS = rbind(cbind(tXX,tXZ),cbind(tZX,tZZk))
dim(LHS)tXY = t(X)%%Y
tZY = t(Z)%%Y
RHS = rbind(tXY,tZY)
dim(RHS)
library(MASS)
ab = ginv((LHS))%*%RHS
ab
R语言运行结果

解决方法2:asreml处理代码:
for(i in 1:6) dat[,i] <- as.factor(dat[,i])
moda <- asreml(mm ~ Riliang + Sex + Chushe,random = ~ ped(ID),
ginverse = list(ID = ainv) ,data=dat,start.values = T)
t <- moda$gammas.table
t$Value <- c(2,3)
t$Constraint <- "F"
modb <- asreml(mm ~ Riliang + Sex + Chushe,random = ~ ped(ID),
ginverse = list(ID = ainv) ,data=dat,
G.param = t,R.param = t)
summary(modb)$varcomp
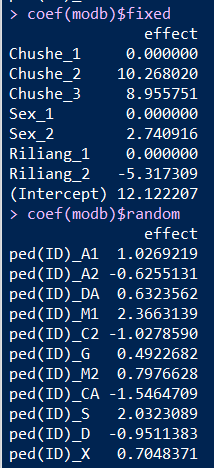
coef(modb)$fixed
dim(ab)
ab[8:18]
coef(modb)$randomasrmel运行