t 检验是比较两组均值的统计检验。这是检查两组是否来自同一群体的最常用技术之一。行业中 t 检验最普遍的应用之一是 A/B 测试,例如比较两个版本的 UI,以确定哪个版本产生更多的点击次数或在页面上花费的时间。

但是理解 t 检验方程的有点棘手,尤其是考虑到 t 检验有许多不同目标的变体。

在本文中的第一部分,我将使用简单的信号-噪声方式来解释t检验方程。
如果您查看 t 检验的上述变体,您会注意到的是每个公式都是一个分数,而分子都是两种平均值之间的某种差异。例如,单样本 t 检验计算总体均值 (mu) 与样本均值 (x) 之间的差值。独立的双样本 t 检验计算两个样本的两个均值之间的差异 - X1 和 X2。我们可以将这种差异称为信号。
t 检验方程的分母代表噪声水平。为简化起见,我们可以将其视为样本(或样本与总体)之间的方差水平。较高的值将对应更多的方差,因此会产生更多的噪音。每个分母都包含样本的标准差 (s) 和 n 的某种组合。它们一起形成了标准误差,它代表了分子(信号)的预期分布情况。
总结上面两点,信噪比代表信号强度(均值差),当噪声增大,信号减小,比值减小。如果你曾经尝试在摇滚音乐会上与某人交谈,你就会明白我的意思。但是在完全安静的情况下,即使是几乎听不见的耳语也会非常清晰。
有了这个类比,很容易看出在哪些条件下我们可以期望t检验的显著结果。一般来说,信号越高,噪声越低——p值越低(t统计量的绝对值越高)。为了说明这一点,下面我生成了两对正态分布样本,它们具有固定的均值(12和14),但样本容量和标准差不同。
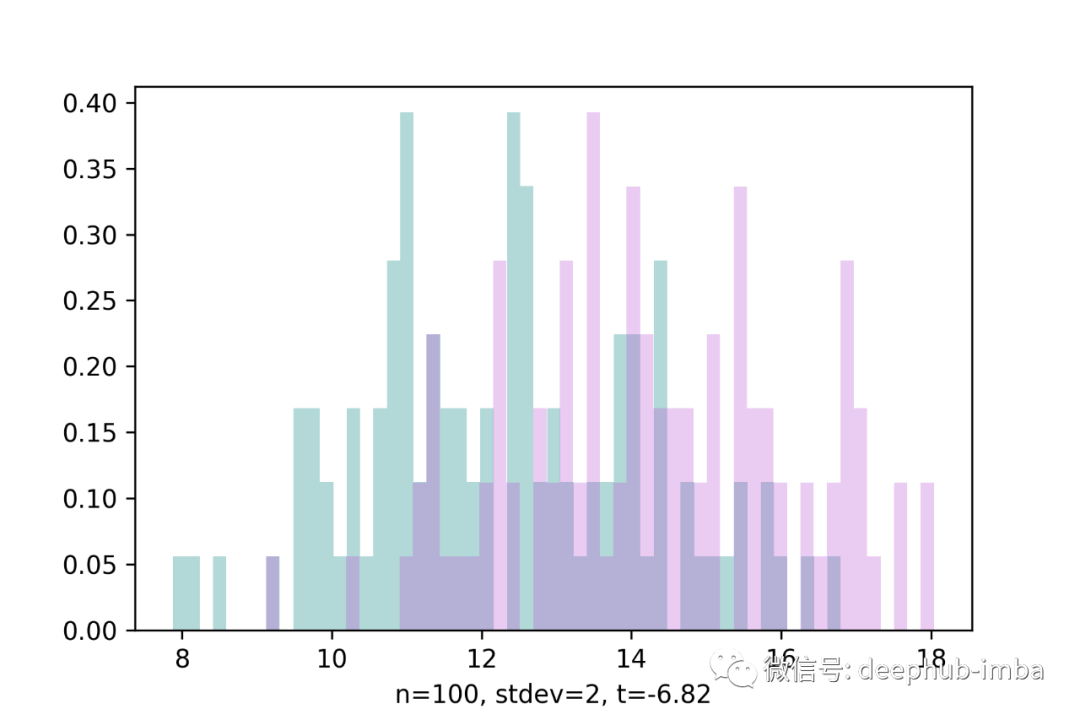
我将信号保持在-2不变,然后对第2对的噪声设置得更高,因为它取决于样本大小和标准差:较小的样本大小和较高的传播产生更高的噪声,从而削弱了信号。因此,第一对的t统计量是显著的,但第二对不显著。
下面是这种关系的一个极端例子:

样本量大,标准差小,噪声几乎为零。因此,平均值之间的任何微小差异都可以被检测到。从图形上看,这两个样本似乎没有太多重叠。由此得到的t统计量具有高度的统计显著性,这意味着两个样本来自同一总体的概率可以忽略不计。
在已经知道t值的情况下,我们可以使用统计软件或在线计算器来找到相应的p值。如果p值小于某个alpha水平(通常的选择是.01、.05和.10),那么我们可以拒绝原假设,并得出结论。也可以使用t分布表手工估计检验的p值。在这篇文章的第二部分,我们将解释如何做到这一点。
BOB想知道某一种植物的平均高度是否等于15英寸。为了验证这一点,他随机收集了20株植物的样本,发现样本均值是14英寸,样本标准差是3英寸。使用0.05 alpha水平进行t检验,以确定人口的真实平均身高是否为15英寸。
第 1 步:建立假设。
H0:μ = 15
H1:μ≠15
第 2 步:计算检验统计量。
t = (x-μ) / (s/√n) = (14–15) / (3/√20) = -1.49
步骤 3:找到检验统计量的 p 值。
要手动找到 p 值,我们需要使用具有 n-1 个自由度的 t 分布表。在我们的示例中,我们的样本大小为 n = 20,因此 n-1 = 19。
在下面的 t 分布表中,我们需要查看左侧对应于“19”的行,并尝试寻找我们的检验统计量 1.49 的绝对值。
请注意,表中没有显示 1.49,但它确实位于 1.328 和 1.729 这两个值之间。
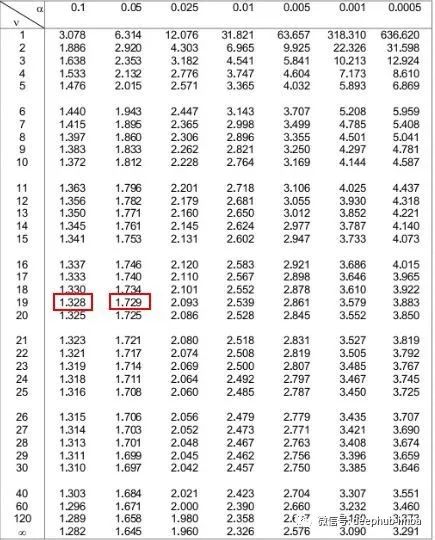
接下来,我们可以查看表格顶部与这两个数字对应的两个 alpha 级别。我们看到它们是 0.1 和 0.5。
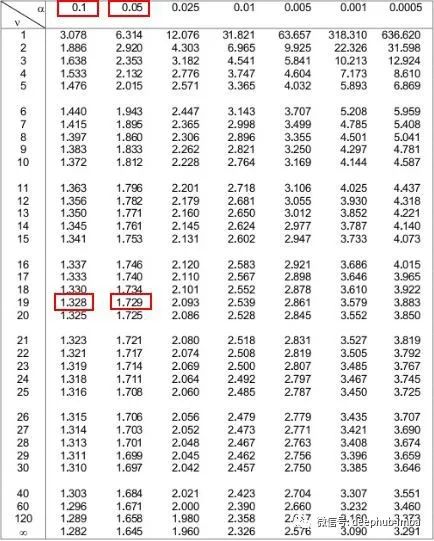
这意味着单边检验的 p 值介于 0.1 和 0.05 之间。我们称之为 0.075。由于我们的 t 检验是双边的,我们需要将此值乘以 2。因此,我们估计的 p 值为 0.075 * 2 = 0.15。
最后:得出结论
由于这个 p 值不小于我们选择的 alpha 水平 0.05,我们不能拒绝原假设。因此,我们没有足够的证据表明这种植物的真实平均高度不同于 15 英寸。
我们可以将我们的测试统计量 t 和我们的自由度插入在线 p 值计算器中,以查看我们估计的 p 值与真实 p 值的接近程度:

真实的 p 值为 0.15264,非常接近我们估计的 p 值 0.15。
在大多数情况下,可以使用 R 和 Excel 等统计软件或在线计算器来查找测试的确切 p 值,但是我们了解如何手动计算能够让我们对t检验有更好的理解。