本次介绍一个发表于Pattern Recognition的经典三维点云描述子TOLDI,首先进行算法阐述,然后再给出数据集的介绍、局部参考坐标系与描述子的评估方法。
论文地址:Jiaqi Yang, QianZhang, Yang Xiao, Zhiguo Cao, “TOLDI: An effective and robust approach for 3Dlocal shape description”, Pattern Recognition, vol. 65, pp. 175–187, 2017.
源码地址:https://github.com/TaylorAmy1995/3D-feature-description.git
1.引言
影响点云局部特征描述能力和稳定性的因素主要包括几何属性的利用以及空间信息的解码。因为点云具有无序、不规则、无拓扑结构等特性,可以凭借三维到二维投影的方式来用多张二维图像表征三维点云的几何特征,图像的表征能提供稳定的信息解码,而多视角机制可以弥补投影导致的信息损失;对于空间信息的解码,意识到充分利用三维空间信息依赖于三维物理坐标系的构建,然而敏感器的坐标系没有抗旋转的能力,因此尝试在点云局部曲面构造了一个本征、抗旋转的局部坐标系。基于上述分析,本文介绍一种基于正交投影的点云局部特征描述(TOLDI)方法(相关成果发表于Pattern Recognition 2017)。
现有的点云局部特征主要分为两类:基于和非基于局部坐标系(local referenceframe,LRF)。对于非基于 LRF 的特征,它们主要利用局部几何属性的统计量作为特征表达,例如 SI 和 FPFH。由于该类特征抛弃了空间信息,存在描述能力不足的缺陷。与之相反,基于 LRF 的特征首先在点云局部曲面建立一个本征的 LRF,然后基于 LRF 来对几何信息进行解码,例如 PS 和 RoPS。LRF 是独立于世界坐标系的局部坐标系统,一方面使得基于其解码的特征具有刚体变换不变性,另一方面为特征描述提供充分的空间信息。最近的一项评估研究表明基于 LRF 的特征在大部分公共数据库中的性能都优于非基于 LRF 的特征。
在基于 LRF 的特征中,LRF 的构建和特征表达是至关重要的两点。其原因为:1)基于 LRF 特征的有效性以及鲁棒性是建立在其依赖的 LRF 本身的稳定性基础上;2)描述子的特征表达将直接影响描述子的鉴别能力。目前典型的 LRF 方法主要分为基于协方差分析(covariance analysis,CA)和点空间分布(point spatial distributions,PSD)两类。然而,大部分基于 CA 的LRF 方法存在符号二义性的问题,基于 PSD 的 LRF 方法对噪声和点云分辨率变化较为敏感。特征表达的重点在于探索一种有效且鲁棒的方式来解码隐含在点云局部曲面的几何信息。经典示例包括二维和一维的点密度表达、法向量夹角、局部深度以及这些表达的结合。但是,目前大部分特征表达仍然存在特征描述能力不足的问题,其主要是由于从三维到二维或一维投影带来的信息损失造成的。
对于上述问题,本文介绍一种称为正交投影(triple orthogonal localdepth images, TOLDI)的方法来获得有效、鲁棒且高效的特征描述。为了建立稳定的 LRF,该描述子利用关键点周围的部分邻域点集来计算其法向量并将该向量作为 LRF 的 z 轴;LRF 的x 轴是通过所有邻域点的投影向量和来计算的;为了达到对噪声、数据分辨率变化、嘈杂以及遮挡的鲁棒性,该方法为每个投影向量赋予权重;LRF 的 y 轴则是直接通过向量叉乘所得。对于特征表达,每个邻域点到一个虚拟平面的距离,或称为局部深度,被采用来表达一个视角下的局部几何信息。这种表达的优点在于对本征几何信息的保持和高效性。为了解决由于嘈杂或遮挡造成的信息损失,选取 LRF 中的三个正交视角平面来达到一种全面的信息描述。通过将这些局部深度特征串接为一维向量,即可得到最终的 TOLDI 特征。和许多之前需要点云曲面信息的方法不同,TOLDI 可以直接在点云中进行计算而不需要三角化的过程。主要贡献如下:
• 一种可重复性高和对噪声、点云分辨率变化、嘈杂、遮挡鲁棒的 LRF。其亦可受用于现有其它基于 LRF 的特征描述子来提升它们的匹配性能;
• 一个基于正交投影的 TOLDI 点云局部特征描述子,具有良好的区分性、鲁棒性和时效性。
2.正交投影特征描述
接下来将详述正交投影 TOLDI 描述子。首先,介绍一个可重复性高和稳健的 LRF;该 LRF 是基于法向量以及邻域点投影向量和所计算得到。在该 LRF 基础之上,介绍 TOLDI 特征表达;TOLDI 是通过虚拟视角平面选择、局部邻域点投影、局部深度特征计算以及子特征串接计算所得。
局部坐标系建立
局部坐标系即在点云局部曲面中建立的本征三维坐标系(图1(a)),该坐标系独立于世界坐标系。期望局部坐标系是可重复的,即其运动不受传感器位姿变换影响而与三维模型的刚体运动是一致的。当局部坐标系存在计算误差时,将对基于其构建的点云局部特征产生显著的负面影响(图1(b))。
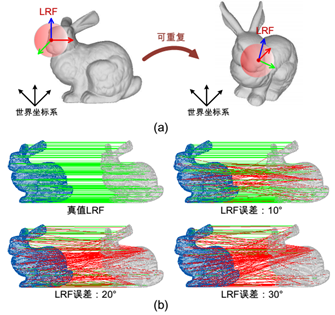
图 1 局部坐标系可重复性的定义以及局部坐标系计算误差对于三维匹配的影响。(a)中,斯坦福 bunny 模型上红色的点代指任意关键点,红色球域内的点构成了一个局部曲面,局部曲面内的三个正交轴形成了局部坐标系。如果局部坐标系的运动不受世界坐标系影响而与三维模型的刚体运动是一致的,则认为该局部坐标系是可重复的。(b)中为基于掺杂不同 LRF 角度误差的SHOT在两个 bunny 点云之间建立的匹配。LRF 误差为其对应轴之间的平均角度差。绿色线条代表正确匹配,红色线条代表错误匹配。
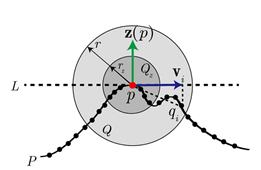
图 2 所提出的局部坐标系的二维示意图。P:点云;p:关键点;r:局部曲面支撑半径;rz:计算 z 轴的邻域半径;Q:r 对应尺度下的邻域点集;Qz:rz 对应尺度下的邻域点集;qi:Q 中任意一点;z(p):LRF 的 z 轴;L:z(p) 在关键点 p 的切平面;vi:qi 在 L 上的投影向量。
图 2 为所介绍的描述子对应的 LRF 示意图。给定点云 P 中任意关键点 p,在点 p 构建的 LRF的数学表达为:
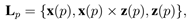
其中 x(p) 和 z(p) 为 Lp 的 x 轴和 z 轴,y 轴则可以通过向量叉乘求得。用粗体来表示向量,符号 × 来表示向量之间的叉乘。LRF 的计算因此包含两步:z 轴以及 x 轴的计算。对于 z 轴,一种直观的选择就是利用关键点的法向量。实际上,该方法的有效性已经得到了验证。因此利用一种类似的方法来计算 z轴。但是,对法向量计算所依赖的点集的选择是至关重要的。具体来说,点集中点的分布和点数将影响到最后法向量的计算。为了达到对嘈杂以及遮挡的鲁棒性,仅考虑邻域点集中的一小部分点。为了达到对点云分辨率变化的稳健性,抛弃传统的 k 近邻并采用球形邻域点。z 轴的具体计算如下:首先,以 p 为中心放置一个半径为 r 的球,球内所有的点(p 除外)被定义为点 p 的球形邻域点,这些邻域点便构成了一个局部曲面 Q = {q1, q2, . . . , qk}。然后,选取 Q 的一个子集来计算 z 轴。具体来说,Q 内所有到 p 的欧氏距离小于 rz 的点构成了一个新的点集 Qz = {q1 z, q2 z, . . . , qsz}。最后,对 Qz 进行协方差分析:
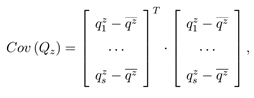
其中,s 为 Qz 中点数,qz 是 Qz 的重心。Cov (Qz)的最小特征值对应的特征向量 n(p) 被计算为 p 的法向量。由于法向量具有符号二义性,通过如下方式去除其符号二义性并计算 z 轴:
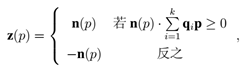
其中 k 为球形邻域点集大小,“·” 表示向量之间的点积。确定 z 轴后,下一步则是计算 x 轴。将 p 相对于 z(p) 的切平面记为 L,这一步的目的则是在 L 上找到一个具有代表性的方向。因为众多曲面会表现出平坦或对称的几何属性,对于 x 轴的计算相对于 z 轴更具挑战性。为了解决该问题,首先将所有邻域点投影在平面 L 上并为每一个邻域点 qi 计算一个投影向量:
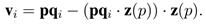
在这些投影向量的基础上,可以定义一个显著性函数来选取一个最具代表性的向量作为 x轴或者将所有这些向量融合为一个向量。侧重于后一方案因为考虑所有邻域点被证明可以得到更好的稳健性。因此,L 平面上所有向量的向量和被用来计算 x 轴:
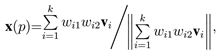
其中 |·| 代表 L2 范数。在上式中,wi1 是关联 qi 到 p 距离的一个权重:
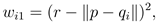
wi2是关联qi 到 L 投影距离的一个权重:
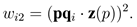
最后,LRF 的 y 轴可以由 x 轴和 z 轴之间的交叉乘积求得。值得强调的是,第一个权重 wi1 是为了提升 LRF 对嘈杂、遮挡以及不完整边缘的鲁棒性。因此,距离 p 更远的邻域点对于 LRF 的计算影响更小。第二个权重 wi2 是为了提升投影距离更大的点对于 LRF 计算的贡献,因为投影距离这个属性具有很强的可区分性并且能够在平坦区域提供高可重复性。
3.TOLDI 特征表达
在局部坐标系建立后,将基于该局部坐标系来对局部曲面的几何信息以及空间信息进行特征描述。如图3 所示,首先将 Q 变换至 LRF 的坐标系下来达到抗刚体变换的目的,旋转后的曲面记为 Q0 = {q1 0 , q2 0 , . . . , qk 0 }。接下来则需要寻找一种合适的方式进行特征表达。

图 3 TOLDI 描述子计算流程示意图。(a)中红色点代表三维模型中的一个关键点,局部曲面由关键点球体内的点集组成。

图 4 单视角下由于遮挡导致的信息损失。(a)一个二维形状。(b)单个视角下观察到的(黑色)和被隐藏的(灰色)形状信息。
在之前的研究中有许多有效的特征表达方式,例如法向量偏移角、二维投影点的密度和局部深度。这次介绍的描述子出于以下两个动机采用局部深度进行特征解码。第一,局部深度,也被称为带符号投影距离,能保留形状的主要几何信息。相比之下,其它方法的缺陷是由于三维到二维或一维投影时造成的信息损失。第二,局部深度特征计算高效。通常,局部深度特征的计算需要视点平面的选择以及三维到二维的投影。一个典型的例子就是 Snapshots 描述子,其从垂直于 LRF 中 xy 平面的一个视点来获得一张局部深度图。但是,由于嘈杂和遮挡的干扰,单个视角难以充分解码隐含在局部曲面内的有效信息,如图4 所示。因此,在 LRF 中定义多个视点平面以达到对几何信息全面表征的目的。具体来说,LRF 中三个分别距离 xy、yz 和 xz 平面为 r 且平行于这些平面的正交视角平面被用来提取局部深度图。从数学的方式来理解,这三个视点平面在 LRF 中的表达式分别为 z − r = 0、x − r = 0 和 y − r = 0。以上所有提及的操作均在 LRF 中进行,因此,这些视点平面仅仅存在于 LRF 中。如 TriSI 特征所建议,采用正交视点可以提供一种全面且相对不冗余的信息解码方式。尽管TOLDI方法所采用的视点平面选择和 TriSI 类似,但是 TOLDI 和TriSI 的区别至少在于两个方面。LRF 的建立以及特征表达是基于 LRF 的特征的关键。第一,TOLDI 依赖上述提出的基于点空间分布的 LRF 所构建,与 TriSI 所基于的协方差矩阵计算的 LRF 不同。第二,和 TriSI 所采用的自旋图表达不同,TOLDI 利用局部深度特征来形成 LDI 特征以达到更强的区分性和鲁棒性。
当视点平面选取完毕后,为 Q0 中每个邻域点相对于 xy、yz 以及 xz 平面计算局部深度特征 fixy,fiyz和 fixz:
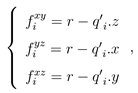
其中 q0i.x,q0i.y 和 q0i.z 分别代表 q0i 的 x 值、y 值和 z 值。这三个特征的取值范围在[0, 2r]内并被进一步归一化至 [0, 1]。随后,分别将Q0 中的点投影至这三个视点平面上并基于二维点统计的方式在每一视点平面捕获一张 w × w 大小的图像I。I 中每个像素点的值被定义为散落在该像素网格内的点集中的点所对应的最大局部深度值。像素值的选择是基于人眼感知机制的,即当人从某一视点观察物体时,被遮挡的部分是不可见的。值得注意的是在投影过程中,有些像素可能没有点散落在内,用一个取值较大的常量来表达该类像素值。最后,局部曲面由三张图像 (Ixy, Iyz, Ixz) 来进行特征表达。为了快速结合这些子特征,直接采用串接的方式来将它们合并为一个一维向量,并形成了最终的 3 × w × w 维 TOLDI 特征。
接下来,主要从理论层面分析 TOLDI 特征的三个主要特性包括刚体变换不变性、稳定性以及计算高效性:
• 刚体变换不变性:TOLDI是在一个球形邻域内计算得到并依赖于一个高可重复性的、无符号二义性的 LRF。因此,其中的几何属性(例如局部深度)是在变换至 LRF 坐标系后的局部曲面中进行计算。由于被赋予了 LRF 一样的本征属性,这些几何属性也具有刚体变换不变性,符合文献中提出的描述子不变性理论。为了结合这些不变性特征,解码不变性特征空间分布信息的 LDI“签名”(属于三维特征表达中的签名类别)被用来生成最后的特征,使得 TOLDI 最终对三维物体的刚体变换具有不变性。
• 稳定性:TOLDI的稳定性一方面依赖于 LRF 的鲁棒性,另一方面依赖于特征表达的稳定性。首先,提出的 LRF 利用邻域点集的一个子集来计算 z 轴从而减小对遮挡和嘈杂的敏感性。LRF 的 x 轴为所有邻域点集投影向量的加权向量和,其权重具有对噪声、数据分辨率变化的鲁棒性。其次,LDI 特征是由在二维投影点集进行稀疏划分得到,而且局部最大深度值被用来表征 LDI 一个维度的值。因此,噪声的存在难以明显地改变 LDI 中的维度值。同理,甚至可以忽略点密度变化的影响因为每个维度的取值只取决于一个单独的点,和点数无关。这些设计准则能明显地提升 TOLDI 在不同干扰下的稳定性。
• 计算高效性:给定一个由 k 个点组成的局部曲面,因为对于每个点仅进行 3 次相对于不同视点平面的局部深度值计算,所以TOLDI理论上的时间计算复杂度为 O(k)。除此之外,局部深度特征计算耗时低。因此,TOLDI 的计算极为高效。
4.数据集与评测方法介绍
接下来,先介绍三个标准数据集,即B3R (the Bologna 3D retrieval)、 UWAOR (the UWA 3D object recognition)以及 UWA3M(the UWA 3D modeling),如图5所示。然后再介绍评估指标。
数据集
B3R B3R 数据库是一个仿真数据库,针对的是三维形状检索应用场景。该数据库所
有的模型均来自 Stanford Repository1。原始的 B3R 数据库包含了 18 个场景和 6 个模型(模型和场景与源点云和目标点云代表的含义一致),其中场景是模型经过随机刚体变换和添加三个尺度的高斯噪声生成的。
UWAOR UWAOR 数据库是最经典的三维目标识别数据库之一。它包含了 5个模型和 50 个场景,其中每个场景由四到五个模型组成从而制造遮挡和嘈杂。这些场景数据是由 Konica Minolta Vivid 910 Scanner 传感器扫描得到。该数据集旨在测试描述子对于嘈杂和遮挡的鲁棒性。
UWA3M UWA3M 数据库针对的是点云配准场景(即 2.5D 视角数据匹配)。其分别包含来自 Chef 、Chicken、T-rex以及 Parasaurolophus模型的 22、16、16和 21个视角的点云数据。这些数据由 Konica Minolta Vivid 910 Scanner 传感器对一个模型从不同视角扫描获得。该数据集的真值变换数据由首先利用手动标注然后运行迭代最近点法(iterative closest points, ICP)获得。B3R 和 UWAOR 数据集的真值变换数据由发布者提供。该数据集的干扰包括自遮挡和孔洞。由于基于局部特征的点云匹配方法要求待匹配数据具有一定的重叠区域,然而在该数据集中,并非任意两对点云都具有重叠部分。

评估指标与方法
对于 LRF 以及描述子一般分别采用MeanCos以及精度召回率曲线(recall vs. 1-precision curve,RPC)进行定量评估。
MeanCos 指标衡量的是两个 LRF 对应轴之间的平均角度误差:
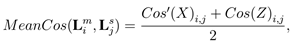
其中 Lm i 和 Ls j 分别代表模型和场景对应关键点建立的 LRF,Cos(Z) 为 Lm i 的 z 轴与经过真值矩阵变换后的 Ls i 对应的 z 轴之间夹角的余弦值,Cos(X) 为将两 LRF 的 z 轴对齐之后 x 轴之间的角度余弦值。由于 y 轴通常由 x 轴和 z 轴叉乘所得,因此不需要将该轴的误差包含进 MeanCos 指标。为了给一个数据库计算出综合指标,对于每个模型-场景点云对,随机在模型中选取 1000 个点作为关键点并利用真值变换矩阵得到这些模型关键点在场景中的对应点,然后为这些关键点计算 LRF。最后,所以模型-场景对中对应的LRF 所计算的平均 MeanCos 值被作为衡量整个数据库的综合指标。理想情况下,两个对应 LRF 之间的 MeanCos 值为1。需要强调的是,对于 MeanCos 的求取只需要计算每个关键点上的 LRF,并不需要提取局部特征。
RPC 的计算如下。给定一个模型、场景和模型到场景之间的真值变换,将每个模型点特征和所有场景点特征进行匹配并确定最近和次近的对应特征。如果最近特征距离和次近特征距离的比值小于某个阈值,这个模型点特征和场景点特征将被视为一对匹配。然后,一对匹配将被视为正确匹配如果其对应的关键点之间的空间位置误差足够小(误差阈值设为描述子支撑半径的一半)。否则,该匹配被判定为误匹配。通过改变特征比率阈值即可计算出一条曲线。其中,召回率的定义为:
召回率 = 正确匹配数量/实际对应点对数量
1-精度的定义为:
1 − 精度 =错误匹配数量/匹配数量
如果描述子同时取得了理想情况下的精度和召回率,RPC 曲线将出现在图表的左上角。
至此,本文主要阐述了一种经典的点云局部特征描述子算法TOLDI,并介绍了描述子的评估数据集、评估方法等。关于该描述子的性能与运用方法,感兴趣的读者可以阅读原论文以及github上的源程序。
本文仅做学术分享,如有侵权,请联系删文。