大家好,又见面了,我是你们的朋友全栈君
原文链接:https://www.cnblogs.com/zhangyang520/p/10969951.html
参考回答:
推荐算法:
基于人口学的推荐、基于内容的推荐、基于用户的协同过滤推荐、基于项目的协同过滤推荐、基于模型的协同过滤推荐、基于关联规则的推荐
FM:

LR:
逻辑回归本质上是线性回归,只是在特征到结果的映射中加入了一层逻辑函数g(z),即先把特征线性求和,然后使用函数g(z)作为假设函数来预测。g(z)可以将连续值映射到0 和1。g(z)为sigmoid function.

则

sigmoid function 的导数如下:

逻辑回归用来分类0/1 问题,也就是预测结果属于0 或者1 的二值分类问题。这里假设了二值满足伯努利分布,也就是

其也可以写成如下的形式:

对于训练数据集,特征数据x={x1, x2, … , xm}和对应的分类标签y={y1, y2, … , ym},假设m个样本是相互独立的,那么,极大似然函数为:
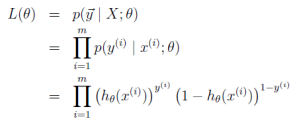
log似然为:

如何使其最大呢?与线性回归类似,我们使用梯度上升的方法(求最小使用梯度下降),那么
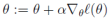
。

如果只用一个训练样例(x,y),采用随机梯度上升规则,那么随机梯度上升更新规则为:

Embedding:
Embedding在数学上表示一个maping:

,也就是一个function。其中该函数满足两个性质:1)injective (单射的):就是我们所说的单射函数,每个Y只有唯一的X对应;2)structure-preserving(结构保存):比如在X所属的空间上
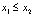
,那么映射后在Y所属空间上同理

。
那么对于word embedding,就是找到一个映射(函数)将单词(word)映射到另外一个空间(其中这个映射具有injective和structure-preserving的特点),生成在一个新的空间上的表达,该表达就是word representation。
● 协同过滤的itemCF,userCF区别适用场景
参考回答:
Item CF 和 User CF两个方法都能很好的给出推荐,并可以达到不错的效果。但是他们之间还是有不同之处的,而且适用性也有区别。下面进行一下对比
计算复杂度:
Item CF 和 User CF 是基于协同过滤推荐的两个最基本的算法,User CF 是很早以前就提出来了,Item CF 是从 Amazon 的论文和专利发表之后(2001 年左右)开始流行,大家都觉得 Item CF 从性能和复杂度上比 User CF 更优,其中的一个主要原因就是对于一个在线网站,用户的数量往往大大超过物品的数量,同时物品的数据相对稳定,因此计算物品的相似度不但计算量较小,同时也不必频繁更新。但我们往往忽略了这种情况只适应于提供商品的电子商务网站,对于新闻,博客或者微内容的推荐系统,情况往往是相反的,物品的数量是海量的,同时也是更新频繁的,所以单从复杂度的角度,这两个算法在不同的系统中各有优势,推荐引擎的设计者需要根据自己应用的特点选择更加合适的算法。
适用场景:
在非社交网络的网站中,内容内在的联系是很重要的推荐原则,它比基于相似用户的推荐原则更加有效。比如在购书网站上,当你看一本书的时候,推荐引擎会给你推荐相关的书籍,这个推荐的重要性远远超过了网站首页对该用户的综合推荐。可以看到,在这种情况下,Item CF 的推荐成为了引导用户浏览的重要手段。同时 Item CF 便于为推荐做出解释,在一个非社交网络的网站中,给某个用户推荐一本书,同时给出的解释是某某和你有相似兴趣的人也看了这本书,这很难让用户信服,因为用户可能根本不认识那个人;但如果解释说是因为这本书和你以前看的某本书相似,用户可能就觉得合理而采纳了此推荐。
相反的,在现今很流行的社交网络站点中,User CF 是一个更不错的选择,User CF 加上社会网络信息,可以增加用户对推荐解释的信服程度。
● 推荐系统的大概步骤,解决冷启动。。。
参考回答:
步骤:1)收集用户的所有信息。2)使用大数据计算平台对收集的信息进行处理,的到用户偏好数据。3)将偏好数据导入喜好类型计算算法中进行预算计算,的到预算结果。4)将推荐的结果导入数据库(redis、hbase)。5)发开一个推荐引擎,对外开放接口,输出推荐结果。
解决冷启动的方案:
1)提供非个性化的推荐
最简单的例子就是提供热门排行榜,可以给用户推荐热门排行榜,等到用户数据收集到一定的时候,再切换为个性化推荐。例如Netflix的研究也表明新用户在冷启动阶段确实是更倾向于热门排行榜的,老用户会更加需要长尾推荐
2)利用用户注册信息
用户的注册信息主要分为3种:(1)获取用户的注册信息;(2)根据用户的注册信息对用户分类;(3)给用户推荐他所属分类中用户喜欢的物品。
3)选择合适的物品启动用户的兴趣
用户在登录时对一些物品进行反馈,收集用户对这些物品的兴趣信息,然后给用户推荐那些和这些物品相似的物品。一般来说,能够用来启动用户兴趣的物品需要具有以下特点:
比较热门,如果要让用户对物品进行反馈,前提是用户得知道这是什么东西;
具有代表性和区分性,启动用户兴趣的物品不能是大众化或老少咸宜的,因为这样的物品对用户的兴趣没有区分性;
启动物品集合需要有多样性,在冷启动时,我们不知道用户的兴趣,而用户兴趣的可能性非常多,为了匹配多样的兴趣,我们需要提供具有很高覆盖率的启动物品集合,这些物品能覆盖几乎所有主流的用户兴趣
4)利用物品的内容信息
用来解决物品的冷启动问题,即如何将新加入的物品推荐给对它感兴趣的用户。物品冷启动问题在新闻网站等时效性很强的网站中非常重要,因为这些网站时时刻刻都有新物品加入,而且每个物品必须能够再第一时间展现给用户,否则经过一段时间后,物品的价值就大大降低了。
5)采用专家标注
很多系统在建立的时候,既没有用户的行为数据,也没有充足的物品内容信息来计算物品相似度。这种情况下,很多系统都利用专家进行标注。
6)利用用户在其他地方已经沉淀的数据进行冷启动
以QQ音乐举例:QQ音乐的猜你喜欢电台想要去猜测第一次使用QQ音乐的用户的口味偏好,一大优势是可以利用其它腾讯平台的数据,比如在QQ空间关注了谁,在腾讯微博关注了谁,更进一步,比如在腾讯视频刚刚看了一部动漫,那么如果QQ音乐推荐了这部动漫里的歌曲,用户会觉得很人性化。这就是利用用户在其它平台已有的数据。
再比如今日头条:它是在用户通过新浪微博等社交网站登录之后,获取用户的关注列表,并且爬取用户最近参与互动的feed(转发/评论等),对其进行语义分析,从而获取用户的偏好。
所以这种方法的前提是,引导用户通过社交网络账号登录,这样一方面可以降低注册成本提高转化率;另一方面可以获取用户的社交网络信息,解决冷启动问题。
7)利用用户的手机等兴趣偏好进行冷启动
Android手机开放的比较高,所以在安装自己的app时,就可以顺路了解下手机上还安装了什么其他的app。比如一个用户安装了美丽说、蘑菇街、辣妈帮、大姨妈等应用,就可以判定这是女性了,更进一步还可以判定是备孕还是少女。目前读取用户安装的应用这部分功能除了app应用商店之外,一些新闻类、视频类的应用也在做,对于解决冷启动问题有很好的帮助。
● 传统的机器学习算法了解吗
参考回答:
常见的机器学习算法:
1). 回归算法:回归算法是试图采用对误差的衡量来探索变量之间的关系的一类算法。回归算法是统计机器学习的利器。 常见的回归算法包括:最小二乘法(Ordinary Least Square),逻辑回归(Logistic Regression),逐步式回归(Stepwise Regression),多元自适应回归样条(Multivariate Adaptive Regression Splines)以及本地散点平滑估计(Locally Estimated Scatterplot Smoothing)。
2). 基于实例的算法:基于实例的算法常常用来对决策问题建立模型,这样的模型常常先选取一批样本数据,然后根据某些近似性把新数据与样本数据进行比较。通过这种方式来寻找最佳的匹配。因此,基于实例的算法常常也被称为“赢家通吃”学习或者“基于记忆的学习”。常见的算法包括 k-Nearest Neighbor(KNN), 学习矢量量化(Learning Vector Quantization, LVQ),以及自组织映射算法(Self-Organizing Map,SOM)。深度学习的概念源于人工神经网络的研究。含多隐层的多层感知器就是一种深度学习结构。深度学习通过组合低层特征形成更加抽象的高层表示属性类别或特征,以发现数据的分布式特征表示。
3). 决策树学习:决策树算法根据数据的属性采用树状结构建立决策模型, 决策树模型常常用来解决分类和回归问题。常见的算法包括:分类及回归树(Classification And Regression Tree,CART),ID3 (Iterative Dichotomiser 3),C4.5,Chi-squared Automatic Interaction Detection(CHAID), Decision Stump, 随机森林(Random Forest),多元自适应回归样条(MARS)以及梯度推进机(Gradient Boosting Machine,GBM)。
4). 贝叶斯方法:贝叶斯方法算法是基于贝叶斯定理的一类算法,主要用来解决分类和回归问题。常见算法包括:朴素贝叶斯算法,平均单依赖估计(Averaged One-Dependence Estimators,AODE),以及Bayesian Belief Network(BBN)。
5). 基于核的算法:基于核的算法中最著名的莫过于支持向量机(SVM)了。基于核的算法把输入数据映射到一个高阶的向量空间,在这些高阶向量空间里,有些分类或者回归问题能够更容易的解决。常见的基于核的算法包括:支持向量机(Support Vector Machine,SVM), 径向基函数(Radial Basis Function,RBF),以及线性判别分析(Linear Discriminate Analysis,LDA)等。
6). 聚类算法:聚类,就像回归一样,有时候人们描述的是一类问题,有时候描述的是一类算法。聚类算法通常按照中心点或者分层的方式对输入数据进行归并。所以的聚类算法都试图找到数据的内在结构,以便按照最大的共同点将数据进行归类。常见的聚类算法包括 k-Means算法以及期望最大化算法(Expectation Maximization,EM)。
7). 降低维度算法:像聚类算法一样,降低维度算法试图分析数据的内在结构,不过降低维度算法是以非监督学习的方式试图利用较少的信息来归纳或者解释数据。这类算法可以用于高维数据的可视化或者用来简化数据以便监督式学习使用。常见的算法包括:主成份分析(Principle Component Analysis,PCA),偏最小二乘回归(Partial Least Square Regression,PLS),Sammon映射,多维尺度(Multi-Dimensional Scaling, MDS), 投影追踪(Projection Pursuit)等。
8). 关联规则学习:关联规则学习通过寻找最能够解释数据变量之间关系的规则,来找出大量多元数据集中有用的关联规则。常见算法包括 Apriori算法和Eclat算法等。
9). 集成算法:集成算法用一些相对较弱的学习模型独立地就同样的样本进行训练,然后把结果整合起来进行整体预测。集成算法的主要难点在于究竟集成哪些独立的较弱的学习模型以及如何把学习结果整合起来。这是一类非常强大的算法,同时也非常流行。常见的算法包括:Boosting,Bootstrapped Aggregation(Bagging),AdaBoost,堆叠泛化(Stacked Generalization,Blending),梯度推进机(Gradient Boosting Machine, GBM),随机森林(Random Forest)。
10). 人工神经网络:人工神经网络算法模拟生物神经网络,是一类模式匹配算法。通常用于解决分类和回归问题。人工神经网络是机器学习的一个庞大的分支,有几百种不同的算法。(其中深度学习就是其中的一类算法,我们会单独讨论),重要的人工神经网络算法包括:感知器神经网络(Perceptron Neural Network), 反向传递(Back Propagation),Hopfield网络,自组织映射(Self-Organizing Map, SOM)。学习矢量量化(Learning Vector Quantization, LVQ)。
RF:通过对训练数据样本以及属性进行有放回的抽样(针对某一个属性随机选择样本)这里有两种,一种是每次都是有放回的采样,有些样本是重复的,组成和原始数据集样本个数一样的数据集;另外一种是不放回的抽样,抽取出大约60%的训练信息。由此生成一颗CART树,剩下的样本信息作为袋外数据,用来当作验证集计算袋外误差测试模型;把抽取出的样本信息再放回到原数据集中,再重新抽取一组训练信息,再以此训练数据集生成一颗CART树。这样依次生成多颗CART树,多颗树组成森林,并且他们的生成都是通过随机采样的训练数据生成,因此叫随机森林。RF可以用于数据的回归,也可以用于数据的分类。回归时是由多颗树的预测结果求均值;分类是由多棵树的预测结果进行投票。正式由于它的随机性,RF有极强的防止过拟合的特性。由于他是由CART组成,因此它的训练数据不需要进行归一化,因为每课的建立过程都是通过选择一个能最好的对数据样本进行选择的属性来建立分叉,因此有以上好处的同时也带来了一个缺点,那就是忽略了属性与属性之间的关系。
K-meas:基本K-Means算法的思想很简单,事先确定常数K,常数K意味着最终的聚类类别数,首先随机选定初始点为质心,并通过计算每一个样本与质心之间的相似度(这里为欧式距离),将样本点归到最相似的类中,接着,重新计算每个类的质心(即为类中心),重复这样的过程,知道质心不再改变,最终就确定了每个样本所属的类别以及每个类的质心。由于每次都要计算所有的样本与每一个质心之间的相似度,故在大规模的数据集上,K-Means算法的收敛速度比较慢。
初始化常数K,随机选取初始点为质心
重复计算一下过程,直到质心不再改变
计算样本与每个质心之间的相似度,将样本归类到最相似的类中
重新计算质心
输出最终的质心以及每个类
● 用mapreduce实现10亿级以上数据的kmeans
参考回答:
算法1.map(key,value)
输入:全局变量centers,偏移量key,样本value
输出:<key’,value>对,其中key’是最近中心的索引,value’是样本信息的字符串
从value构造样本的instance;
minDis=Double.MAX_VALUE;
Index=-1;
For i=0 to centers.length do
dis=ComputeDist(instance,centers[i]);
If dis<minDis{
minDis=dis;
index=i;
}
End For把index作为key’;
把不同维度的values构造成value’;
输出<key’,value’>对;
End
注意这里的Step 2和Step 3初始化了辅助变量minDis和index;Step 4通过计算找出了与样本最近的中心点,函数ComputeDist(instance,centers[i])返回样本和中心点centers[i]的距离;Step 8输出了用来进行下一个过程(combiner)的中间数据。
Combine函数. 每个map任务完成之后,我们用combiner去合并同一个map任务的中间结果。因为中间结果是存储在结点的本地磁盘上,所以这个过程不会耗费网络传输的代价。在combine函数中,我们把属于相同簇的values求和。为了计算每个簇的对象的平均值,我们需要记录每个map的每个簇中样本的总数。Combine函数的伪代码见算法2.
算法2.combine(key,V)
输入:key为簇的索引,V为属于该簇的样本列表
输出:<key’,value’>对,key’为簇的索引,value’是由属于同一类的所有样本总和以及样本数所组成的字符串。
初始化一个数组,用来记录同一类的所有样本的每个维度的总和,样本是V中的元素;
初始化一个计数器num为0来记录属于同一类的样本总数;
While(V.hasNext()){
从V.next()构造样本实例instance;
把instance的不同维度值相加到数组
num++;
}
把key作为key’;
构造value’:不同维度的求和结果+num;
输出<key’,value’>对;
End
Reduce函数. Reduce函数的输入数据由每个结点的combine函数获得。如combine函数所描述,输入数据包括部分样本(同一类)的求和以及对应样本数。在reduce函数中,我们可以把同一类的所有样本求和并且计算出对应的样本数。因此,我们可以得到用于下一轮迭代的新中心。Reduce函数的伪代码见算法3。
算法3.Reduce(key,V)
输入:key为簇的索引,V为来自不同结点的部分总和的样本列表
输出:<key’,value’>对,key’为簇的索引,value’是代表新的聚类中心的字符串
初始化一个数组,用来记录同一类的所有样本的每个维度的总和,样本是V中的元素;
初始化一个计数器NUM为0来记录属于同一类的样本总数;
While(V.hasNext()){
从V.next()构造样本实例instance;
把instance的不同维度值相加到数组
NUM+=num;
}
数组的每个元素除以NUM来获得新的中心坐标;
把key作为key’;
构造value’为所有中心坐标的字符串;
输出<key’,value’>对;
End
● Kmeans
参考回答:
基本K-Means算法的思想很简单,事先确定常数K,常数K意味着最终的聚类类别数,首先随机选定初始点为质心,并通过计算每一个样本与质心之间的相似度(这里为欧式距离),将样本点归到最相似的类中,接着,重新计算每个类的质心(即为类中心),重复这样的过程,知道质心不再改变,最终就确定了每个样本所属的类别以及每个类的质心。由于每次都要计算所有的样本与每一个质心之间的相似度,故在大规模的数据集上,K-Means算法的收敛速度比较慢。
初始化常数K,随机选取初始点为质心
重复计算一下过程,直到质心不再改变
计算样本与每个质心之间的相似度,将样本归类到最相似的类中
重新计算质心
输出最终的质心以及每个类
● 协同过滤中的算法怎么细分
参考回答:
协同过滤算法通过对用户历史行为数据挖掘发现用户的偏好,基于不同的偏好对用户进行群组划分并推荐相似的商品。协同过的算法分为两类分为基于用户的协同过滤算法和基于物品的协同过滤的算法。基于用户的协同过滤是基于用户对物品的偏好找到相邻邻居用户然后将邻居用户喜欢的推荐给当前的用户。基于物品的协同过滤是计算邻居时采用物品本身,基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好推荐相似的物品给他。
● FM公式
参考回答:

● FM公式
参考回答:

发布者:全栈程序员栈长,转载请注明出处:https://javaforall.cn/168381.html原文链接:https://javaforall.cn