本译文自Artem sobolev 在http://artem.sobolev.name 发表的Stochastic Computation Graphs: Continuous Case。文中版权、图像代码等数据均归作者所有。为了本土化，翻译内容略作修改。
去年我介绍了一些现代的变分推理理论。 这些方法通常与深度神经网络结合使用，形成深度生成模型（例如VAE），或者利用随机控制丰富确定性模型，从而导致更好的探索。 或者您可能对分期推算感兴趣。
所有这些情况都会将您的计算图变成一个随机的 - 先前的确定性节点现在变成随机的。 如何通过这些节点进行反向传播并不明显。 在这个系列中，我想概述可能的方法。 这一次我们将看到为什么一般方法效果不佳，看看我们可以在连续的情况下做什么。
首先，我们更正式地陈述这个问题。 考虑大致的推理目标：
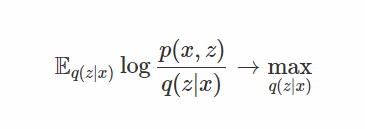
或强化学习目标：
在下面，我将使用以下符号为目标：
在这种情况下，（随机）计算图（SCG）可以用下面的形式表示[1]:
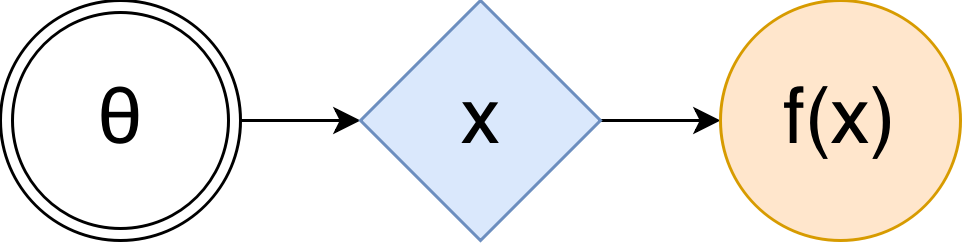
这里的 θ，双圈是一组可调参数，蓝色菱形是一个随机的节点，它随机取值，但是它们的分布依赖于θ（也许通过一些复杂而已知的函数，如神经网络），橙色圆圈是 我们正在最大化的价值。 为了使用这样的图来估计F(θ)，你只需要用你的θ，计算x的分布，从中得到尽可能多的样本，为每个样本计算f(x)，然后对它们进行平均。
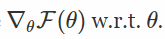
对于熟悉基本微积分的人来说，这似乎很容易：
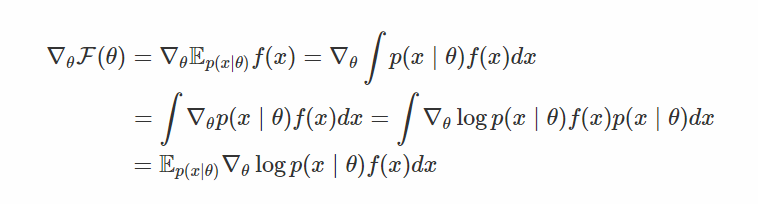
那就是这样！ 只要用这个样本x〜p（x |θ）来计算f（x），然后将结果乘以对数密度的梯度，这就是你的无偏估计 真正的渐变。 然而，在实践中，人们已经观察到，这个估计量（称为分数函数估计量，在强化学习文献[2]中也是增强的）具有很大的方差，使得高维x不切实际。
而且它有道理。 看看估算器。 它没有使用 f 的梯度信息，所以没有任何的指导来移动p（x |θ）使得期望F（θ）更高。 相反，它会尝试许多随机的xxs，对于每个样本，它都应该去使这个样本更可能的方向，并根据f（x）的大小对这些方向进行加权。 平均时，这给你真正的方向来最大限度地提高目标，但是很难用少量的样本（特别是在训练早期或者在高维空间）偶然地碰到好的x，因此变化很大。
这体现了改善这种估计量方差的两种方法的必要性，或者不同的更有效的方法。 在下面我们将考虑这两个。
重置参数法
Kingma等人完全意识到上述限制。Kingma et. al 在他们的Variational Autoencoder 论文中使用了一个聪明的技巧。 基本上，这个想法是这样的：如果一些随机变量可以被分解成其他随机变量的组合，那么我们能够转换我们的随机计算图，使得我们不需要通过随机反向传播，并且将随机性注入到模型中作为独立 噪声？
那么也就是说，对于任意的高斯随机变量x〜N（μ，σ2），我们可以将其分解为一些独立标准高斯噪声的仿射变换：其中ε〜N（0,1）（我们重新分配的分布，名称因此而来）。
然后SSG成为：
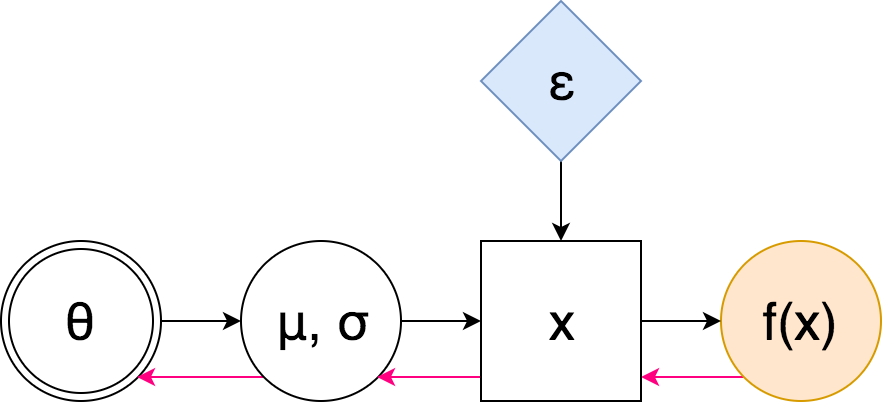
在这里，粉红色的箭头表示反向传播的“流动”：注意到我们没有遇到任何采样节点 - 因此我们不需要使用高方差分数函数估计器。 我们甚至可以有多层随机节点 - 在重新绘制之后，我们不需要通过随机样本进行区分，我们只是将它们混合在一起。让我们看看公式。
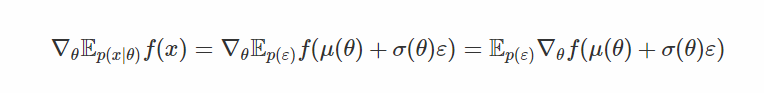
注意这次我们使用f的梯度！ 这是这个评估者与评分函数之间至关重要的区别：后来我们用他们的“分数”对随机方向进行了平均，而在这里我们学习了独立噪声的仿射变换，使得变换后的样本位于 大f（x）。 f的梯度信息告诉我们在哪里移动样本x，我们通过调整μ和σ来实现。
好吧，看起来像一个很好的方法，为什么不到处使用它？ 问题是，即使你总是可以将一个均匀分布的随机变量转换成任何其他的变量，它并不总是在计算上很容易[4].对于一些分布（Dirichlet，例如[5]），我们根本不知道任何有效的从无参数随机变换变量。
广义的重新参数化技巧
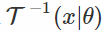
如果我们发现一个可能完全不会使x变白的变换，但是仍然会大大减少它对θ的依赖？ 这是“通用再参数化梯度”论文的核心思想。 在这种情况下，ε仍然取决于θ，但希望只是“弱”。
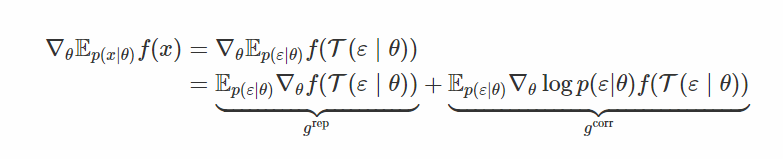
这里
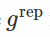
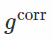
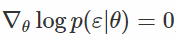
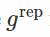
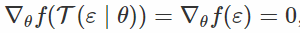
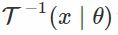
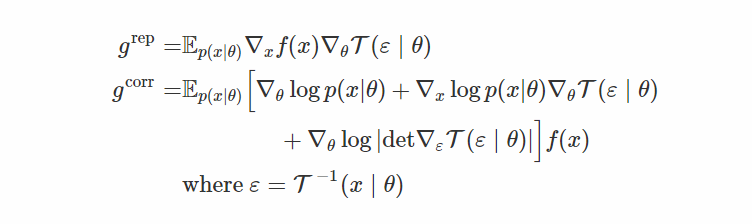
在这个公式中，我们像往常一样对x进行采样，将其通过“白化”变换
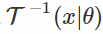
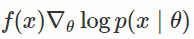
最后一个问题是选择哪个转换？ 公式作者建议使用通常的标准化变换，即用标准差减去平均值和除数。 这个选择的动机如下：a）计算方便，记得我们需要
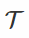
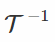
拒绝抽样视角[7]
另一个有关广义重新参数化的有趣观点来自以下思想：对于许多分布有效率的采样器，我们可以通过采样过程以某种方式反向传播吗？ 这是通过验收 - 拒绝抽样算法重新参数化梯度论文的作者决定发现的。
你想抽样一些分布p（x |θ），但是不能计算和反转它的 CDF，那么该怎么做？ 您可以使用拒收抽样程序。 基本上，您可以采取一些易于抽样的建议分布r（x |θ），找到一个比例因子
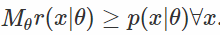
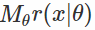
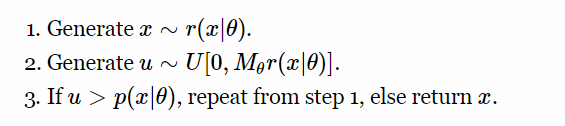
此外，在步骤1中，我们可以使用样本 ε〜r（ε）的一些变换T（ε|θ）（假设变换后的变量的密度一致性更高）。 这就是生成Gamma变量的方式：如果样本ε来自标准高斯，则通过函数x = T（ε|θ）将样本变换，然后以概率a（x |θ）接受[8]。
让我们找到导致接受相应的 x 的 εs的密度。 一些计算（补充提供）表明
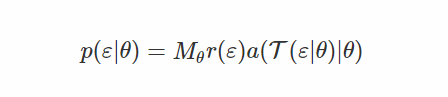
请注意，这个密度很容易计算，如果我们重新生成样本ε的参数，我们会得到样本x我们正在寻找x = T（ε|θ）。 因此，目标变成了
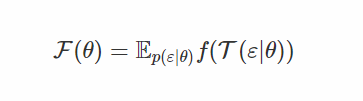
区分 w.r.t. θ 给出
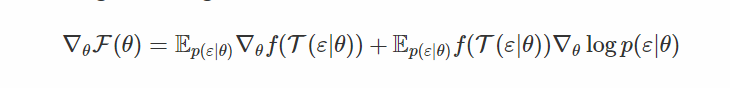
现在将这些加数与上一节中的
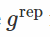
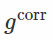
在前面的章节中，我们选择变换
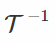
一个（非常）简单的例子
让我们来看看在一个非常简单的问题中，重新参数化的技巧实际上让我们减少了多少方差。 也就是说，我们试着最小化一个高斯随机变量[9]的预期平方（由一些正常数c移动，我们稍后会看到它是如何起作用的）：
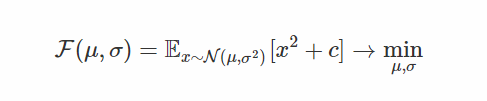
首先，重新设计的目标是
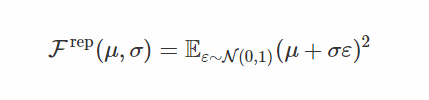
其随机梯度是
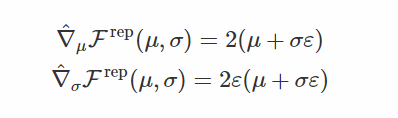
基于分数函数的梯度如下：
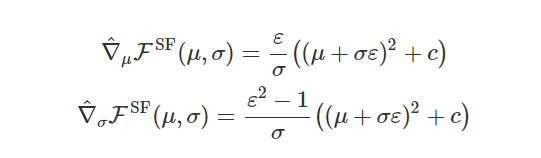
两个估计量是无偏的，但这些估计量的变化是什么？ WolframAlpha建议
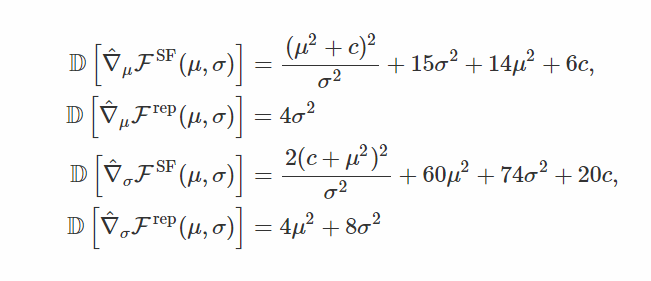
你可以看到，不仅基于分数函数的梯度总是有更高的方差，它的方差实际上随着我们逼近μ= 0，σ= 0而爆炸（除非c = 0，μ足够小以抵消σ）！ 这是因为你的方差缩小了，离平均值有点远的点会得到非常小的概率，因此基于分数函数的梯度认为它应该尽力使它们更可能。
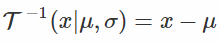
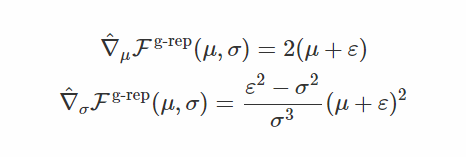
这是重新计算的梯度 w.r.t. μ 和得分函数梯度w.r.t. σ（注意在这种情况下
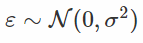
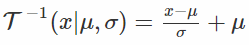
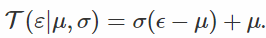
这个转换的梯度是：
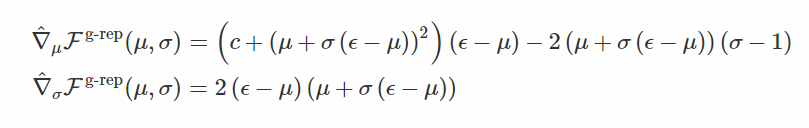
当方差σ变为零时，您已经可以看到梯度的大小不会发生爆炸。 我们来检查差异：
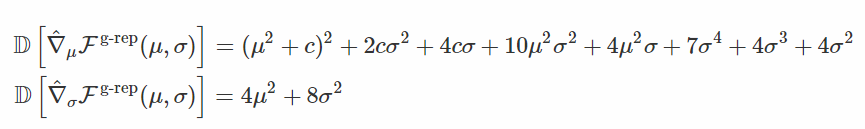
首先，我们看到梯度 w.r.t. σ 的方差与重新计算的情况的方差是一致的。 其次，我们可以证实，随着我们接近最优，方差不会爆炸。
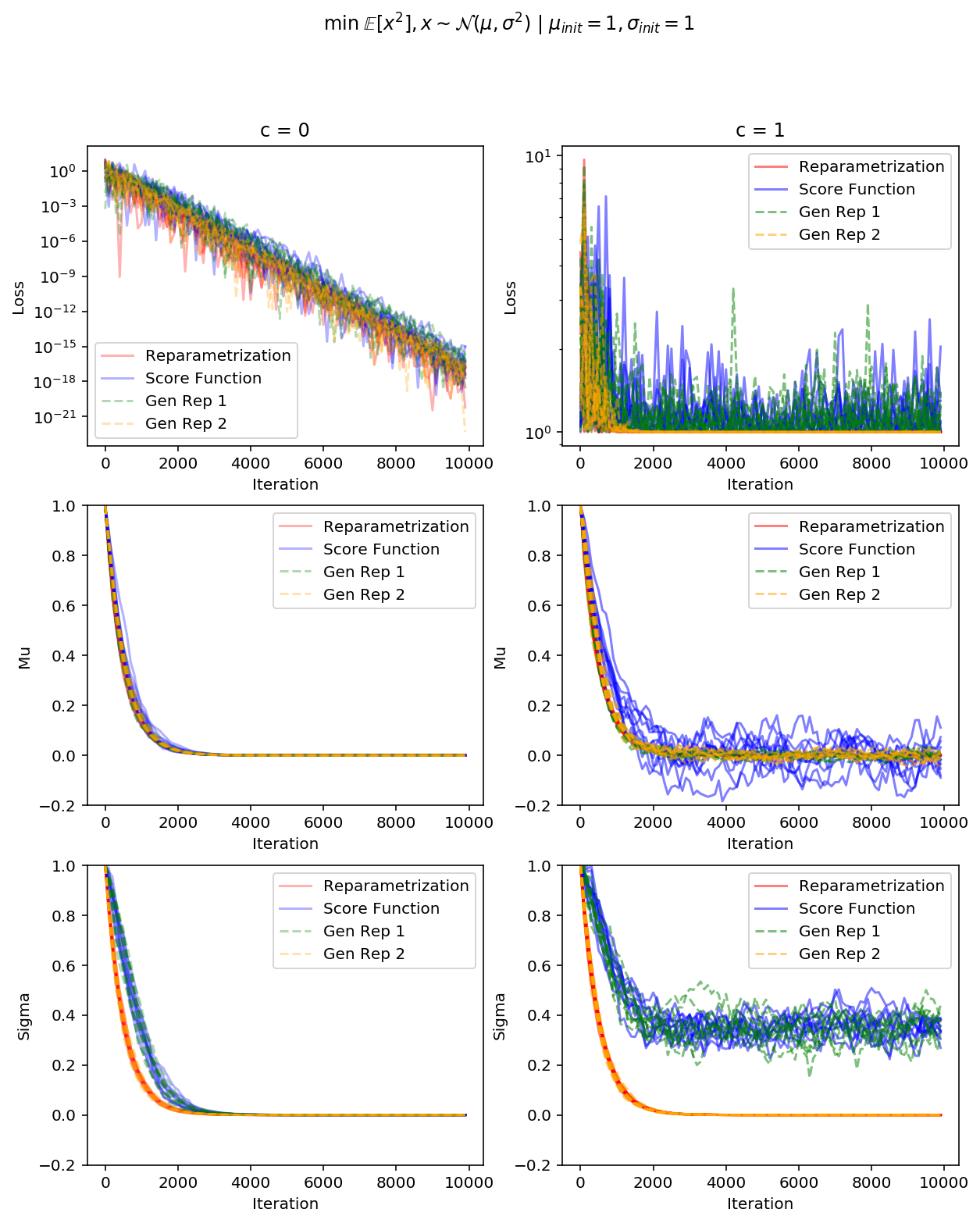
Gen Rep 1是一个广义的重新参数化，只有第一时刻变成白色，
Gen Rep 2 - 只有第二个
仿真图清楚地表明，基于分数函数的梯度和第一次广义的重新参数化不能收敛，这与我们的方差分析是一致的。 然而，第二个广义的重新参数化与完全重新参数化一样好，尽管它具有较高的方差。
我在这篇文章中编写的所有代码都可以在这里找到。 虽然这很杂乱，但我警告过你。
结论
我们已经讨论了使随机变分推理具有连续潜变量计算可行的技巧。 然而，我们常常对具有离散潜变量的模型感兴趣 - 例如，我们可能对动态选择一条或另一条计算路径的模型感兴趣，从本质上控制在给定样本上花费多少计算时间。 或者，对GAN进行文本数据训练 - 我们需要通过鉴别器的输入来反向传播。
我们将在下一篇文章中讨论这种方法。
====================================================================
- 在这篇文章中，我只会考虑只有一个随机“层”的模型，但是大致相同的数学适用于更一般的情况。↩
- 有时候人们也称这种对数导数技巧，但是，在我看来，对数导数技巧是关于导数技巧的，即，以这种方式调用估计器有点不正确。↩
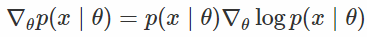[m36.png] - 这里的平等意味着双方都有相同的分配。↩
- 我们知道对于x〜p（x）用c.d.f. F（x）有F（X）〜U 0,1，因此对于标准的统一u〜U 0,1，X = F-1（u），所以总存在一个（光滑的，如果x是 连续的）从标准的均匀噪声转换到任何其他的分配。 但是，计算CDF函数通常需要昂贵的集成，这往往是不可行的。↩
- 原始的VAE论文列出了具有有效重新参数化的Dirichlet分布，然而实际上并非如此，因为您仍然需要生成参数化的Gamma变量。↩
- 从技术上讲，你可以导出密度p（ε|θ）并从中抽样 - 这样就不需要反。 但是，一般来说并不容易。↩
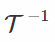[m27.png] - 本节主要基于通过拒绝抽样算法的重新参数化梯度的博客文章。↩
- 通常情况下，只是，如果我们没有一个用的r(x|θ) ，也可以用ε来表示接受概率：
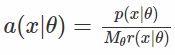[m38.png]
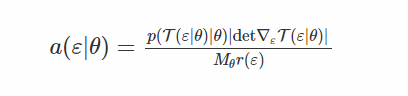
- 有人可能会认为我们的方法是有缺陷的，因为最优分布是N（0,0），这不是一个有效的分布。 然而，在我们接近这个最佳值的时候，我们只是对梯度动态感兴趣。↩
