文章目录
- 一、多项式时间规约 分析
- 二、NP 完全 ★ ( 计算理论最重要的概念 )
一、多项式时间规约 分析
多项式时间规约概念 : 【计算理论】计算复杂性 ( 多项式等价引入 | 多项式时间规约 )
下图中 , 给定 输入
, 想要知道
字符串 , 是否可以被
语言对应的算法接受 ;
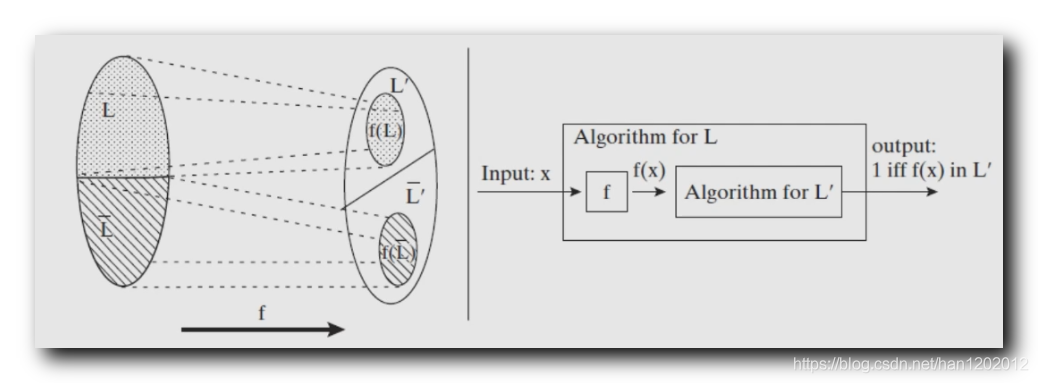
做一个规约 , 将上述问题 , 转化为
是否能被
语言对应的算法接受 ;
首先将
字符串 , 输入到函数
中计算 , 得到输出
,
然后将
输入到
算法中 , 查看该输入是否能被接受 ,
如果
接受
, 那么就说
是被
所接受的 ;
二、NP 完全 ★ ( 计算理论最重要的概念 )
NP 完全 定义 ★ :
如果 语言
是
完全的 , 必须满足如下两个条件 :
① 是
问题 : 语言
对应的计算问题必须在
中 , 换句话说就是可以找到一个多项式算法 , 可以验证该计算问题 ;
② 是
最难问题 : 在
中的任何计算问题
, 都可以在 多项式时间规约 到
, 也就是说在
中的任何计算问题 , 其难易程度都不会超过
,
是
中最难的问题 ;
中其它所有的计算问题的难以长度都不会超过
,
问题是
中最难的问题 ;
NP 完全命题 ★ : 如果
问题是
完全的 , 并且
能在 多项式时间规约 到
, 记作
, 则
也是
完全的 ;
该命题是很重要的命题 , 验证一个命题是
完全的 , 需要满足上面的两个条件 , ① 是
问题 , ② 是
最难问题 ;
将计算问题与
中最难问题
进行比较 , 是很难的 , 如果已经知道某个计算问题是
完全的 , 就不需要与
中所有问题进行比较 , 只与当前已知的
完全问题比较即可 ;
将 已知的
完全的 计算问题
, 与 要验证的
问题 , 进行规约 , 就知道
问题是否是
完全的 ;
历史已经找到了一个
完全问题 : 布尔可满足性问题 ( Boolean Satisfiability Problem;SAT ) ;