实验内容：针对给定的视频，利用图像处理基本方法实现道路路沿的检测； 提示：可利用Hough变换进行线检测，融合路沿的结构信息实现路沿边界定位（图中红色的点位置）。

处理视频文件

处理视频文件的主要流程如下：

读取视频→逐帧提取→路沿检测→逐帧保存→输出视频

用python的OpenCV实现视频文件的处理，用videoCapture打开视频文件，读取每一帧进行处理，然后用videoWriter保存成视频。

路沿检测

路沿检测的流程如下：

图像预处理→边缘检测→Hough变换

图像预处理

灰度化

从视频中取出的每一帧是彩色图像，我们可以先将它变成灰度图像，即将图像中的每个像素的RGB值（红、绿、蓝）转换为一个单一的灰度值。

image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

灰度图像只包含亮度信息，如图1所示，而不包含颜色信息。这样可以简化图像，提高处理速度，突出图像的结构，减少噪声干扰。

图1

均衡化

我们再将图像均衡化，python代码如下。

image = cv2.equalizeHist(image)

图像均衡化可以提高图像的对比度，如图2所示，突出图像的细节轮廓与边缘。

图2

二值化

将灰度图转换为只有黑白两种颜色的图像，python代码如下。

image = cv2.adaptiveThreshold(image, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 11, 2)

图像二值化可以简化图像信息，突出物体的轮廓，如图3所示。

图3

边缘检测

Canny边缘检测

Canny 边缘检测算法是John F.Canny于1986年开发出来的一个多级边缘检测算法，也被很多人认为是边缘检测的最优算法, 最优边缘检测的三个主要评价标准是:

低错误率: 标识出尽可能多的实际边缘，同时尽可能的减少噪声产生的误报。

高定位性: 标识出的边缘要与图像中的实际边缘尽可能接近。

最小响应: 图像中的边缘只能标识一次。

Canny边缘检测算法步骤如下：

高斯滤波去噪→计算梯度幅值和方向→非极大值抑制→双阈值处理

高斯滤波器去除噪声

使用高斯滤波器对图像进行平滑处理，以减少噪声的影响。

计算梯度幅值和方向

按照Sobel算子，运用一对卷积阵列 (分别作用于 x 和 y 方向):

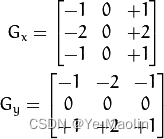
使用下列公式计算梯度幅值和方向:

梯度方向近似到四个可能角度之一(一般 0, 45, 90, 135)。

非极大值抑制

沿边缘垂直方向寻找梯度最大值，排除非边缘像素， 仅仅保留了一些细线条(候选边缘)。

双阈值处理

如果某一像素位置的幅值超过高阈值, 该像素被保留为边缘像素。

如果某一像素位置的幅值小于低阈值, 该像素被排除。

如果某一像素位置的幅值在两个阈值之间,该像素仅仅在连接到一个高于高阈值的像素时被保留。

在python中使用canny对图像进行边缘检测，高阈值为175，低阈值为75。

image = cv2.Canny(image, 75, 175)

效果如图4所示，可见canny算法可以有效的提取图像的边缘信息。

图4

但是canny检测出来的边缘中噪声比较多，我们再使用高斯滤波器模糊一下图像，在python中使用5×5的高斯滤波器模糊图像。

image = cv2.GaussianBlur(image, (5, 5), 0)

效果如图5所示，可见高斯滤波器模糊成功地去掉了一些噪声。

图5

Hough变换

Hough变换是一种用于检测图像中几何形状的技术，将图像由图像空间变换为参数空间。它最初是由保罗·霍夫（Paul Hough）在1962年提出的，用于在图像中检测直线。后来，这个方法被扩展到检测其他几何形状，如圆和椭圆。

一条直线在图像二维空间可由两个变量表示，在笛卡尔坐标系中直线可由参数斜率k和截距b表示y=kx+b，在极坐标系中可由参数极径r和极角θ表示。

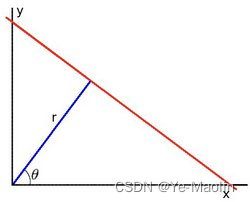
对于霍夫变换, 我们将用极坐标系来表示直线，因此直线的表达式可为：

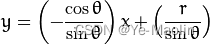
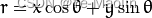
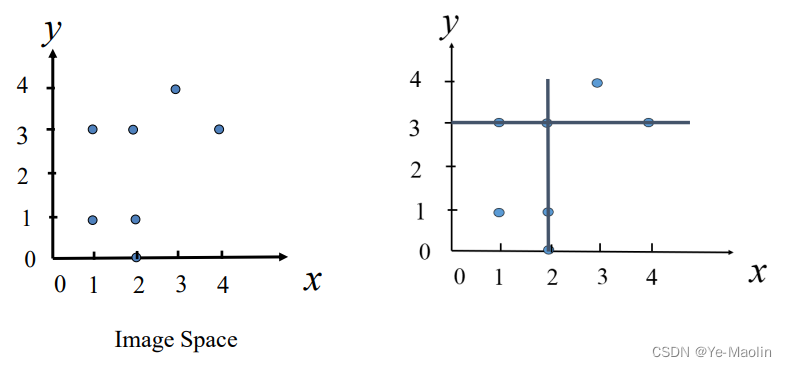
图像空间中的一条线对应Hough空间中的一个点。

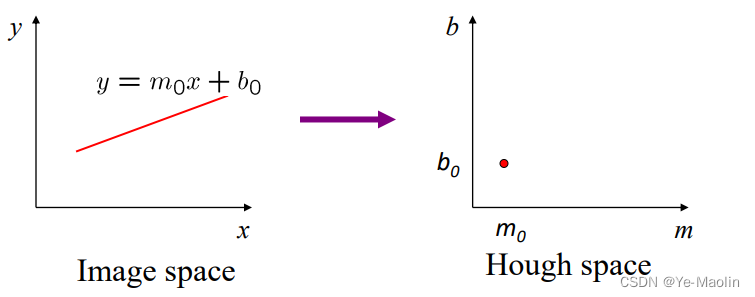
图像空间中的一个点对应Hough空间中的一条线。

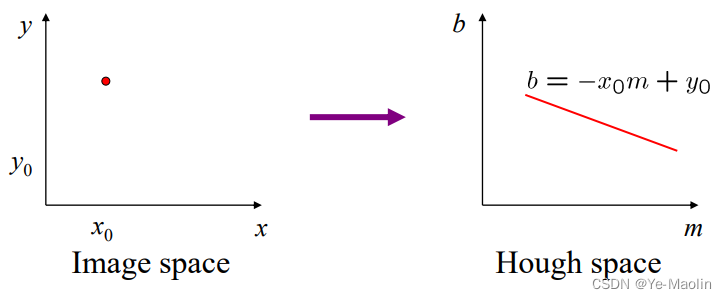
Hough变换的基本思想是将图像中的像素点映射到参数空间中，并通过在参数空间中寻找峰值来检测几何形状。对于直线检测，参数空间通常是极坐标空间，其中每个像素点在参数空间中对应一条直线。通过遍历图像中的像素点，可以累加参数空间中相应的位置，从而构建一个累加器数组。然后，在累加器数组中找到峰值，这些峰值对应于图像中存在的直线。

Hough变换步骤：

离散化θ，θ=-45,0,45,90度。

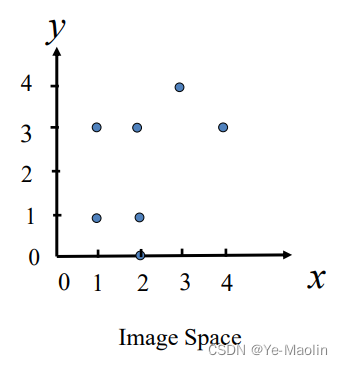
按照点的坐标（x，y）和每个角度θ求极半径r：

统计（r，θ）出现的次数

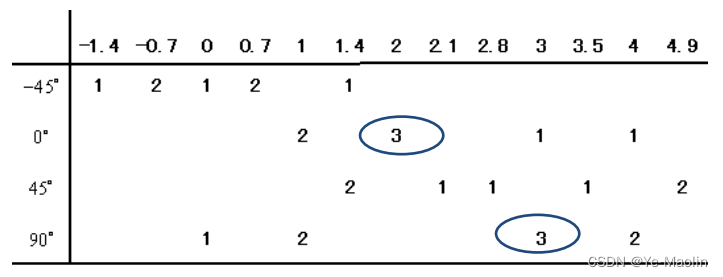
最大次数3出现在（2，0°）和（3，90°），则对应的图像空间的线为x=2和y=3。

Hough变换的优点是它对于噪声和图像变形具有一定的鲁棒性。它可以检测到不完整的、部分可见的或被噪声干扰的几何形状。因此，Hough变换在计算机视觉领域中广泛应用于图像分析、目标检测和特征提取等任务。

标准霍夫线变换

提供一组参数对 (θ, rθ) 的集合来表示检测到的直线，在OpenCV 中通过函数 HoughLines来实现。

lines = cv2.HoughLines(edge, 1, np.pi / 180, 220)

统计概率霍夫线变换

这是执行起来效率更高的霍夫线变换. 它输出检测到的直线的端点 (x0, y0, x1, y1)。在OpenCV 中它通过函数 HoughLinesP来实现。

lines = cv2.HoughLinesP(edge, 1, np.pi / 180, 100, minLineLength=50, maxLineGap=1)

Hough线变换应用路沿检测

本次我们采用标准Hough线变换来检测路沿，经过多次测试和调参，我们最后采用高斯模糊进行图像预处理，然后使用canny进行边缘提取，最后使用Hough线变换绘制直线。

def detect(image):
    gauss = cv2.GaussianBlur(image, (5, 5), 0)
    edge = cv2.Canny(gauss, 75, 175)
    # 进行Hough直线变换
    lines = cv2.HoughLines(edge, 1, np.pi / 180, 220)

视频检测效果

第一个视频是一个静止不动的路沿，检测效果如图6所示。

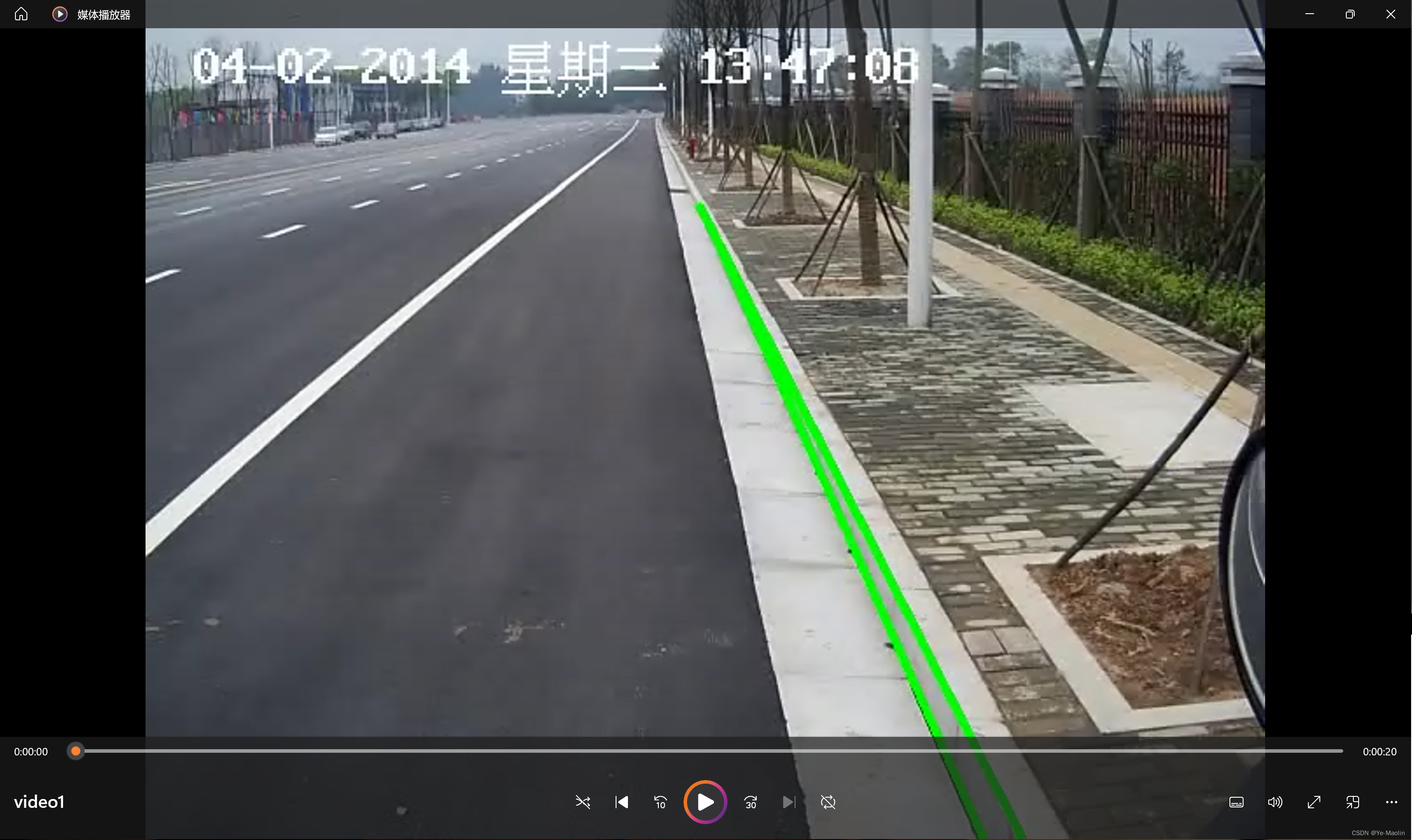
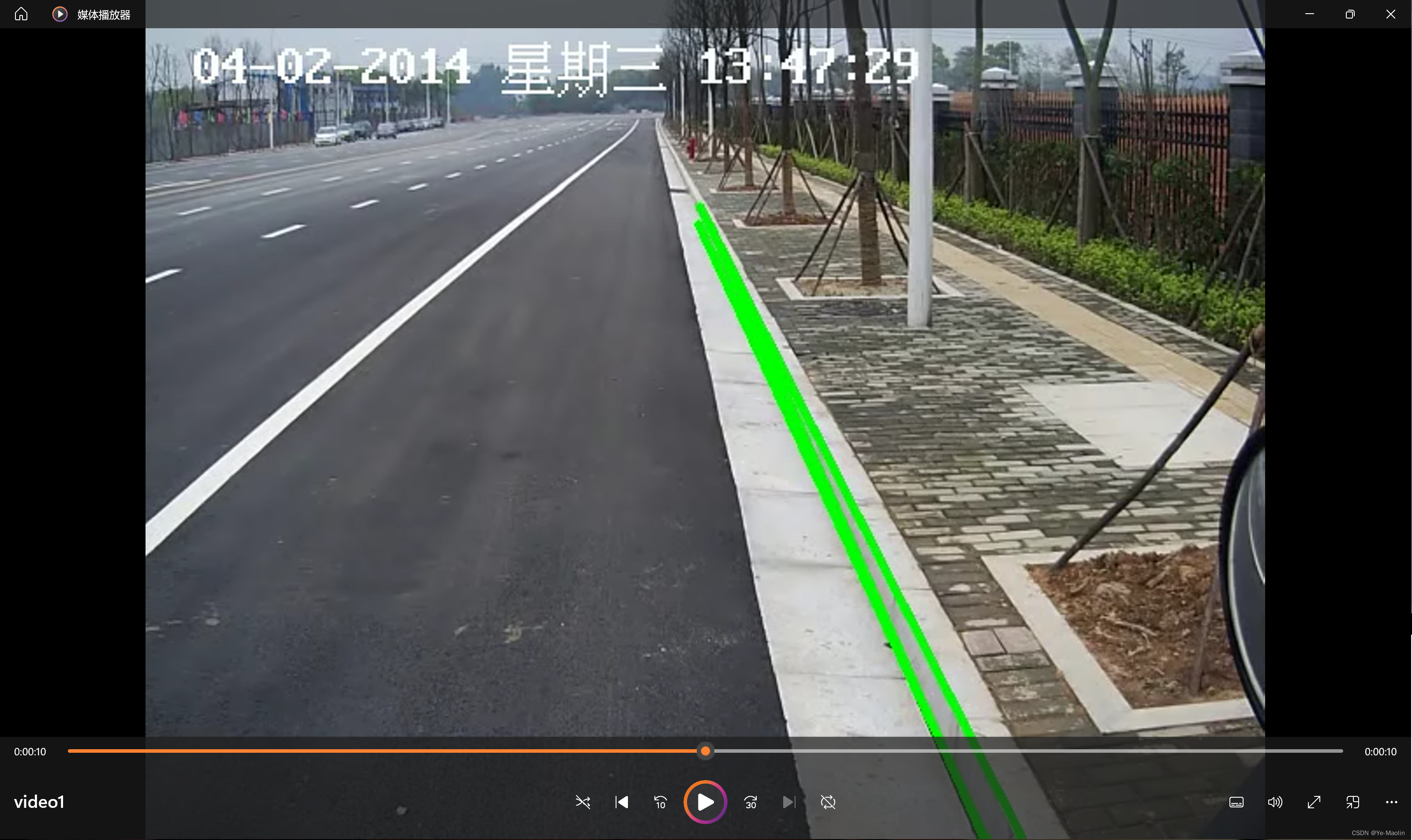
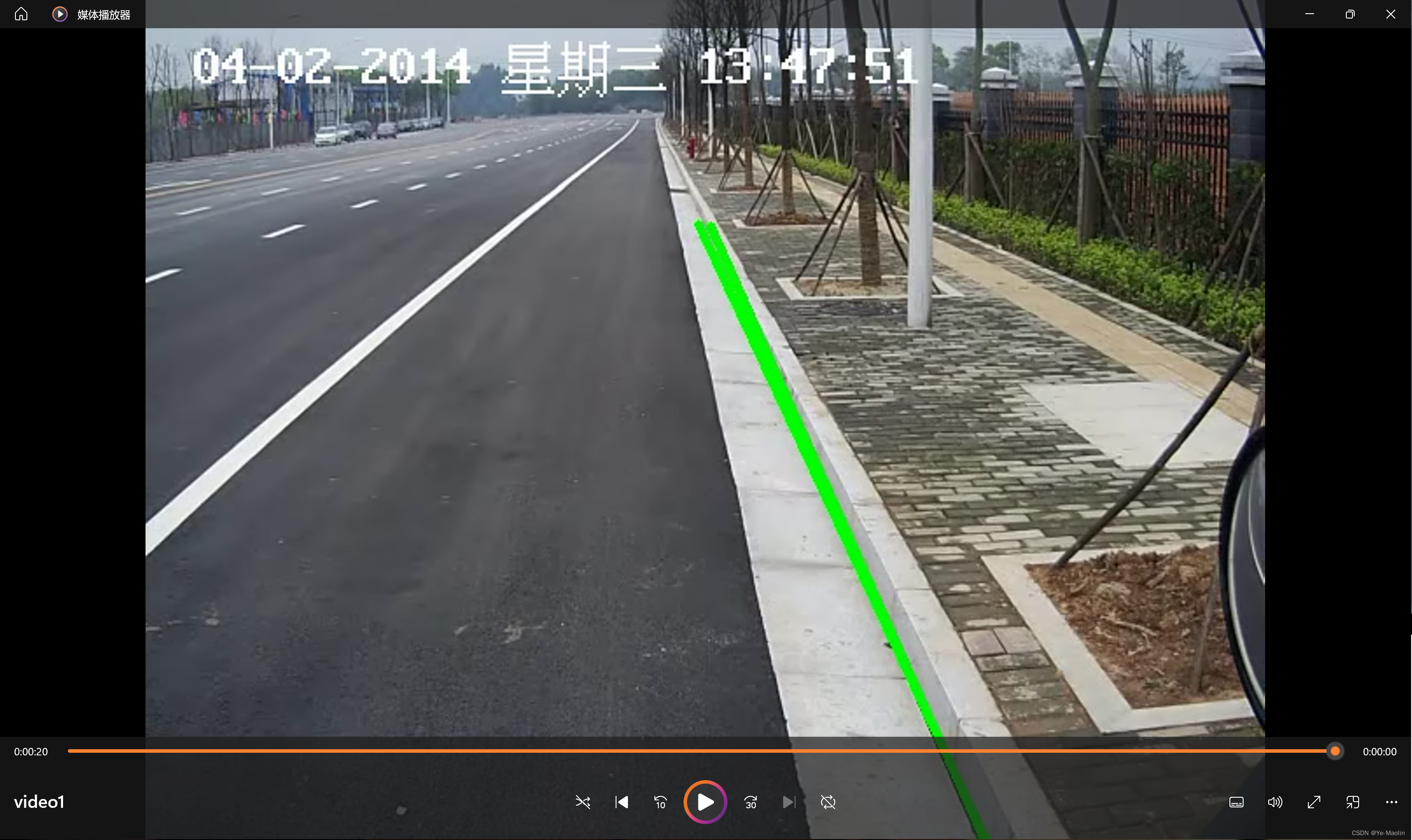
图6

第二个视频中，路沿开始变化起来，检测效果如图7所示。

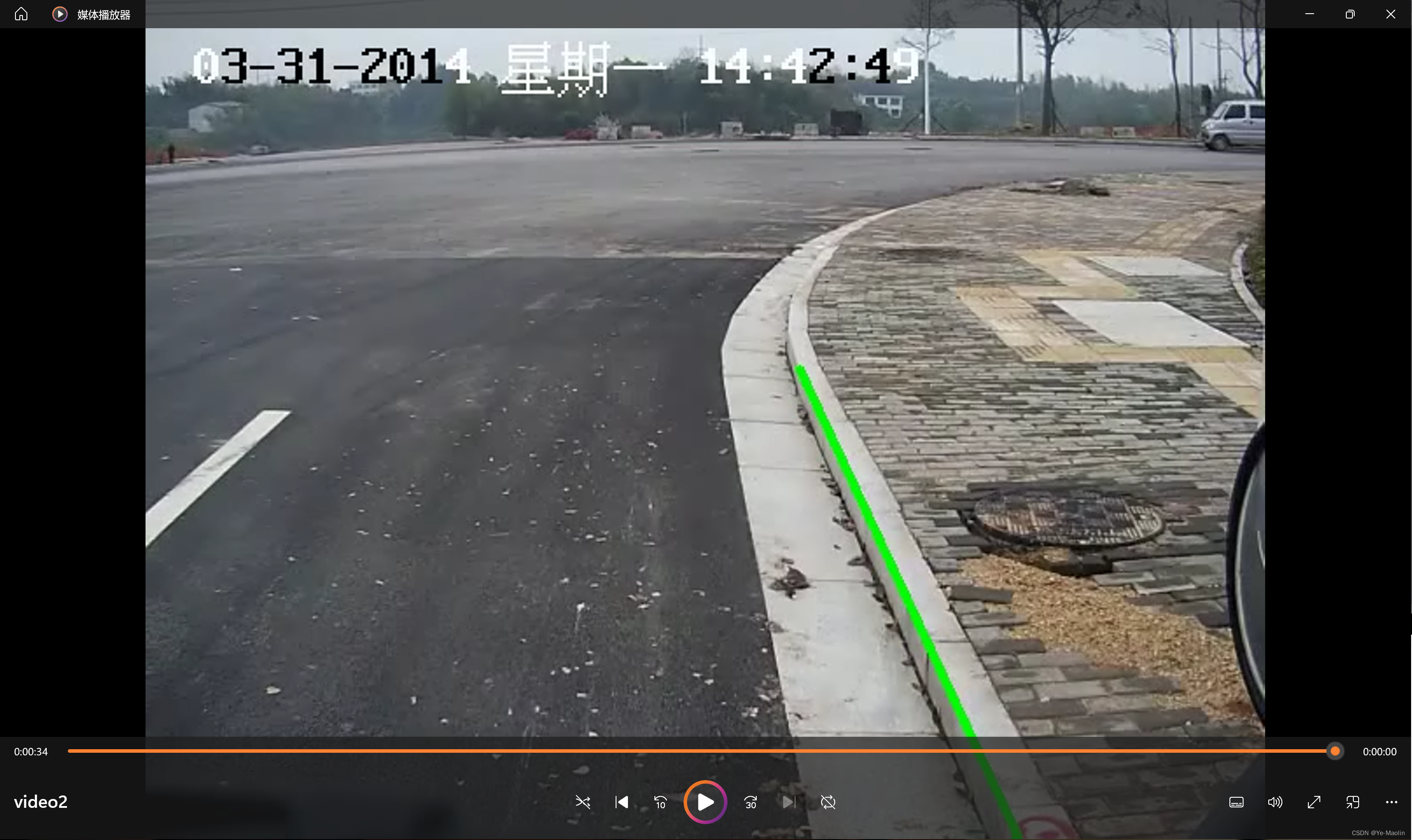
第三个视频中出现了转弯，检测效果如图8所示，因为我们只做了线变化，因此对于路沿弯曲的部分只能画出直线部分。

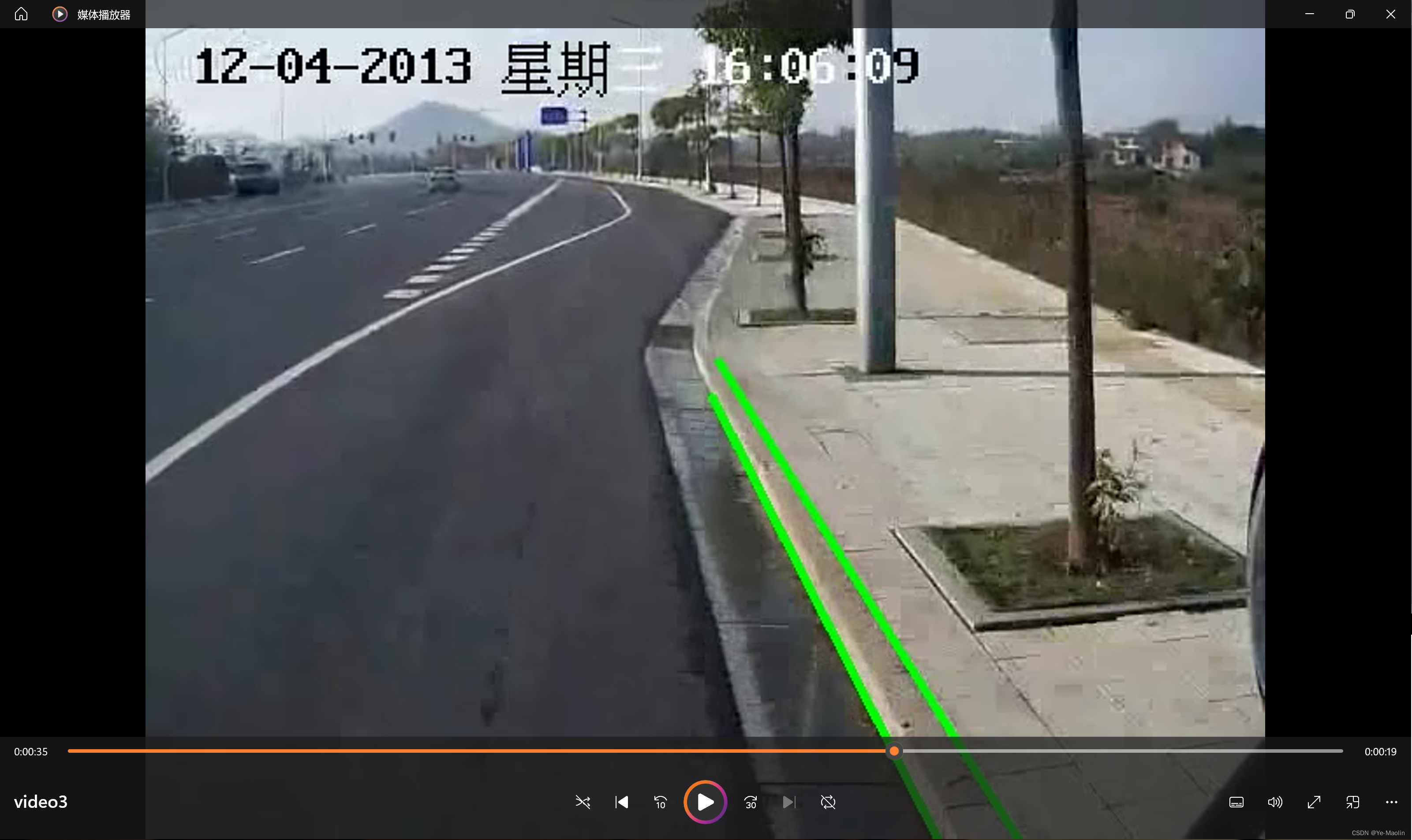
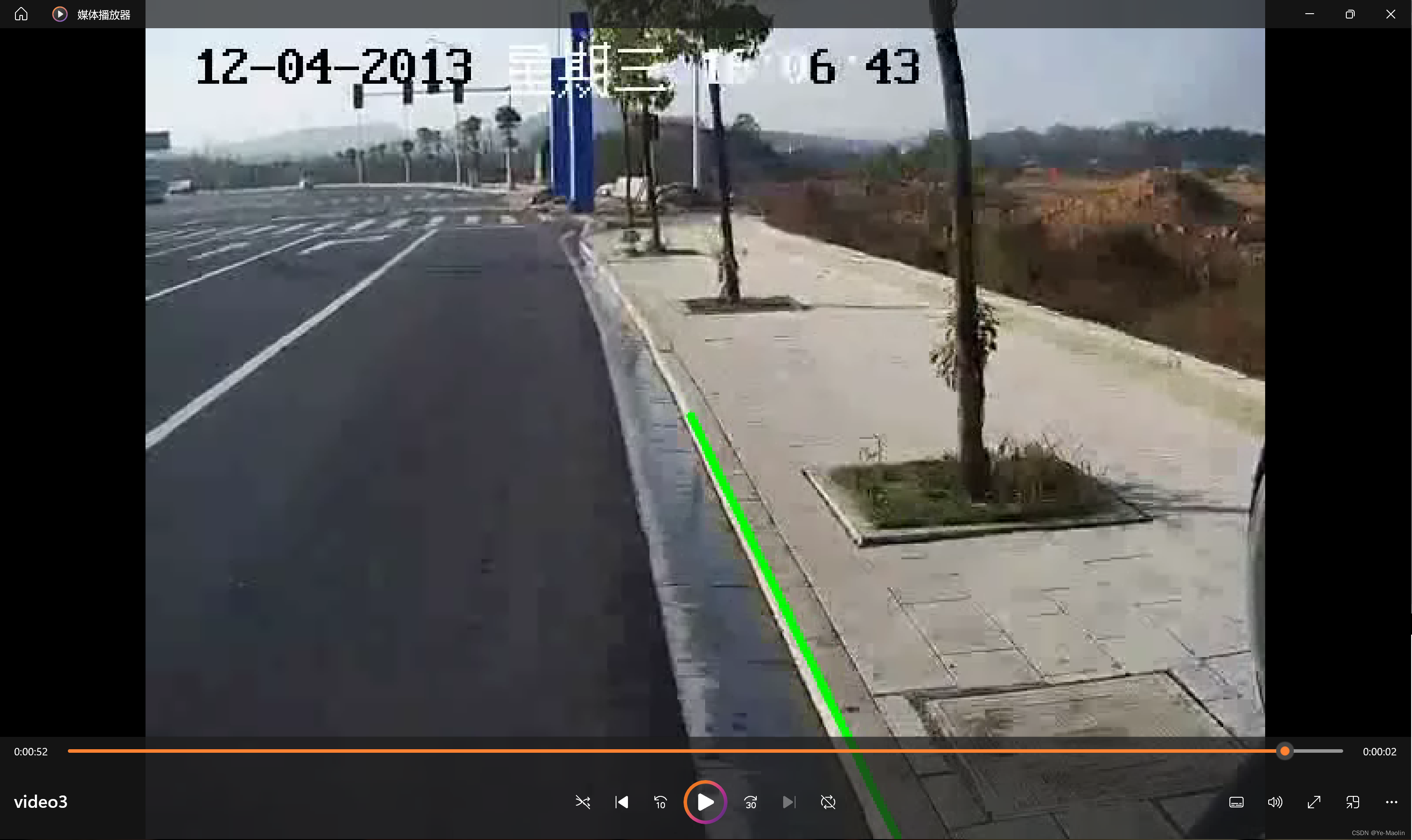
图8

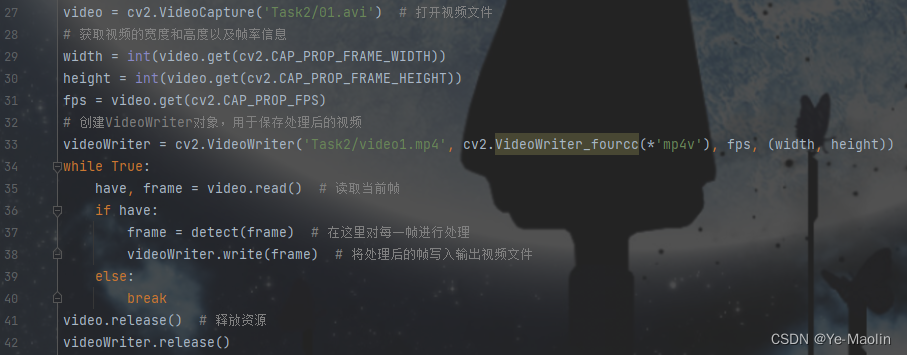
代码

import cv2

import numpy as np

def detect(image):

gauss = cv2.GaussianBlur(image, (5, 5), 0)

edge = cv2.Canny(gauss, 75, 175)

# 进行Hough直线变换

lines = cv2.HoughLines(edge, 1, np.pi / 180, 220)

# 绘制检测到的直线

if lines is not None:

for rho, theta in lines[:, 0, :]:

if theta < 2:

continue

a = np.cos(theta)

b = np.sin(theta)

x0 = a * rho

y0 = b * rho

x1 = int(x0 - 350 * (-b))

y1 = int(y0 - 350 * a)

x2 = int(x0 - 700 * (-b))

y2 = int(y0 - 700 * a)

cv2.line(image, (x1, y1), (x2, y2), (0, 255, 0), 4)

return image
video = cv2.VideoCapture('Task2/03.avi')  # 打开视频文件
获取视频的宽度和高度以及帧率信息
width = int(video.get(cv2.CAP_PROP_FRAME_WIDTH))

height = int(video.get(cv2.CAP_PROP_FRAME_HEIGHT))

fps = video.get(cv2.CAP_PROP_FPS)
创建VideoWriter对象，用于保存处理后的视频
videoWriter = cv2.VideoWriter('Task2/video3.mp4', cv2.VideoWriter_fourcc(*'mp4v'), fps, (width, height))

while True:

have, frame = video.read()  # 读取当前帧

if have:

frame = detect(frame)  # 在这里对每一帧进行处理

videoWriter.write(frame)  # 将处理后的帧写入输出视频文件

else:

break

video.release()  # 释放资源

videoWriter.release()