深层隐式生成建模的特征函数方法 (特征函数系列1)
A Characteristic Function Approach to Deep Implicit Generative Modeling 2020
https://github.com/clear-nus/OCFGAN


开创性论文:提出概率电路家族一个伟大新成员-CC

摘要
隐式生成模型(IGMs Implicit Generative Models)如 GAN 已经成为有效的数据驱动模型,用于生成样本,特别是图像。在本文中,我们将学习 IGM 的问题规划为最小化特征函数之间的期望距离。具体来说,我们最小化真实数据和生成数据分布的特征函数之间的距离,在适当选择的加权分布下。这个距离度量,我们称之为特征函数距离(CFD),可以(近似)在样本数量的线性时间复杂度内计算,与二次时间最大均值差异(MMD)相比。通过用 GAN 的评论者中的 CFD 替换差异度量,我们得到一个简单实现且稳定训练的模型。所提出的度量具有理想的理论性质,包括与生成器参数相关的连续性和可微性,以及在弱拓扑中的连续性。我们进一步提出了 CFD 的一个变体,在训练过程中还优化了加权分布参数;这消除了手动调整的需要,并相对于 CFD 导致了测试功率的提高。我们通过实验证明,我们提出的方法在各种无监督图像生成基准测试中优于 WGAN 和 MMD-GAN 的变体。
1 简介
隐式生成模型(IGMs),如生成对抗网络(GANs)[12],旨在使用来自 P 的样本学习潜在数据分布 P 的模型 Q。与规定的概率模型不同,IGMs 不需要似然函数,因此在数据似然未知或难以处理时具有吸引力。从经验上看,GANs 在许多任务中表现出色,从无监督图像生成[18]到策略学习[17]。
最初的 GAN 遭受优化不稳定性和模式崩溃的困扰,通常需要各种临时技巧来稳定训练[31]。
随后的研究揭示了 GAN 中的生成器-判别器设置最小化了真实数据和生成数据分布之间的 Jensen-Shannon 散度;这种散度具有不连续性,导致 Q 接近 P 时梯度不具信息性,从而阻碍了训练。后续的研究已经确定了一种可以简化 GAN 训练的散度的理想特性,并提出了替代的训练方案,主要使用属于积分概率度量(IPM)家族的距离[2, 34, 3]。一种流行的 IPM 是基于核的度量最大均值差异(MMD kernel-based metric Maximum Mean Discrepancy (MMD),最近的工作中有相当一部分集中在推导更好的 MMD-GAN 变体上[21, 5, 1, 22]。
在本文中,我们采用一种不同的、更基础的方法,将学习 IGM 的问题表述为最小化真实数据分布和生成数据分布的特征函数之间的期望距离。 特征函数在概率论中广泛应用,并已用于两样本检验[15, 11, 8],然而令人惊讶的是,它们尚未被用于 GAN 训练的研究。 我们发现这种方法导致了一个简单且计算效率高的损失:特征函数距离(CFD)。 计算 CFD 需要与样本数量成线性时间(不像二次时间 MMD),我们的实验结果表明,CFD 最小化导致有效的训练。
本工作为使用 CFD 训练 IGMs 提供了理论和实证支持。我们首先确定 CFD 在生成器参数方面几乎处处连续可微,并且满足弱拓扑中的连续性 - 这些关键特性使其成为适合的 GAN 指标 [3, 21]。 我们提供了补充现有 GAN 训练指标理论的新型直接证明。在算法上,我们的关键思想很简单:使用优化的加权分布下的 CFD 的经验估计来训练 GANs。 我们报告了使用合成分布和四个基准图像数据集(MNIST、CIFAR10、STL10、CelebA)进行的系统实验。
我们的实验表明,基于CFD的方法在定量评估指标上优于WGAN和MMD-GAN变种。从实际角度来看,我们发现基于CFD的GAN易于实现且训练稳定。
简而言之,这项工作的关键贡献是:
• 利用从特征函数推导出的损失训练隐式生成模型的新方法;
• 理论结果表明,所提出的损失度量在生成器参数中是连续且可微的,并满足弱拓扑中的连续性;
• 实验结果显示,我们的方法导致有效的生成模型,在各种合成和真实世界数据集上表现优于最先进的WGAN和MMD-GAN变体。
2. 概率距离和 GAN
我们首先简要回顾了生成对抗网络(GAN)框架以及用于训练GAN的最近基于距离的方法。GAN是一种生成模型,它隐式地试图学习数据分布 PX ,给定来自 PX 的样本
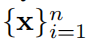
。GAN由生成器网络 gθ 和评论网络 fφ(也称为鉴别器)组成。生成器 gθ:Z → X 将从简单分布(例如,高斯分布)中采样的潜在向量 z ∈ Z 转换为数据空间中的向量 ˆx。最初的GAN [12]是通过评论家和生成器之间的对抗性两人游戏定义的;评论家试图区分真实数据样本和从生成器获得的样本,而生成器试图使其样本与真实数据无法区分。
在最近的工作中,这个两人游戏被构建为最小化真实数据分布和生成分布之间的差异。评论家 fφ 评估真实和生成样本之间的某种概率差异,并优化以最大化这种差异。在最初的GAN中,相关的(隐式)距离度量是Jensen-Shannon距离,但是后来引入了替代的差异度量,例如1-Wasserstein距离[3, 14]、Cramer距离[4]、最大均值差异(MMD)[21, 5, 1]和Sobolev IPM [28]。文献中提出的许多距离可以归结为具有不同函数类约束的积分概率度量(IPM)框架。
3. 特征函数距离
在这项工作中,我们提议使用基于特征函数(CFs)的距离度量来训练 GANs。假设 P 是与实值随机变量 X 相关联的概率测度,则 X 的特征函数
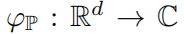
给出这个特征函数将输入的随机变量映射到复数域。

其中
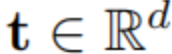
是输入参数,i = √-1。特征函数在概率论中被广泛使用,通常用作概率密度函数的替代品。随机变量的特征函数完全定义了它,即对于两个分布 P 和 Q,当且仅当 ϕP = ϕQ 时,P = Q。与密度函数不同,特征函数总是存在的,并且是一致连续且有界的:|ϕP(t)| ≤ 1。
两个分布 P 和 Q 之间的平方特征函数距离(CFD)[8, 16]定义为它们的特征函数之间的加权积分平方误差。
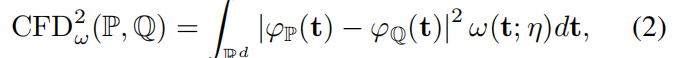


其中,
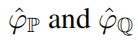
是使用 X 和 Y 计算得到的经验特征函数。
与 CFD(公式 2)相关的数量已在 [30] 和 [16] 中进行了研究,其中分析和经验稳定分布的特征函数之间的差异被最小化,以进行参数估计 discrepancy between the analytical and empirical characteristic functions of stable distributions is minimized for parameter estimation 。CFD 非常适用于这种应用,因为稳定分布不具有密度函数,这使得最大似然估计变得困难。参数拟合也已经应用于其他模型,例如高斯混合模型、稳定 ARMA 过程和仿射跳跃扩散模型 [36]。
最近,[8] 提出了基于 ECFD 的快速(O(n) 对样本数 n)两样本检验,以及 ECFD 的平滑版本,其中特征函数与解析核进行卷积。作者经验证明,ECFD 及其平滑变体相对于二次时间检验具有更好的测试效能/运行时间权衡,比 MMD 的次二次时间变体具有更好的测试效能。
3.1. 用于双样本测试的优化 ECFD
选择 ω(t; η) 的方式对于 ECFD 成功区分两个不同分布非常重要;选择适当的分布和/或参数集 η 可以更好地覆盖 P 和 Q 之间差异存在的频率。例如,如果差异集中在远离原点的频率上,而 ω(t; η) 是高斯分布,那么通过适当增大 ω(t; η) 的每个坐标的方差可以提高检验的功效。
为了增强 ECFD 的功效,我们提出优化权重分布 ω(t; η) 的参数 η(例如,与正态分布相关的方差),以最大化检验的功效。然而,在指定函数类 ω(·; η) 的丰富程度时应该谨慎——选择优化哪些参数以及相关的约束是很重要的。过度的优化可能会导致检验只关注于由于采样波动而产生的差异。作为极端例子,我们发现直接优化 t 会严重降低检验正确接受零假设 P = Q 的能力。
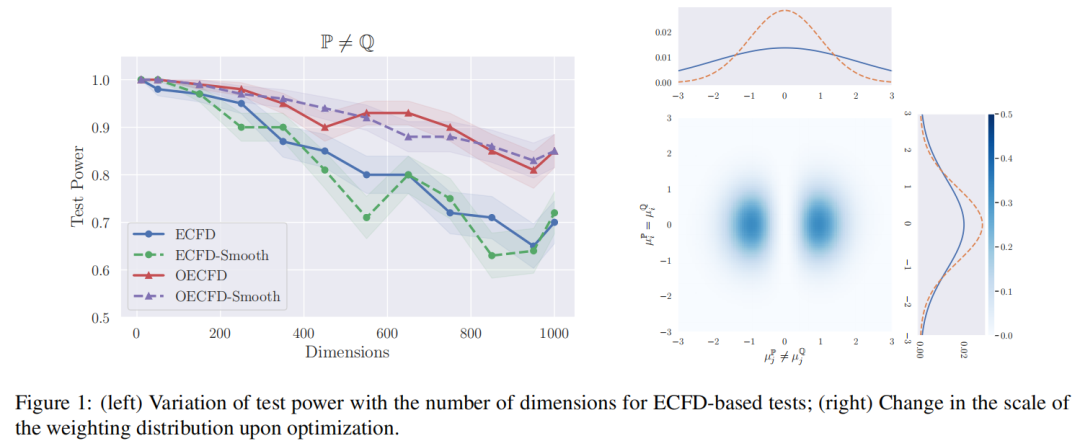
为了验证我们的方法,我们进行了一个基本实验,使用高维高斯分布,类似于 [8]。具体地,我们使用了两个多元高斯分布 P 和 Q,在所有维度中除了一个维度以外均具有相同的均值。随着维度的增加,区分来自这两个分布的样本变得越来越困难。在我们的测试中,权重分布 ω(t; η) 被选择为高斯分布 N (0, diag(σ2)),从 P 和 Q 中分别取了 10000 个样本,并将频率数量 (k) 设置为 3。我们使用 Adam 优化器对参数向量 η = {σ} 进行了 100 次迭代优化,批量大小为 1000。
图1a显示了测试功效(即零假设 P = Q 被拒绝的次数比例)随维度数量的变化情况。OEFCD 表示优化的 ECFD,而“Smooth”后缀表示[8]提出的平滑的 ECFD 变体。我们可以看到,对 η 进行优化可以增加 ECFD 和 ECFD-Smooth 的功效,特别是在更高的维度上。在优化的平滑和非平滑 ECFD 变体之间似乎没有显著差异。此外,优化改善了测试正确区分两个不同分布的能力,但并未妨碍其在分布相同时正确接受零假设的能力(请参阅附录 C)。

4. 使用 CFD 进行隐式生成建模

生成器将真实数据和生成数据之间的经验CFD最小化。我们不是最小化原始高维数据的特征函数之间的距离,而是使用一个评论者神经网络 fφ,该网络被训练为最大化在一个学习的低维空间中真实数据和生成数据分布之间的CFD。这导致了IGM的以下极小极大目标:
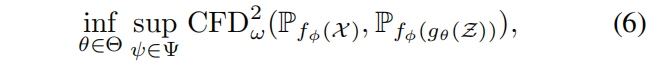
其中,ψ = {φ, η}(对应的参数空间为Ψ),η是权重分布ω的参数向量。如果我们选择不优化权重分布,则省略对η的优化。在我们的实验中,我们设置η = {σ},其中σ表示ω的每个维度的尺度。由于评估CFD需要对数据分布有所了解,在实践中,我们优化经验估计
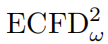
而不是
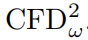
。因此,我们将这个模型称为特征函数生成对抗网络(CF-GAN)。
4.1. CFD 属性:连续性、可微分性、和弱拓扑
CFD Properties: Continuity, Differentiability, and Weak Topology
与最近提出的Wasserstein GAN和MMD GAN类似,CFD具有良好的数学性质。具体来说,CFD在生成器参数的几乎所有位置是连续且可微的(定理1)。此外,由于它在弱拓扑下是连续的(定理2),它可以为生成器gθ提供比其他缺乏这种性质的“距离”更具信息量的训练信号(例如,Jensen-Shannon散度)。接下来,我们在与[3]类似的假设下证明上述断言的证明。
以下定理正式陈述了在θ的几乎所有位置连续和可微的结果,这对于允许通过梯度下降进行训练是有益的。

证明在附录中给出。简言之,我们使用几何论证来界定特征函数之间的差异;我们将e
ia解释为圆上的一个向量,并注意到
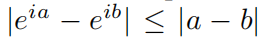
。然后,我们通过
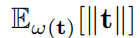
(假定为有限)和在考虑的分布下的x、x′的Lipschitz函数的平均值来对函数值的差异进行了上界限制。Lipschitz特性确保了当一个分布收敛到另一个分布时函数差异消失。
各种生成器满足局部Lipschitz假设,例如,当gθ是具有ReLU激活的前馈网络时。为确保fφ是Lipschitz的,先前工作中采用的常见方法包括权重裁剪[3]和梯度惩罚[14]。此外,许多常见分布满足
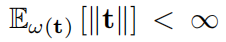
的条件,例如,高斯分布、学生t分布和具有固定σ的拉普拉斯分布。当σ是无界的并且被优化时,我们通过k σk对CFD进行了归一化,这可以防止σ趋向于无穷大。
可以在[1]的示例1中找到展示连续性结果中Lipschitz假设必要性的示例(尽管针对的是不同的度量)。在附录中,我们讨论了将定理2加强为“当且仅当”语句的条件。
4.2. 与 MMD 和之前工作的关系
CFD与最大均值差异(MMD)[13]相关联。对于来自两个分布P和Q的样本,平方MMD由以下公式给出:
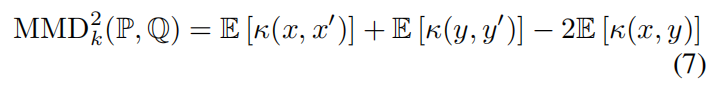

通过最小化真实样本和生成样本之间的MMD来学习生成模型是由[23]和[10]分别提出的。生成矩匹配网络(GMMN)[23]使用自动编码器将数据首先转换为潜在空间,然后训练生成网络以生成与真实潜在分布匹配的潜在向量。MMD-GAN[21]通过使用一个网络fφ进行类似的输入转换,该网络进行对抗性训练,以最大化真实分布PX和生成器分布Qθ之间的MMD;这导致了一个类似GAN的最小最大准则。最近,[5]和[1]提出了不同的理论动机的MMD-GAN评论者的正则化器,这些正则化器提高了训练效果。在我们的实验中,我们与MMD-GAN进行比较,包括具有和不具有梯度正则化的情况。
非常最近的工作[22](IKL-GAN)评估了傅立叶空间中参数化的核,然后将其用于计算MMD在MMD-GAN中。与IKL-GAN相比,我们通过特征函数而不是通过MMD推导出了CF-GAN,我们的方法不需要核评估。我们还为优化的CFD的理论属性提供了新颖的直接证明,这些证明不基于其等价于MMD。IKL-GAN利用神经网络来采样随机频率,而我们使用了一个更简单的固定分布和一个学习的尺度,减少了要调整的超参数数量。我们的方法提供了最先进的性能,这表明IKL-GAN中更复杂的设置可能不需要用于有效的GAN训练。
与此同时,通过架构和优化改进来提高GAN训练的工作也在进行中[27, 7, 18];这些研究方向与我们的工作是正交的,可以并入我们提出的模型中。
5. 实验
在本节中,我们呈现了对我们提出的模型CF-GAN的不同变体进行比较的实证结果:当参数σ与评论家一起进行优化时,我们在模型名称前面加上O,并在σ保持固定时省略它。类似地,当使用梯度惩罚[14]来强制fφ的Lipschitz性时,我们在模型名称后缀上加上GP。在没有梯度惩罚的情况下,我们将fφ的权重剪切到[-0.01, 0.01]之间。当参数σ被优化时,我们将ECFD缩放了k σk以防止σ趋向无穷大,从而确保Eω(t)[k tk] < ∞。我们将我们提出的模型与MMD-GAN的两个变体进行了比较:(i) MMD-GAN[21],它使用MMD和一组RBF核作为距离度量;(ii) MMD-GAN-GPL2[5],它基于MMD的IPM见证函数引入了一个附加的梯度惩罚,对鉴别器激活施加了一个L2惩罚,并使用了一组RQ核。我们还与WGAN[3]和WGAN-GP[14]进行了比较,因为它们与MMD-GAN[21,5]关系密切。我们的代码可以在https://github.com/crslab/OCFGAN上找到。
5.1. 综合数据
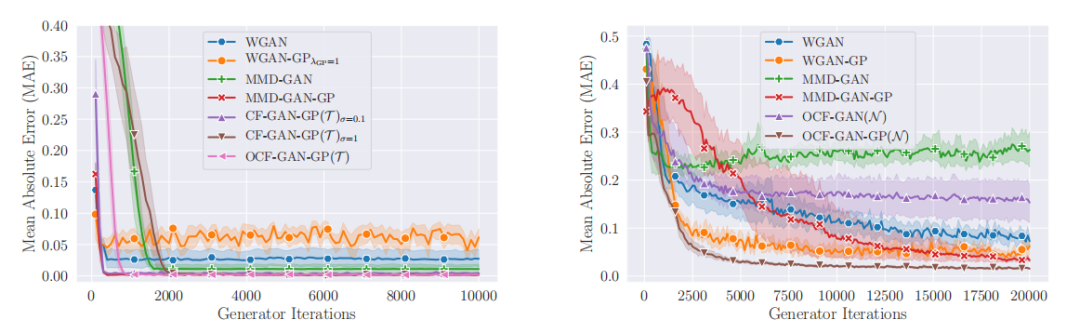
我们首先在两个合成的一维分布上测试了这些方法:一个简单的单峰分布(D1)和一个更复杂的双峰分布(D2)。这些分布是通过将z ∼ N(0, 1)使用一个函数h: R → R 进行变换构建的。对于单峰数据集,我们使用了[37]中使用的尺度平移函数形式,其中h(z) = µ+σz。对于双峰数据集,我们使用了平面流[32]中使用的函数形式,其中h(z) = αz+β tanh(γαz)。我们训练了各种GAN模型来近似变换样本的分布。训练完成后,我们将GAN学习到的变换函数ˆh与真实函数h进行了比较。我们计算了平均绝对误差(MAE) (Ez[|h(z) − ˆh(z)|])来评估模型。有关实验设置的进一步细节,请参见附录B.1。
图2a和2b显示了MAE随训练迭代次数的变化情况。对于两个数据集,具有梯度惩罚的模型收敛到更好的最小值。在D1中,MMD-GAN-GP和OCF-GAN-GP收敛到相同的MAE值,但MMD-GAN-GP的收敛速度更快。在我们的实验中,我们观察到了权重分布的尺度(初始值为1)在MAE开始减小之前迅速下降。对于尺度固定为0.1(CF-GAN-GPσ=0.1)和1(CF-GAN-GPσ=1)的实验,两个模型收敛到相同的MAE,但CF-GAN-GPσ=1的收敛速度比CF-GAN-GPσ=0.1慢得多。这表明尺度参数的优化可以加快收敛速度。对于更复杂的数据集D2,MMD-GAN-GP的收敛时间显著长于WGAN-GP和OCF-GAN-GP。OCF-GAN-GP的收敛速度最快,并且收敛到更好的最小值,其次是WGAN-GP。
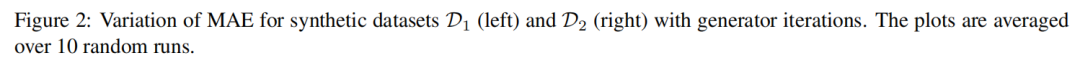
5.2. 图像生成
最近的一项大规模GAN分析[26]表明,当给定充足的计算预算时,不同的模型在性能上达到相似的最佳表现,并倡导在实际设置下比较分布。因此,我们比较了在固定的计算预算下从不同初始化得到的模型的分数。我们使用了四个数据集:1) MNIST [20]:包含60K个手写数字的灰度图像;2) CIFAR10 [19]:包含50K个RGB图像;3) CelebA [24]:包含约200K个名人面孔的RGB图像;以及4) STL10 [9]:包含100K个RGB图像。对于所有数据集,我们对图像进行中心裁剪和缩放,使其尺寸为32 × 32。
网络和超参数详情 鉴于我们的计算预算和实验设置,我们对所有模型使用了类似于[21]的DCGAN风格的生成器gθ和评论家fφ架构。对于MMD-GAN,我们使用了五个不同尺度的RBF核(5-RBF)的混合[21]。MMD-GAN-GPL2使用了混合的有理二次核(5-RQ)。核参数和梯度以及L2惩罚的权衡参数根据[5]进行设置。我们测试了两种加权分布的CF-GAN变体:高斯(N)和学生t分布(T)(自由度为2)。对于CF-GAN,我们在集合{0.2, 0.5, 1}中测试了3个尺度参数,并报告了最佳结果。用于计算ECFD的频率数量(k)设置为8。有关实现细节,请参见附录B.2。
评估指标 我们使用三个评估指标比较不同的模型:Fr´echet Inception Distance (FID) [34]、Kernel Inception Distance (KID) [5]和生成模型的Precision-Recall (PR) [33]。有关这些指标和评估过程的详细信息,请参见附录B.2。简而言之,FID计算两个多变量高斯分布之间的Fr´echet距离,而KID计算真实数据分布和生成数据分布之间的MMD(使用3次多项式核)。FID和KID都给出了单一值的分数,而PR给出了一个二维分数,将生成样本的质量与数据分布的覆盖程度区分开来。PR由一对F8(召回率)和F1/8(精确率)定义,分别代表覆盖率和样本质量[33]。
结果 接下来,我们总结了我们的主要发现,并将详细信息归入附录。表1显示了不同模型在CIFAR10、STL10和CelebA数据集上达到的FID和KID值。简而言之,我们的模型在性能上显著优于WGAN和MMD-GAN的两个变体。仅使用一个加权函数的OCF-GAN的性能优于使用5种不同核的两个MMD-GAN。

我们观察到,优化尺度参数提高了两种加权分布的模型性能,而引入梯度惩罚作为确保fφ的Lipschitz性的手段,则显著提高了所有模型的得分值。这与[14]和[5]的结果一致。总的来说,在CF-GAN变体中,具有高斯加权的OCF-GAN-GP在所有数据集上表现最好。
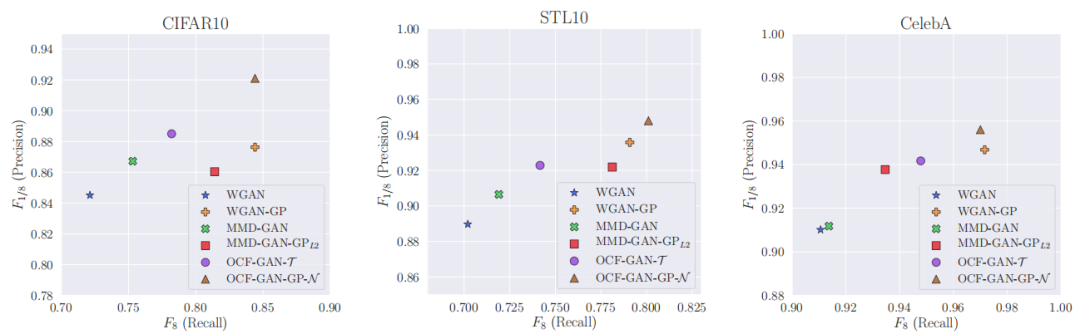
二维精确率-召回率图中的数据(见图3)进一步揭示了不同模型性能的情况。在所有数据集上,与权重剪辑(OCF-GAN)相比,添加梯度惩罚(OCF-GAN-GP)导致召回率的提高明显高于精确率。这个结果支持了最近的论点,即权重剪辑强迫生成器学习更简单的函数,而梯度惩罚更加灵活。引入梯度惩罚后,召回率的提高在CIFAR10和STL10数据集中比CelebA数据集更加显著。这个结果是直观的;CelebA数据集相对于CIFAR10/STL10来说更加统一和简单,后者包含更多种类的图像,因此可能具有更复杂且距离更远的模式。MNIST数据集上的结果显示在附录C中,所有模型均获得了良好的得分值,附录还包括使用ECFD的平滑版本和优化的平滑版本的进一步实验(在图像数据集上没有改进超过未平滑版本)。

定性结果 除了上述定量指标之外,我们还对生成的样本进行了定性分析。图4展示了OCF-GAN-GP生成的不同数据集的图像样本。我们还使用深度ResNet模型在128×128缩放版本的CelebA数据集上测试了我们的方法。由该模型生成的样本(图5)显示OCF-GAN-GP可以扩展到更大的图像和网络,并且能够生成与使用类似大小的网络的最先进方法相媲美的视觉吸引人的图像。附录C中可以找到更多的定性比较。



权重分布的影响选择权重分布并没有导致模型性能的剧烈变化。当使用权重剪辑时,T分布的表现最佳,而当使用梯度惩罚时,N分布的表现最佳。这表明适当的分布选择取决于数据集和使用的Lipschitz正则化,但整体框架对合理选择是稳健的。
我们还进行了初步实验,使用均匀(U)分布权重方案。即使均匀分布的条件
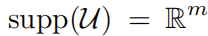
不成立,我们发现这并不会对性能造成不利影响(见附录C)。均匀权重分布对应于MMD中的sinc-kernel,这被认为是一个非特征核。我们的结果表明,当在MMD-GAN中使用时,这种核可能仍然是有效的,但我们没有通过实验证实。
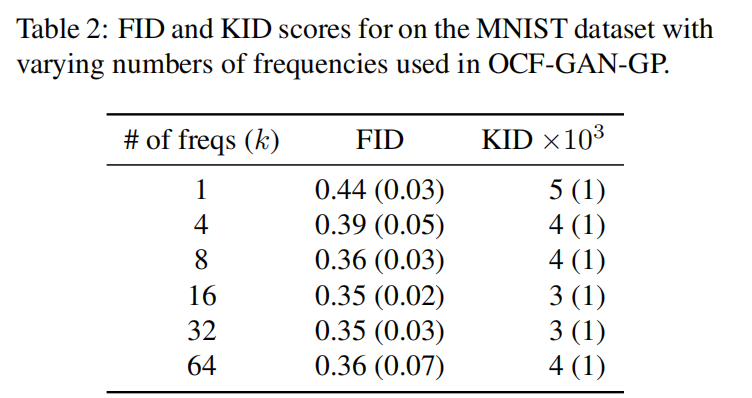
随机频率数量的影响我们进行了实验,研究了从权重分布中采样用于计算ECFD的随机频率数量(k)的影响。我们对我们表现最佳的模型(OCF-GAN-GP)使用了来自集合{1, 4, 8, 16, 32, 64}的不同k值运行了实验。该实验的FID和KID分数如表2所示。如预期的那样,随着k的增加,分数值会提高。然而,即使对于可能的最低频率数量(k = 1),性能也不会严重下降。
6. 讨论与结论
本文提出了一种新颖的基于特征函数的加权距离,用于训练IGM,并展示了所提出的度量具有吸引人的理论特性。实验证明,所提出的模型在四个基准图像数据集上优于MMD-GAN和WGAN变体。我们的结果表明,特征函数为训练IGM提供了一种有效的替代方法。
这项工作为未来的研究开辟了额外的途径。例如,用于训练的经验CFD可能会导致高方差的梯度估计(特别是在采样频率较少的情况下),但在我们的测试中,CFD训练的模型获得了更好的性能分数和更好的收敛性。这一原因应该得到更彻底的探索。虽然我们使用了WGAN-GP提出的梯度惩罚,但没有理由将梯度约束为精确的1。我们相信,对所提出的损失的几何性质进行探索可以改进所提出的方法的梯度正则化器。
除了生成建模之外,诸如MMD之类的双样本检验已用于诸如域适应[25]和域分离[6]等问题。本文提出的优化CFD损失函数可以用作这些问题的替代损失。