近年来,随着数据安全和隐私保护的要求越来越严格,数据孤岛的问题越来越严重,阻碍了AI模型训练的进一步发展,因此隐私计算相关的研究和实践逐渐成为了一个热门的方向。很多机构和学者投入到了隐私计算赛道中。在众多的隐私计算算法中,隐私保护逻辑回归算法是在实践中用的更多的,因为其简单性、鲁棒性、良好的可解释性等优势,它已经被广泛应用于广告点击率预测,信用违约模型和反欺诈等应用中。
前不久数据挖掘的顶级国际会议KDD2021收录了一篇来自阿里巴巴和山东师范大学合作研发的“大规模安全稀疏逻辑回归”算法,文章通过融合同态加密及秘密分享技术,解决了已有算法方案所面临的数据稀疏性问题,因此可以适合于大规模场景。本文将对所提出的方案做简要介绍。

论文地址:https://dl.acm.org/doi/10.1145/3447548.3467210
论文源码:未公布
会议介绍
ACM SIGKDD(Conference on Knowledge Discovery and Data Mining, KDD)是世界数据挖掘领域的最高级别的国际会议,由 ACM(Association of Computing Machinery,计算机学会)的数据挖掘及知识发现专委会(SIGKDD)负责协调筹办,被中国计算机协会荐为A类会议。
自 1995 年以来,KDD 已经以大会的形式连续举办了二十余届全球峰会,作为数据挖掘领域最顶级的学术会议,KDD 大会以论文接收严格闻名,每年的接收率不超过 20%,因此颇受行业关注。
今年KDD发布论文接收结果:本届会议共吸引了 1541 篇论文投递,其中有 238 篇论文被接收,接收率为15.44%,相比 KDD2020 的接收率16.9%继续下降。
逻辑回归模型
在开始介绍算法之前,我们先回顾一下逻辑回归模型。假设某数据集
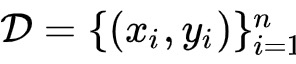
,其中n为样本数量,
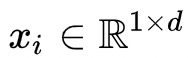
代表第i个样本的特征,d表示特征的维;
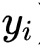
代表第i个样本的标签。逻辑回归的目标是学习一个模型w,用于最小化以下目标函数
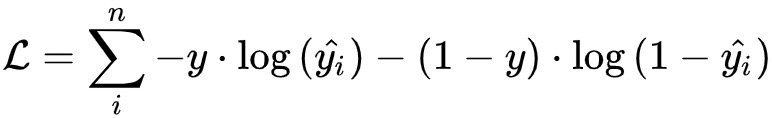
其中,
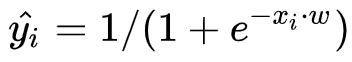
表示第i个样本的预测值。这也正是该模型被称之为逻辑回归的原因。对于线性回归,其预测值
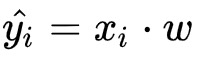
。逻辑回归模型对
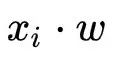
用逻辑函数做了变换,将回归问题转换成了二分类的问题。因此,本章我们所讲述的逻辑回归模型及安全方法可以非常简单的转换为线性回归方法。
逻辑回归模型可以通过最小化以上的目标函数使用梯度下降类的方法迅速求解。通常,用使用mini-batch梯度下降法来做,也就是说,在每次迭代中,不去选一个样本或全部样本,而是随机的选择了一小批量样本用于更新当前模型。具体而言,我们用B表示每个batch,用|B|表示batch size,用
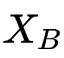
和
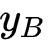
表示当前batch的特征及标签,则神经网络模型会按照以下方式来更新
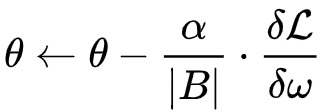
这里,
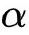
指学习率,
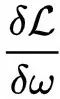
指模型的梯度。对于逻辑回归模型而言
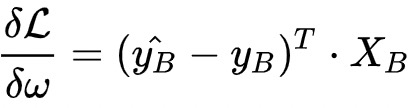
可以看出,在以上的模型更新迭代中,涉及到矩阵乘法
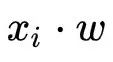
以及逻辑函数的计算。因此,如何高效的计算矩阵简洁及逻辑函数将是实现安全逻辑回归算法的关键。
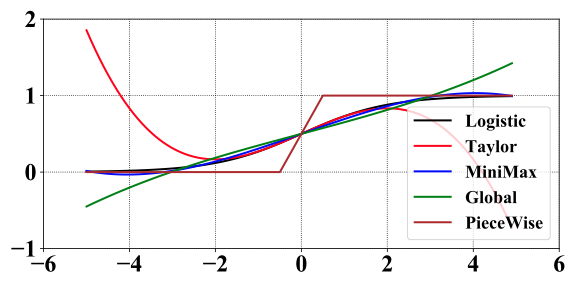
由于逻辑函数(Logistic)是非线性的连续函数,对于密码学技术(比如多方安全计算和同态加密)而言,直接进行精确的计算时间复杂度非常高。因此,已有研究提出了不同的方法来近似逻辑函数,比如泰勒展开,Minimax近似,Global近似,分段函数近似等等。我们将几种近似方法的效果总结在下图中。可以看出,整体而言,Minimax近似方法效果最好,因此我们选择了该方法。在实际的应用中,大家也可以根据不同的场景,选择不同的近似方法。
业界方案
对于隐私计算,或者说隐私保护逻辑回归算法,目前业界主要分为两类:一类是基于多方安全计算,另一类是基于联邦学习。前者具有可证安全的优点,而后者则在模型训练过程中泄露了中间信息。已有的基于多方安全计算的逻辑回归算法更多的是基于秘密分享实现的,而秘密分享技术的本质是将想保护的明文数据通过拆分成若干份随机数,给到不同的计算方来协同计算,以此来达到保护数据安全的目的。但正是这一本质限制了秘密分享算法的用处,即它不能用于很好的解决数据稀疏性问题。
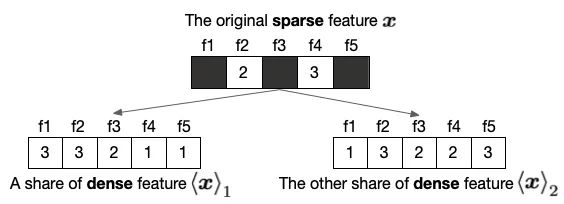
以下图为例,一个原始的稀疏特征,经过秘密分享之后,便变成了稠密特征。而工业的场景中,数据稀疏性问题普遍存在,如果不能很好的解决数据稀疏性问题,就不能很好的将算法扩展到大规模的场景中。
算法模型
从上面逻辑算法的学习过程可以看出,模型训练过程中一个核心的技术是矩阵乘法。已有的安全矩阵乘法通常有两种,一种是基于Beaver’s Triple ,这种做法需要为参与方提前生成随机数三元组(称之为Triplets),这部分需要进行离线训练;另一种不需要提前生成随机数,但牺牲了一些安全性。以上两种秘密分享的做法都不能处理大规模稀疏矩阵的乘法。

为了解决这一问题,作者们提出了一种秘密分享和同态加密的混合协议。在详细介绍该协议之前,先介绍如何在同态加密领域做秘密分享。如上图所示。假设
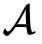
拥有一个同态加密的矩阵

,即它是一个用B的公钥(
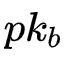
)对矩阵Z加密的结果。如何将该同态加密的矩阵转换成秘密分享的形式呢?
主要可以分为三个步骤:首先,
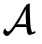
在有限域内生成一个随机数
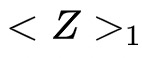
;其次,
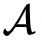
使用同态加密计算另一个分片,并将该加密的分片(
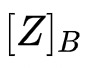
)给到
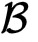
。最后,B使用其私钥(
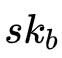
)解密得到另一个分片的明文
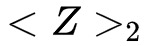
有了同态加密矩阵到秘密分享矩阵的转换协议,我们现在介绍安全的矩阵乘法协议。我们假设有两方,
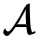
和
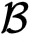
,其中,
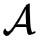
拥有一个高维稀疏矩阵X,而

拥有另一个矩阵Y。同时,
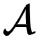
拥有同态加密的公私钥对(
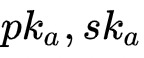
),
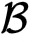
拥有同态加密的公私钥对(
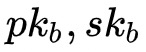
)。
该协议也可以分为三个步骤完成,如下图所示。首先,
使用其公钥(
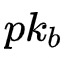
)加密Y并将其给到
。其次,
使用同态加密计算明文矩阵和密文矩阵的乘积。这里只需要用到加法同态加密即可。同时,由于矩阵X是稀疏的,因此,乘法只需要针对非零的元素进行即可。

此外,同态加密过程比较耗时,这里也可以引入分布式计算技术来加速。最后,
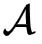
得到加密后的矩阵之后,便可以使用同态加密到秘密分享的转换协议,将其转换到秘密分享域。如此一来,安全矩阵乘法的结果是

和
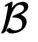
双方各有乘法结果的一个分片。
有了高维稀疏矩阵乘法协议,我们现在介绍如果实现数据垂直切分下的安全逻辑回归算法。这里,为了方便表述,我们假设只有两个参与方,
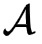
和
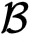
。其中,
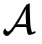
拥有特征
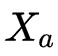
,
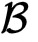
拥有特征
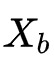
和标签y。整个过程如下图所示。算法的主要思想是

和

首先将各自的模型秘密分享给对方,使得在训练过程中没有任务一方拥有模型的明文,直到模型训练结束,双方才会恢复模型明文。与此同时,
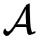
和
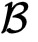
各自维护好特征并秘密分享标签。模型迭代训练过程中,我们使用以上的安全矩阵乘法计算
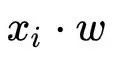
,同时使用Minimax方法来近似逻辑函数,计算预测值的密文,并将其转换为秘密分享域。接着,
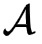
和
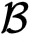
计算误差的分片,并使用安全矩阵乘法计算梯度的分片。最后,他们各自更新自己的模型分片。
以上迭代整个过程中,隐私的数据及模型是以秘密分享或同态加密的形式存在的,直到模型训练结果。如果将整个逻辑回归算法当作是一个安全计算函数,那么该安全逻辑回归算法即是一个多方安全计算的函数。

基于秘密分享和同态加密的逻辑回归算法相对于基于秘密分享的逻辑回归算法的优势:我们记|B|为算法迭代的batch size,记n为样本数,d为双方特征数之和,则该算法的通信复杂度为O(7|B|+2d),也就是过一遍完整的数据通信复杂度为O(7n+2nd/|B|)。相比而言,对基于秘密分享的逻辑回归算法,过一遍完整的数据通信复杂度为O(4nd)。
可以看出,基于秘密分享和同态加密的逻辑回归算法在通信上具有非常大的优势。虽然它引入了同态加密,但这部分的计算开销可以通过分布式计算来解决。因此在多方联合建模的场景下,大部分参与方都是有很强计算能力的商业机构,但机构之间的网络状况不一定有保障,因此如何优化通讯复杂度是算法设计的核心。
01实现
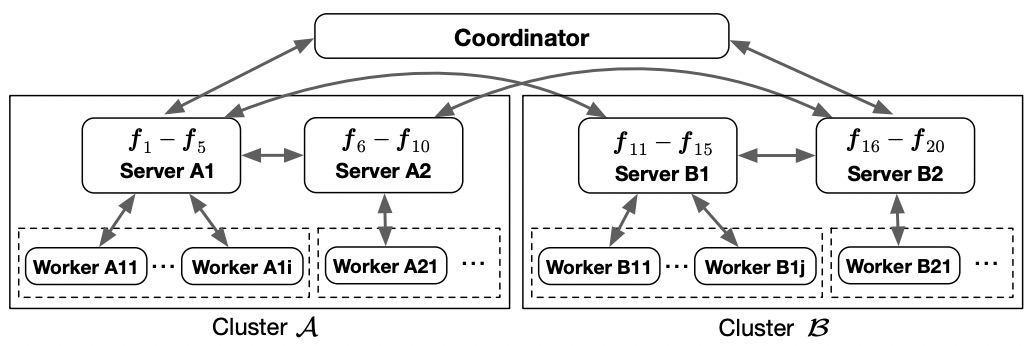
作者们采用了如下的架构来实现该算法。该架构包含了一个协调者(Coordinator),以及两个分布式的计算集群,分别对应两个参与方。该协调者主要控制算法的开始和结束,比如根据迭代轮数等条件。分布式计算集群中的节点又分为Server和Worker。Server主要负责参与双方各自模型的存储,秘密分享相关的计算,以及通信交互。Worker主要负责同态加密相关的计算。之所以这样设计,是因为我们经过分析,发现同态加密计算消耗了大量的时间,因此Server将该部分使用分布式的思想在多个Worker上来计算。
实验
由于基于秘密分享和同态加密的逻辑回归算法在准确率上和基于秘密分享的逻辑回归算法一致,因此,这部分的实验主要对比二者在算法效率上的区别。测试数据包含了100w条样本,特征维度为10w,其中一方拥有 7w特征,另一方拥有3w特征。同态加密的公钥长度设置为2048。
结果如下图,其中,CAESAR为基于秘密分享和同态加密的逻辑回归算法,而SecureML为基于秘密分享的逻辑回归算法。从下图的结果可以看出,CAESAR的算法效率远远高于SecureML,特别是在网络状况不佳和batch size较大的情况下。比如,在网络带宽为10Mbps,batch size为4096的情况下,CAESAR效率为SecureML的近130倍。


此外,作者也分析了几个关键的参数对CAESAR的影响。这些参数包括Worker个数,特征数,batch size,以及网络带宽。可以在下图。可以看出:
- Worker数越多,效率越高,但高于一定值时,将趋于平缓,因为此时计算已经不再是瓶颈 ;
- 模型训练时间跟特征数是线性关系,这一点体现出了算法良好的扩展性;
- batch size越大,算法的效率也越高,这一点进一步证明了我们的时间复杂度分析;
- 网络带宽越大,算法效率也越高,这一点也是显而易见的。
