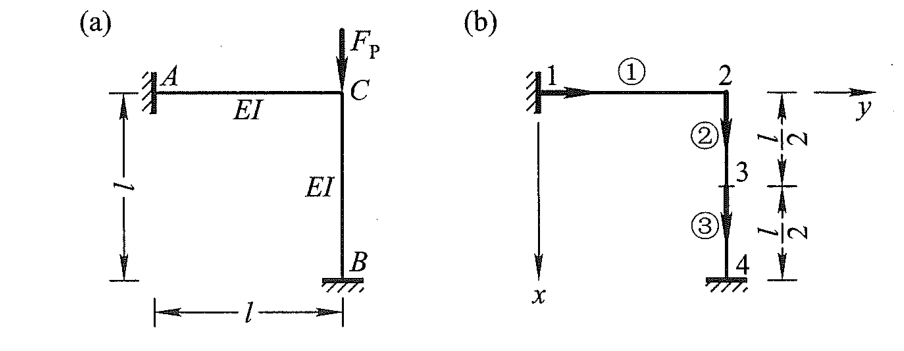
用有限单元法计算图1a所示刚架的临界荷载。相关公式见有限元 | 梁的弹性稳定分析(二)
▲图1
单元划分和结构标识
该刚架仅有
\text{BC}杆受轴向压力作用,失稳时
\text{AC}杆的变形曲线为精确的三次的抛物线。因此,仅将
\text{BC}杆划分为长度相等的两个单元,结构标识如图1b所示。因忽略杆件的轴向变形,当用先处理法分析时仅需列出结点未知位移如下
\boldsymbol{\Delta} = (\theta_2 \quad v_3 \quad \theta_3)^T
组装弹性刚度矩阵和几何刚度矩阵
整体坐标系下,单元①的弹性刚度矩阵放入整体弹性刚度矩阵
\mathbf K =
\frac {EI}{l^3}
\begin{bmatrix}
4l^2 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{bmatrix}
单元②的弹性刚度矩阵放入整体弹性刚度矩阵
\mathbf K =
\frac {EI}{l^3}
\begin{bmatrix}
4l^2+8l^2 & -24l & 4l^2 \\
-24l & 96 & -24l \\
4l^2 & -24l & 8l^2 \\
\end{bmatrix}
单元②的几何刚度矩阵放入整体几何刚度矩阵
\mathbf K_{\sigma} =
\frac {F_P}{60l}
\begin{bmatrix}
4l^2 & -6l & -l^2 \\
-6l & 144 & -6l \\
-l^2 & -6l & 4l^2 \\
\end{bmatrix}
单元③的弹性刚度矩阵放入整体弹性刚度矩阵
\mathbf K =
\frac {EI}{l^3}
\begin{bmatrix}
4l^2+8l^2 & -24l & 4l^2 \\
-24l & 96+96 & -24l+24l \\
4l^2 & -24l+24l & 8l^2+ 8l^2 \\
\end{bmatrix}
单元③的几何刚度矩阵放入整体几何刚度矩阵
\mathbf K_{\sigma} =
\frac {F_P}{60l}
\begin{bmatrix}
4l^2 & -6l & -l^2 \\
-6l & 144+144 & -6l+6l \\
-l^2 & -6l+6l & 4l^2+4l^2 \\
\end{bmatrix}
由
det(\mathbf K - \mathbf K_{\sigma})=0得
\begin{vmatrix}
\frac {EI}{l^3}
\begin{bmatrix}
12l^2 & -24l & 4l^2 \\
-24l & 192 & 0 \\
4l^2 & 0 & 16l^2 \\
\end{bmatrix} -
\frac {F_P}{60l}
\begin{bmatrix}
4l^2 & -6l & -l^2 \\
-6l & 288 & 0 \\
-l^2 & 0 & 8l^2 \\
\end{bmatrix}
\end{vmatrix}
=0
将上式展开可得一个关于轴向力
F_P的三次方程,而方程的最小的根便是临界荷载。
F_P^{cr} = \frac {28.97EI}{l^2}
本问题临界荷载的精确值为
F_P^{cr} = \frac {28.4EI}{l^2},上述有限元解比精确值偏高约2%,原因是假定了单元的位移函数相当于增加了无形的约束,从而增加了结构的刚度。
采用上述算法得不到屈曲模态,需要改进。