计算机初级选手的成长历程——操作符详解（3）

大家好，很高兴又和大家见面了！！！今天咱们要对操作符的内容进行一个收尾。在前两篇的内容中我们详细介绍了10类操作符及其相关的知识点，我们学习这些操作符的目标最终还是为了对表达式进行求值。

在学习C语言的过程中，我们在做习题的时候，或者在写代码的时候，会遇到比较简单的表达式如a+b、c^d这种只有一个操作符的表达式；

我们还会遇到比较复杂的表达式如++a*b^c>>2这种有多个操作符的表达式，对于这些表达式我们又应该如何求值呢？下面我们就来介绍一下如何利用这些操作符对表达式求值；

表达式求值

对表达式的求值内容，我们分为两个区块介绍，一个是简单的表达式求值，一个是复杂的表达式求值。

对于简答的表达式，我们可能会遇到的问题就是不同类型的操作对象进行运算，如：

代码语言：javascript

复制

//表达式求值
int main()
{
	char a = 'a';
	short b = 1;
	int c = 2;
	float d = 3.14f;
	double e = 2.58;
	a + b + c + d + e;
	return 0;
}

在这种情况下，五个变量的类型都不相同，对于表达式a + b + c + d + e的值，我们又应该如何计算呢？

对于上述这种多类型的表达式求值，我们在对其求值的过程中需要将它们转化成其它的类型。在前面我们有介绍过一种类型转换的方式，通过强制类型转换操作符进行的类型转换，接下来我们来介绍另一种转换方式——隐式类型转换；

隐式类型转换

在介绍隐式类型转换前，我们先要对这个转换有一个初步的理解才行。那什么是隐式类型转换呢？

我的理解就是字面意思：隐——隐藏、隐蔽——偷偷摸摸的，不易察觉的，那隐式类型转换就是让人无法察觉的进行类型转换；

那什么情况下才会进行隐式类型转换呢？

这里有两种情况：

一种是当操作数的类型所占空间大小小于一个整型所占空间大小时，会将操作数转换成整型后再进行运算，这种叫做整型提升；

另一种是当操作数在进行运算时，它们的类型都不相同，并且类型所占空间大小大于或等于一个整型所占空间大小时，其中的一个操作数将转化为另一个操作数的类型，这种叫做算术转换；

下面我们来一一介绍这两种转换的方式；

整型提升

什么是整型提升？

C的整型算术运算总是至少以缺省整型类型的精度来进行的。

为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

光看这两句话，我们都不太好理解什么是整型提升，下面我们来了解一下为什么要整型提升？整型提升的意义是什么？

整型提升的意义

表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度，同时也是CPU的通用寄存器的长度。因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

简单来说就是在进行整型运算时，因为这个运算是在CPU内进行的，但是CPU内负责整型运算的运算器它的操作数的字节长度一般是一个int类型的字节长度；

当操作数的字节长度小于一个int类型的字节长度时，这个整型运算器是无法正常工作的。

为了让这个运算器正常工作，这时我们需要将char和short这两种数据类型的操作数先转化成int类型，再进行整型计算，这样这个运算器就能正常工作了。

现在我们再来理解什么是整型提升，所谓的整型提升其实就是将char和short这两种类型的操作数转换成int类型的过程。

下面我们来通过例子进一步理解什么是整型提升：

代码语言：javascript

复制

//表达式求值
int main()
{
	char a = 1, b = 2, c = a + b;
	printf("%d\n", c);
	a = 1, b = 126, c = a + b;
	printf("%d\n", c);
	a = 1, b = 127, c = a + b;
	printf("%d\n", c);
	return 0;
}

我们来看一下这个代码，现在我们对字符类型的变量a、b分别进行了3次赋值——1,2、1,126、1,127，大家觉得如果我直接以整型打印，结果会是多少？

下面我们来看一下运行结果：

这个结果跟各位的预期是一样的吗？下面我就来解释一下为什么会出现这个结果；

简单的理解就是，字符在进行整型运算时，只是将字节大小提升成了int的字节大小后，再按正常的int类型进行运算，所以我们可以看到当a=1,b=2或者a=1,b=126时c的结果就是两数之和；

但是如果仅仅只是这种提升方式的话为什么在第三种情况下，结果会变成c=-128呢？接下来我们来学习一下这个整型提升是如何进行的；

如何进行整型提升？

整型提升是按照变量的数据类型的符号位来提升的：

负数的整型提升因为符号位为1，所以高位补充的也是1；正数的整型提升因为符号位为0，所以高位补充的也是0；

上面介绍的是整型提升的规则，简单的理解就是

当符号位为1时，提升的比特位补充的内容都是1；当符号位为0时，提升的比特位补充的内容都是0；

经过前面的学习，我们知道对于有符号数来说，最高位就是它们的符号位，对于有符号的char和short类型的数来说同样适用。

接下来根据这个提升规则我们来理解一下为什么在上述代码的第三种情况下结果会发生变化；

我们知道对于有符号的数字1来说，它的原码/反码/补码都为：

00000000000000000000000000000001

那对于有符号的数字127来说，它的原码/反码/补码又是多少呢？我们借助程序员计算机来查看一下，步骤如下所示；

1.大家可以使用快捷键win+r来打开Windows的运行窗口，并在窗口中输入clar打开计算器：

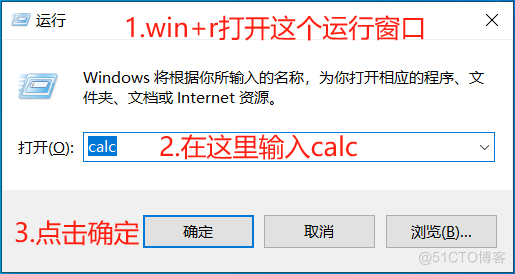
2.进入计算器后将计算器调整成程序员模式：

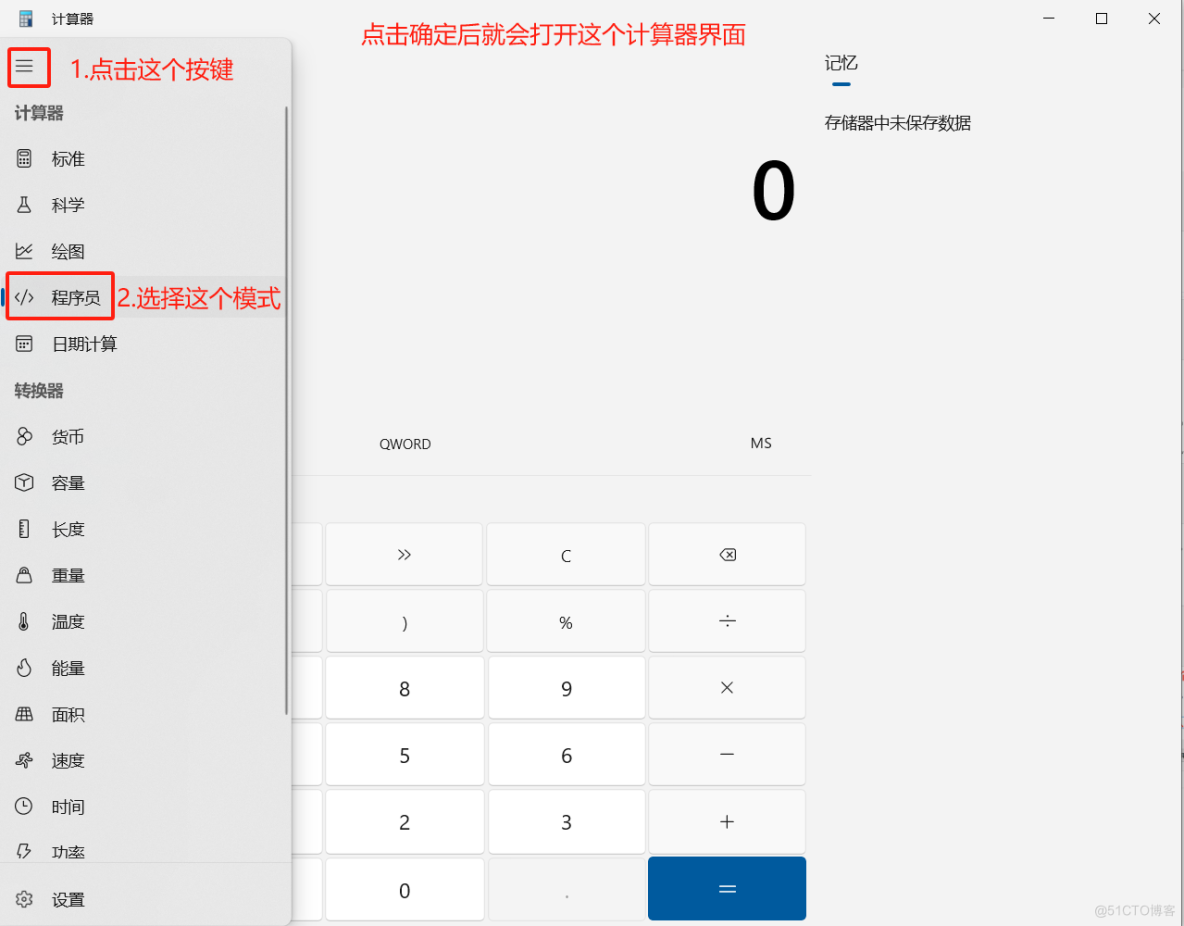
3.在十进制模式下输入127来查看127的二进制形式：

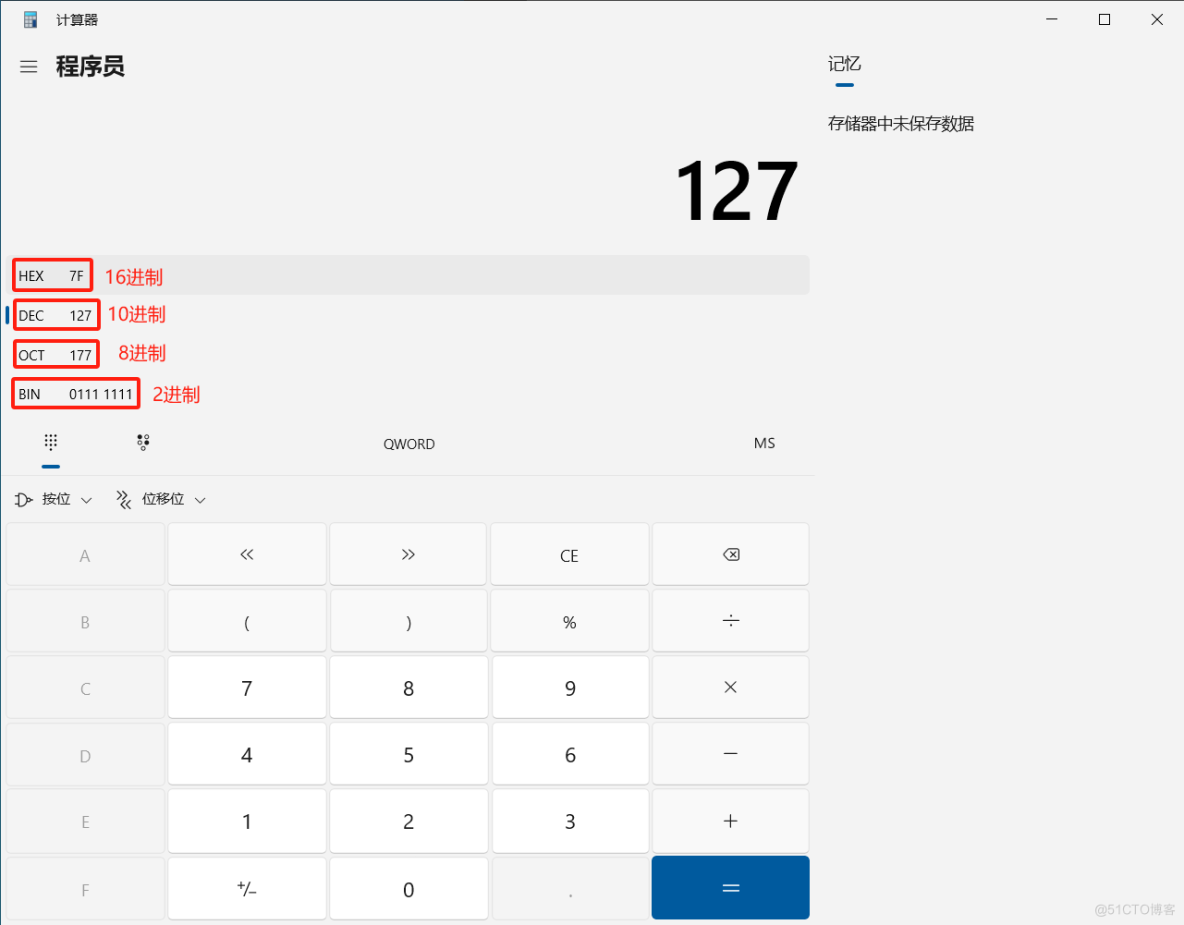
可以看到127的二进制形式为01111111，它实际在计算机内存中的二进制序列为：

00000000000000000000000001111111

这个二进制序列也就是有符号整数127的原码/反码/补码。现在我们已经知道了1和127的补码，那对于字符a和b来说，它们作为字符类型的变量是如何存储这个内容的呢？这就是我们要介绍的一个内容——截断；

截断

对于截断我们可以简单的理解为就是将高字节位的内容存存储在低字节的变量中的一个转换过程；

那它的截断规则又是什么呢？

我们在前面看到了整型提升的规则，简单的概括出来就是在高位上补充缺少的字节，截断刚好与整型提升相反，它是保留低位的字节，去掉高位多出来的字节，对于数字1和127来说，它们的截断过程如下如所示：

在截断完成后a的二进制序列为00000001，b的二进制序列为01111111；

接下来我们需要让a和b完成整型运算，如何完成呢？下面我们就来探讨一下这个过程；

在前面的介绍中我们有提到，在进行整型运算时，当运算的操作数的字节位不足一个整型字节位时，我们需要进行整型提升，整型提升是按照操作数的符号位来提升的，也就是说，此时的a和b需要进行整型提升，那它们提升的过程如下：

对于提升后的a和b再进行相加我们就很熟悉了很容易的到结果为：

00000000000000000000000010000000

现在我们要将这个结果存放在字符c内，此时它需要发生截断，最后我们要将c以整型的形式打印出来，它需要进行整型提升，这个截断和提升的过程如图所示：

此时我们可以看到通过这一系列操作后，c的二进制序列的符号位由0变为了1，也就是说此时的c是一个负数，那负数的原码我们需要进行补码->反码->原码的一系列转换，转换过程如下：

这样我们就得到了c=-128。

小结

当在进行整型运算时，如果操作数的字节长度不足一个整型的字节长度，那么在运算的过程中，我们需要完成一下步骤：

将整型数存放在变量中，这个过程会发生截断，将高位多出的字节去掉，低位保留相应的字节长度；
将变量进行整型运算，这个过程会发生整型提升，由当前二进制序列的最高位的数字来在高位补充缺失的字节：

如果此时最高位为0，则高位补充字节内容为0；如果此时最高位为1，则高位补充字节内容为1；

将运算后的数存放在变量中，如果这个存放的变量字节长度不足整型长度，会发生截断；

对于char类型来说，它能存储的整型值的范围是-2^7~2^7-1也就是-128~127，而且我们在手算时可以按照下面的规则进行运算：

当正整数之和小于等于127时，运算结果为两数相加的值；

当正整数之和大于127时，具体的值需要进行整型提升与截断才能最终确定其值；

两数之和的值为一个以0-256为一个周期的周期函数，图像如下所示：

以上就是整型提升的全部内容，这是对于char和short这个两个类型而言，接下来我们来介绍另一种转换方式；

算术转换

我们先想象一下一种情况——在某个操作符的各个操作数属于不同类型时，除非其中一个操作数转换为另一个操作数的类型，否则操作就无法进行。

在这个情况中的操作符可不是指算术操作符，还可能是其它的操作符，这里我们方便起见，以最开始的例子来说明：

代码语言：javascript

复制

//表达式求值
int main()
{
	char a = 'a';
	short b = 1;
	int c = 2;
	float d = 3.14f;
	double e = 2.58;
	a + b + c + d + e;
	return 0;
}

在这个例子中我们可以看到这里的五个变量的类型各不相同，对于a、b两个变量要进行运算时，我们知道了应该先进行整型提升，再进行整数运算，那对于c、d、e这个三个已经满足了一个整型字节大小的不同类型时，我们又应该如何执行呢？

在这种情况下，就需要用到我们现在要介绍的算术转换的相关知识了。

什么是算术转换？

所谓的算术转换我们可以简单的理解为是当我们对不同类型的操作数进行运算时，其中一个操作数会无条件转换成另一个操作数的类型的这个过程。

进行算术转换的操作对象是字节大小满足一个整型字节大小的操作对象；

对于不满足整型字节大小的对象，需要先进行整型提升，再进行算术转换。

如何进行算术转换？

我们先来看一张数据类型的名次表：

名次	数据类型
1	long double
2	double
3	float
4	unsigned long int
5	long int
6	unsigned int
7	int

在表中我们可以看到，int的名次最低，long double的名次最高。这种数据类型的层次体系称为寻常算术转换。

当我们的操作数的数据类型不同，且一个操作数的数据类型排名低于另一个操作数的数据类型排名时，类型排名较低的操作数会无条件转换为另一个操作数的类型，然后再执行运算。

也就是说当int与float这两个数据类型的操作数进行运算时，int类型的操作数会先无条件转换成float类型，然后再进行运算；

同理float与double这两个数据类型也是一样的情况，float会无条件转换成double类型，然后再进行运算；

在了解了这些知识点后，我们再来手算一下刚刚的例子，

由字符a的ASCII码值为97，这些值加起来为105.72，值的类型应该为double类型，下面我们来看一下运行结果：

从这个运算结果中我们可以看到，它这里的精度出现了点问题，但是大体上还是这个值。会出现这个情况是因为在进行隐式转换的时候整型数转换成浮点数时，会出现精度丢失的问题，解决也很简单，如下图所示：

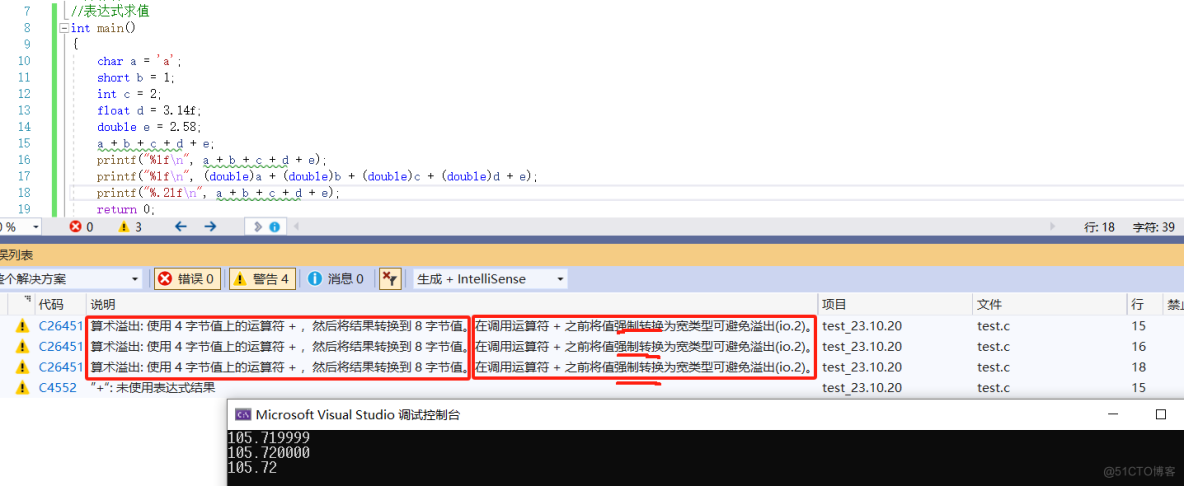
在运行时程序会提示我们像这样操作导致算术溢出了，如果要解决的话，需要在调用运算符前先将值强制转化成宽类型，这样就避免了溢出的问题。

如上图所示，在第二次打印时我们就将不是double类型的对象都进行了强制转化，所以最终的结果为105.720000；

还有一种解决办法就是，它既然丢失了精度，我们直接给它精度也就是通过%.*lf这种格式来打印，这里的*代表的是精度。我们在赋值时给d和e赋值的是两位小数，所以这里我通过%.2lf这种格式来打印，也能得到正常的值105.72。

小结

在进行运算时，两个操作对象中数据类型名次较低的操作对象会转换另一个操作对象的数据类型，再进行运算；

在整型值转换成浮点型时，会出现精度丢失的问题，我们有两种解决方式：

可以通过在打印时以%.lf的格式给结果相应的精度来进行打印；或者避开隐式类型转换，使用强制类型转换直接将整型强制转换成浮点型；

介绍完了隐式类型转换，我们会发现，刚刚我们遇到的问题都是操作符相同的情况下，如果在操作符不同的情况下我们又应该如何进行表达式求值呢？接下来我们就来介绍一下相关知识点；

操作符的属性

对于像最开始咱们举的例子++a*b^c>>2这种复杂的表达式来说，求值取决于三个因素：

操作符的优先级
操作符的结合性
是否控制求值顺序

两个相邻的操作符先执行哪个？取决于它们的优先级，如果优先级相同，则取决于它们的结合性。

优先级

操作符的优先级是指如果一个表达式包含多个运算符，哪个运算符应该优先执行。

下面我们来看一下各个操作符的优先级：

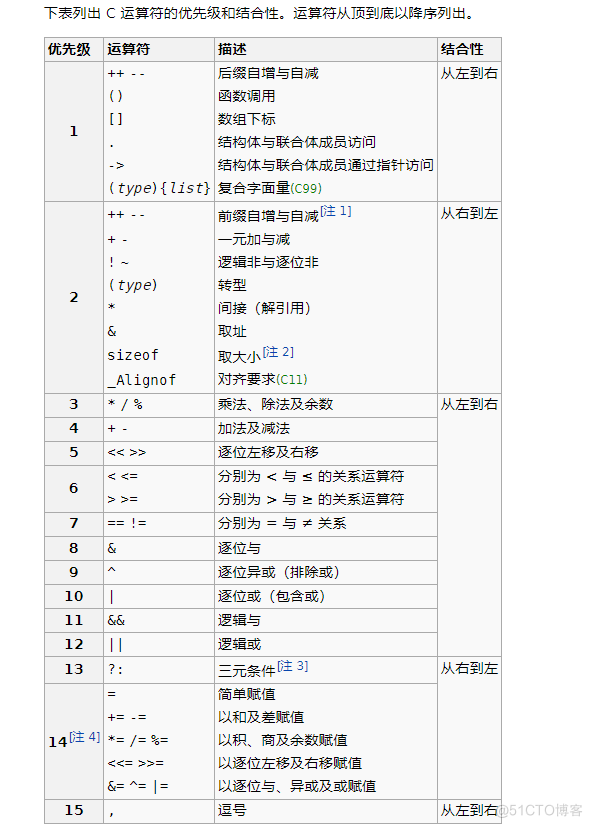
资料参考：https://zh.cppreference.com/w/c/language/operator_precedence

知道了操作符的优先级，那对于例子中的前置++、乘法、按位异或、和右移操作符的优先级我们可以对照上表进行排序：

优先级	操作符
1	前置++(++a)
2	乘法((++a)*b)
3	右移(c>>2)
4	按位异或((++a)*b)^(c>>2)

现在我们就解决了当操作符优先级不同时的问题，那如果操作符优先级相同呢？这就是我们要介绍的另一个属性——结合性；

结合性

如果两个运算符优先级相同时，我们需要根据结合性来决定执行顺序。

所谓的结合性我们可以简单的理解为操作符的运算方向，操作符在运算时要么是从左到右运算，要么是从右到左运算；

从左到右运算的操作符，我们称它的结合性为左结合，从右到左运算的操作符，我们称它的结合性为右结合；

大部分的操作符都是左结合，比如我们在介绍隐式类型转换时，用到的操作符是加法，查表可知它的结合性是左结合，所以我们在运算时是从左边往右边计算，这也符合我们数学中加法的运算顺序；

少部分的运算符是右结合，比如赋值语句a=2这时的运算是从右往左执行，所以它的执行逻辑是把2赋值给a。

小结

我们在进行表达式计算时，首先判断操作符的优先级，在优先级相同的情况下，我们再判断操作符的结合性，以此来决定计算顺序；

对于三目操作符、逻辑或、逻辑与以及逗号这四个操作符来说，它们在进行运算时会控制求值顺序；

如三目操作符会根据表达式1的值的不同而进行不同顺序的求值；逻辑或在左操左对象为真时，不再计算右操作对象；逻辑与在做操作对象为假时，不再计算右操作对象；逗号表达式的值是最右边表达式的值；

运算符的优先级顺序很多，下⾯是部分运算符的优先级顺序（按照优先级从⾼到低排列），建议⼤概

记住这些操作符的优先级就⾏，其他操作符在使⽤的时候查看上⾯表格就可以了。

• 圆括号（ () ）

• ⾃增运算符（ ++ ），⾃减运算符（ -- ）

• 单⽬运算符（ + 和 - ）

• 乘法（ * ），除法（ / ）

• 加法（ + ），减法（ - ）

• 关系运算符（ < 、 > 等）

• 赋值运算符（ = ）

由于圆括号的优先级最⾼，可以使⽤它改变其他运算符的优先级。

介绍完这两个属性，我们来看看几个表达式；

问题表达式解析

表达式一——a * b + c * d + e * f

对于这个表达式，我们可以看到它是由两个操作符——+和*组成的表达式，按优先级来说，计算机在计算时只能根据*的优先级比+高，从而保证乘法的计算比加法早，但是优先级并不能保证第三个乘法比第一个加法早执行，因此，计算机在计算这个表达式的时候可能的顺序是：

顺序1
计算步骤	执行操作
1	a*b
2	c*d
3	ab+cd
4	e*f
5	ab+cd+e*f
顺序2
计算步骤	执行操作
1	a*b
2	c*d
3	e*f
4	ab+cd
5	ab+cd+e*f

像这样的话对于有些表达式求值，在结果上就会产生出入；

表达式二——c + --c

这个表达式同上，我们只能根据操作符的优先级来确定前置--在+之前进行运算，但是无法确定+的左操作数的获取是在前置--之前还是之后，比如：

代码语言：javascript

复制

int c = 1;
	c = c + --c;

如果+的取值在前置--前，那么结果就为1，如果+的取值在前置--后，那么结果就为0；因此我们并不能准确判断表达是的结果，此时的表达式就是有歧义的表达式；

表达式三——i=i-- - --i * ( i = -3 ) * i++ + ++i

代码如下：

代码语言：javascript

复制

//问题表达式3
int main()
{
	int i = 10;
	i = i-- - --i * (i = -3) * i++ + ++i;
	printf("i = %d\n", i);
	return 0;
}

对于这个代码，在不同的编译器下的执行结果为：

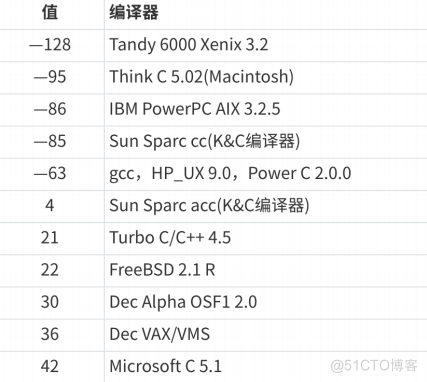
像这种情况，我们又应该以哪个编译器的结果为准呢？所以对于这个表达式的结果也是有歧义的；

表达式四——answer = fun() - fun() * fun()

代码如下：

代码语言：javascript

复制

//问题表达式4
int fun()
{
	static int count = 1;
	return ++count;
}
int main()
{
	int answer;
	answer = fun() - fun() * fun();
	printf("%d\n", answer);//输出多少？
	return 0;
}

对于这个表达式，我们能确定的只有函数调用在乘法前面，乘法运算在减法的前面，但是我们并不能确定哪一个函数先进行调用，那就可能出现以下的几种情况：

计算步骤	执行顺序
1	fun()=2
2	fun()=3
3	fun()=4
4	fun()*fun()
5	fun()-fun()*fun()
情况1
函数调用顺序	表达式的值
从左到右依次调用	2-3*4=-10
情况1
函数调用顺序	表达式的值
从乘法左边到右最后到减法左边依次调用	4-2*3=-2

像这种因为调用顺序不同导致值有歧义的表达式也是有问题的；

表达式五——ret = (++i) + (++i) + (++i)

代码如下：

代码语言：javascript

复制

//表达式5
#include <stdio.h>
int main()
{
 int i = 1;
 int ret = (++i) + (++i) + (++i);
 printf("%d\n", ret);
 printf("%d\n", i);
 return 0;
}

对于这个表达式的形式是不是与第一个表达式的形式类似啊，都是由两个优先级不同的操作符组成，而且都不能确定优先级高的第三个操作符和优先级低的第一个操作符的运算顺序，但是这里与第一个表达式不同的地方在于，前置++的结合性是从右到左进行，而加法的结合性是从左到右进行，此时就会出现一下几种情况：

顺序1
计算步骤	执行操作	实际运算过程
1	++i=2	++i + ++i + ++i
2	++i=3	++i + ++i + 2
3	++i=4	++i + 3 + 3
4	4+4=8	4 + 4 + 4
5	8+=12	8+4
顺序2
计算步骤	执行操作	实际运算过程
1	++i=2	++i + ++i + ++i
2	++i=3	++i + ++i + 2
3	3+3=6	++i + 3 + 3
4	++i=4	++i + 6
5	4+6=10	4+6

由此我们可以判断，这个表达式也是一个问题表达式；

小结

即使操作符有各自的优先级和结合性，如果我们不能通过这两个属性来使表达式具有唯一确定的计算途径，那这个表达式就是一个有风险的表达式，建议不要写出这种表达式；

为了保证计算途径的唯一性，我们可以通过圆括号将先执行的表达式给括起来，拿表达式五来说，我们可以像这样处理：

++i + (++i + ++i)，在这种情况下我们就能根据优先级和结合性判断，先执行后面的两个前置++，再将经过两次自增后的结果相加，之后再进行前置++，最后将自增后的值与前一次的和相加，就能得到值为10，这样我们的表达式就没有歧义了。

总结

这一篇我们给操作符的内容进行了收尾，详细讲解了操作符在表达式中的使用，希望今天的内容对各位在操作符的使用与表达式的求值这一块内容上有帮助。接下来随着学习的深入，我会继续给大家分享我在学习过程中的感受，感谢各位的翻阅，咱们下一篇再见！